Download video slide

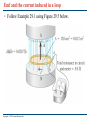
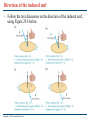
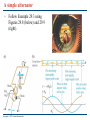
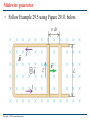
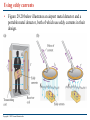
Chapter 29
Electromagnetic
Induction
PowerPoint® Lectures for
University Physics, Thirteenth Edition
– Hugh D. Young and Roger A. Freedman
Lectures by Wayne Anderson
Copyright © 2012 Pearson Education Inc.
Goals for Chapter 29
• To examine experimental evidence that a changing
magnetic field induces an emf
• To learn how Faraday’s law relates the induced emf to
the change in flux
• To determine the direction of an induced emf
• To calculate the emf induced by a moving conductor
• To learn how a changing magnetic flux generates an
electric field
• To study the four fundamental equations that describe
electricity and magnetism
Copyright © 2012 Pearson Education Inc.
Introduction
• How is a credit card reader
related to magnetism?
• Energy conversion makes
use of electromagnetic
induction.
• Faraday’s law and Lenz’s
law tell us about induced
currents.
• Maxwell’s equations
describe the behavior of
electric and magnetic fields
in any situation.
Copyright © 2012 Pearson Education Inc.
Induced current
• A changing magnetic flux causes an induced current. See Figure
29.1 below.
• The induced emf is the corresponding emf causing the current.
Copyright © 2012 Pearson Education Inc.
Magnetic flux through an area element
• Figure 29.3 below shows how to calculate the magnetic
flux through an element of area.
Copyright © 2012 Pearson Education Inc.
Faraday’s law
• The flux depends on the orientation of the surface with respect
to the magnetic field. See Figure 29.4 below.
• Faraday’s law: The induced emf in a closed loop equals the
negative of the time rate of change of magnetic flux through the
loop, or  = –dB/dt.
Copyright © 2012 Pearson Education Inc.
Emf and the current induced in a loop
• Follow Example 29.1 using Figure 29.5 below.
Copyright © 2012 Pearson Education Inc.
Direction of the induced emf
• Follow the text discussion on the direction of the induced emf,
using Figure 29.6 below.
Copyright © 2012 Pearson Education Inc.
Magnitude and direction of an induced emf
• Read Problem-Solving Strategy 29.1.
• Follow Example 29.2 using Figure 29.7 below.
Copyright © 2012 Pearson Education Inc.
A simple alternator
• Follow Example 29.3 using
Figures 29.8 (below) and 29.9
(right).
Copyright © 2012 Pearson Education Inc.
DC generator and back emf in a motor
• Follow Example 29.4 using Figure 29.10 below.
Copyright © 2012 Pearson Education Inc.
Slidewire generator
• Follow Example 29.5 using Figure 29.11 below.
Copyright © 2012 Pearson Education Inc.
Work and power in the slidewire generator
• Follow Example 29.6 using Figure 29.12 below.
Copyright © 2012 Pearson Education Inc.
Lenz’s law
• Lenz’s law: The direction of any magnetic induction
effect is such as to oppose the cause of the effect.
• Follow Conceptual Example 29.7.
Copyright © 2012 Pearson Education Inc.
Lenz’s law and the direction of induced current
• Follow Example 29.8
using Figures 29.13
(right) and 29.14 (below).
Copyright © 2012 Pearson Education Inc.
Motional electromotive force
• The motional electromotive force across the ends of a rod
moving perpendicular to a magnetic field is  = vBL. Figure
29.15 below shows the direction of the induced current.
• Follow the general form of motional emf in the text.
Copyright © 2012 Pearson Education Inc.
A slidewire generator and a dynamo
• Follow Example 29.9 for the slidewire generator.
• Follow Example 29.10 for the Faraday disk dynamo, using Figure
29.16 below.
Copyright © 2012 Pearson Education Inc.
Induced electric fields
• Changing magnetic flux
causes an induced electric
field.
• See Figure 29.17 at the right
to see the induced electric
field for a solenoid.
• Follow the text discussion for
Faraday’s law restated in
terms of the induced electric
field.
• Follow Example 29.11 using
Figure 29.17.
Copyright © 2012 Pearson Education Inc.
Eddy currents
• Follow the text
discussion of eddy
currents, using Figure
29.19 at the right.
Copyright © 2012 Pearson Education Inc.
Using eddy currents
• Figure 29.20 below illustrates an airport metal detector and a
portable metal detector, both of which use eddy currents in their
design.
Copyright © 2012 Pearson Education Inc.
Displacement current
• Follow the text discussion displacement current using Figures
29.21 and 29.22 below.
Copyright © 2012 Pearson Education Inc.
Maxwell’s equations
• Maxwell’s equations consist of
 Gauss’s law for the electric field
 Gauss’s law for the magnetic field
 Ampere’s law
 Faraday’s law.
• Follow the text discussion for the mathematical form
of these four fundamental laws.
Copyright © 2012 Pearson Education Inc.
Superconductivity
• When a superconductor is
cooled below its critical
temperature, it loses all
electrical resistance.
• Follow the text discussion
using Figures 29.23 (below)
and 29.24 (right).
Copyright © 2012 Pearson Education Inc.