Download Document

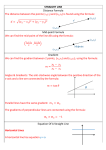
EQUATION
A
rule describing relationships between
variables
 y = F (x)
reads y is a function of x
i.e. y depends upon x
2
FORMULAE
- Enables us to calculate the value of one variable
form the value(s) of one / more variable(s)
Example:
 In
y = F (x)
y is the dependent variable
x is the independent variable
 Examples
Exam success (y) depends upon IQ (x)
Illness (y) depends upon age (x)
Lifetime income (y) depends upon educational
qualifications (x)
4
TRY!!
1) If 47x + 256 = 52x. Find x?
2) If
1
=
5
. Find x?
3x + 4
2.7x – 2
3) Rearrange x = (12y – 10)2 in y term of x
4) Rearrange 4(2y – 3) + 2(x +4)=0 to get
an expression for x in terms of y.
5
 E.g.
y = mx+ c
 Highest power (exponent) of the independent
variable (x) is one
 This gives a straight line graph
6
y = mx + c
y
c
)m
0
x
7
In the previous graph
 c = intercept, i.e. the value of y when x = 0
m
= gradient, i.e. the slope of the straight
line
8
 Slope
of a straight line (or curve at a point)
 Positive gradients: slope up from left to right
(+ sign)
 Negative gradients: slope down from left to
right (-)
10
Gradient = vertical distance
horizontal distance
(y2 – y1)
(x2 – x1)
4cm
2c m
5 cm
5 cm
a)
b)
Gradient = 2/5 = 0.4 (+)
Gradient = 4/5 = 0.8 (-)
11
TRY!!
1) This is 2 point in straight-line graph:
A (x=2, y=11) & B (x=4, y=21)
Find the gradient.
2) Y= 4 -2x, the gradient is?
3) A company manufactures a product. The
variable cost per unit is $5 and total fixed costs
are $9.
a. Find an expression for total cost(c) in terms of q,
the quantity produced
b. Determine the total costs if 100 units are produced
12
For the time being, we shall deal only with
quadratic equations that can be factored
(factorised).
 Using the fact that a product is zero if any of its
factors is zero we follow these steps:

(i) Bring all terms to the left and simplify, leaving
zero on the right side.
(ii) Factorise the quadratic expression
(iii) Set each factor equal to zero
(iv) Solve the resulting linear equations
(v) Check the solutions in the original equation
13
14
Application in business:
 Need to find the price at which supply equals
demand
 Break-even point
The idea:
Eliminate either x or y variable, whether by
addition or subtraction, so that we are left
with one equation with unknown variable.
15
 Values
of x and y which solve both equations
at the same time
 Graph solution – where lines (represent
equations) intersect
16
•
Example – solve y = 3x – 1
and
•
Plot the line for each equation on a graph
Use the values x = 0, 1, 2 and 3
Find the value of x and y where the two lines
intersect
•
•
17
y
9
y=3x-1
5.7
x
0
-1
2.2
y   32 x  9
18
 y=
3x + 16,
 2y = x + 72
19