Download Document

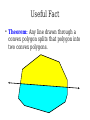
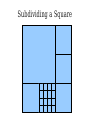
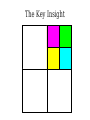
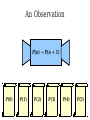
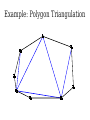
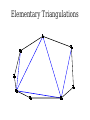
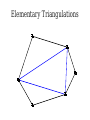
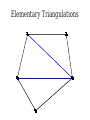
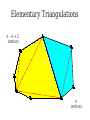
Mathematical Induction
Part Two
Announcements
●
●
Problem Set 1 due Friday, October 4 at
the start of class.
Problem Set 1 checkpoints graded, will
be returned at end of lecture.
●
Afterwards, will be available in the filing
cabinets in the Gates Open Area near the
submissions box.
The principle of mathematical induction
states that if for some P(n) the following hold:
P(0) is true
If it starts
true…
and
…and it stays
true…
For any n ∈ ℕ, we have P(n) → P(n + 1)
then
…then it's
always true.
For any n ∈ ℕ, P(n) is true.
n−1
Theorem: For any natural number n,
∑ 2i =2n−1
i=0
Proof: By induction. Let P(n) be
n−1
P(n) ≡ ∑ 2i =2n −1
i=0
For our base case, we need to show P(0) is true, meaning that
−1
∑ 2i =20−1
i=0
Since 20 – 1 = 0 and the left-hand side is the empty sum, P(0)
holds.
For the inductive step, assume that for some n ∈ ℕ, that P(n)
n−1
holds, so
∑ 2i =2n−1
i=0
We need to show that P(n + 1) holds, meaning that
n
∑ 2i =2n+ 1−1
i=0
To see this, note that
n
n−1
i=0
i=0
∑ 2i =(∑ 2i )+2 n =2n −1+ 2n=2(2n )−1=2n+ 1−1
Thus P(n + 1) holds, completing the induction. ■
Induction in Practice
●
●
●
Typically, a proof by induction will not
explicitly state P(n).
Rather, the proof will describe P(n) implicitly
and leave it to the reader to fill in the details.
Provided that there is sufficient detail to
determine
●
what P(n) is,
●
that P(0) is true, and that
●
whenever P(n) is true, P(n + 1) is true,
the proof is usually valid.
n−1
Theorem: For any natural number n, ∑ 2i =2n −1
i=0
Proof: By induction on n. For our base case, if n = 0, note that
−1
∑ 2i =0=20 −1
i=0
and the theorem is true for 0.
For the inductive step, assume that for some n the theorem is
true. Then we have that
n
n−1
i=0
i =0
∑ 2i =∑ i + 2n=2 n−1+2 n=2(2 n)−1=2 n+1−1
so the theorem is true for n + 1, completing the induction. ■
Variations on Induction: Starting Later
Induction Starting at 0
●
To prove that P(n) is true for all natural
numbers greater than or equal to 0:
●
●
●
Show that P(0) is true.
Show that for any n ≥ 0, that
P(n) → P(n + 1).
Conclude P(n) holds for all natural numbers
greater than or equal to 0.
Induction Starting at k
●
To prove that P(n) is true for all natural
numbers greater than or equal to k:
●
●
●
●
Show that P(k) is true.
Show that for any n ≥ k, that
P(n) → P(n + 1).
Conclude P(n) holds for all natural numbers
greater than or equal to k.
Pretty much identical to before, except
that the induction begins at a later point.
Convex Polygons
●
A convex polygon is a polygon where,
for any two points in or on the polygon,
the line between those points is
contained within the polygon.
Useful Fact
●
Theorem: Any line drawn through a
convex polygon splits that polygon into
two convex polygons.
Summing Angles
●
●
Interesting fact: the sum of the angles in
a convex polygon depends only on the
number of vertices in the polygon, not
the shape of that polygon.
Theorem: For any convex polygon with n
vertices, the sum of the angles in that
polygon is (n – 2) · 180°.
●
Angles in a triangle add up to 180°.
●
Angles in a quadrilateral add up to 360°.
●
Angles in a pentagon add up to 540°.
Theorem: The sum of the angles in any convex polygon with n vertices
is (n – 2) · 180°.
Proof: By induction. Let P(n) be “all convex polygons with n vertices
have angles that sum to (n – 2) · 180°.” We will prove P(n) holds for
all n ∈ ℕ where n ≥ 3. As a base case, we prove P(3): the sum of the
angles in any convex polygon with three vertices is 180°. Any such
polygon is a triangle, so its angles sum to 180°.
For the inductive step, assume for some n ≥ 3 that P(n) holds and all
convex polygons with n vertices have angles that sum to (n–2) · 180°.
We prove P(n+1), that the sum of the angles in any convex polygon
with n+1 vertices is (n–1) · 180°. Let A be an arbitrary convex
polygon with n+1 vertices. Take any three consecutive vertices in A
and draw a line from the first to the third, as shown here:
A
B
C
The sum of the angles in A is equal to the sum of the angles in
triangle B (180°) and the sum of the angles in convex polygon C
(which, by the IH, is (n – 2) · 180°). Therefore, the sum of the angles
in A is (n–1) · 180°. Thus P(n + 1) holds, completing the induction. ■
A Different Proof Approach
Using Induction
●
●
Many proofs that work by induction can
be written non-inductively by using
similar arguments.
Don't feel that you have to use induction;
it's one of many tools in your proof
toolbox!
Variations on Induction: Bigger Steps
Subdividing a Square
For what values of n can a square be
subdivided into n squares?
The Key Insight
The Key Insight
●
●
If we can subdivide a square into n squares, we
can also subdivide it into n + 3 squares.
Since we can subdivide a bigger square into 6, 7,
and 8 squares, we can subdivide a square into n
squares for any n ≥ 6:
●
●
●
For multiples of three, start with 6 and keep adding
three squares until n is reached.
For numbers congruent to one modulo three, start
with 7 and keep adding three squares until n is
reached.
For numbers congruent to two modulo three, start
with 8 and keep adding three squares until n is
reached.
Theorem: For any n ≥ 6, it is possible to subdivide a square into n
squares.
Proof: By induction. Let P(n) be “a square can be subdivided into
n squares.” We will prove P(n) holds for all n ≥ 6.
As our base cases, we prove P(6), P(7), and P(8), that a square
can be subdivided into 6, 7, and 8 squares. This is shown here:
2
1
6
3
5
4
1
2
6 7
5 4
3
2
1
3
4
8 7 6 5
For the inductive step, assume that for some n ≥ 6 that P(n) is
true and a square can be subdivided into n squares. We prove
P(n + 3), that a square can be subdivided into n + 3 squares.
To see this, obtain a subdivision of a square into n squares.
Then, choose a square and split it into four equal squares.
This removes one of the n squares and adds four more, so
there are now n + 3 total squares. Thus P(n + 3) holds,
completing the induction. ■
Generalizing Induction
●
When doing a proof by induction:
●
●
●
Feel free to use multiple base cases.
Feel free to take steps of sizes other than
one.
Just be careful to make sure you cover all
the numbers you think that you're
covering!
Variations on Induction: Complete Induction
An Observation
P(n) → P(n + 1)
P(0)
P(1)
P(2)
P(3)
P(4)
P(5)
An Observation
●
In a proof by induction, the inductive
step works as follows:
●
●
●
●
Assume that for some particular n that P(n)
is true.
Prove that P(n + 1) is true.
Notice: When trying to prove P(n + 1),
we already know P(0), P(1), P(2), …, P(n)
but only assume P(n) is true.
Why are we discarding all the
intermediary results?
Complete Induction
●
If the following are true:
●
●
●
●
P(0) is true, and
If P(0), P(1), P(2), …, P(n) are true, then P(n+1)
is true as well.
Then P(n) is true for all n ∈ ℕ.
This is called the principle of complete
induction or the principle of strong
induction.
●
(A note: this also works starting from a number
other than 0; just modify what you're assuming
appropriately.)
Proof by Complete Induction
●
State that your proof works by complete induction.
●
State your choice of P(n).
●
●
Prove the base case: state what P(0) is, then prove it
using any technique you'd like.
Prove the inductive step:
●
●
●
State that for some arbitrary n ∈ ℕ that you're
assuming P(0), P(1), …, P(n) (that is, P(n') for all
natural numbers 0 ≤ n' ≤ n.)
State that you are trying to prove P(n + 1) and what
P(n + 1) means.
Prove P(n + 1) using any technique you'd like.
Example: Polygon Triangulation
Polygon Triangulation
●
Given a convex polygon, an elementary
triangulation of that polygon is a way of
connecting the vertices with lines such
that
●
●
●
No two lines intersect, and
The polygon is converted into a set of
triangles.
Question: How many lines do you have to
draw to elementarily triangulate a
convex polygon?
Elementary Triangulations
Elementary Triangulations
Elementary Triangulations
Some Observations
●
●
●
Every elementary triangulation of the same
convex polygon seems to require the same
number of lines.
The number of lines depends on the number
of vertices:
●
5 vertices: 2 lines
●
6 vertices: 3 lines
●
8 vertices: 5 lines
Conjecture: Every elementary triangulation
of an n-vertex convex polygon requires n – 3
lines.
Elementary Triangulations
n–k+2
vertices
k
vertices
Theorem: Every elementary triangulation of a convex polygon with n
vertices requires n – 3 lines.
Proof: By complete induction. Let P(n) be “every elementary
triangulation of a convex polygon requires n–3 lines.” We prove
P(n) holds for all n ≥ 3. As a base case, we prove P(3):
elementarily triangulating a convex polygon with three vertices
requires no lines. Any polygons with three vertices is a triangle,
so any elementary triangulation of it will have no lines.
For the inductive step, assume for some n ≥ 3 that P(3), P(4), …,
P(n) are true. This means any elementary triangulation of an
n'-vertex convex polygon, where 3 ≤ n' ≤ n, uses n'–3 lines. We
prove P(n+1): any elementary triangulation of any (n+1)-vertex
convex polygon uses n–2 lines.
Let A be an arbitrary convex polygon with n+1 vertices. Pick any
elementary triangulation of A and select an arbitrary line in that
triangulation. This line splits A into two smaller convex polygons
B and C, which are also triangulated. Let k be the number of
vertices in B, meaning C has (n+1)–k+2 = n–k+3 vertices. By our
inductive hypothesis, any triangulations of B and C must use k–3
and n–k lines, respectively. Therefore, the total number of lines in
the triangulation of A is n–k+k–3+1 = n–2. Thus P(n+1) holds,
completing the induction. ■
Using Complete Induction
●
●
When is it appropriate to use complete
induction in contrast to standard induction?
Depends on the proof approach:
●
●
●
Typically, standard induction is used when a
problem of size n + 1 is reduced to a simpler
problem of size n.
Typically, complete induction is used when the
problem of size n + 1 is split into multiple
subproblems of unknown but smaller sizes.
It is never “wrong” to use complete induction.
It just might be unnecessary. We suggest
writing drafts of your proofs just in case.
Summary
●
●
●
●
Induction doesn't have to start at 0. It's
perfectly fine to start induction later on.
Induction doesn't have to take steps of size 1.
It's not uncommon to see other step sizes.
Induction doesn't have to have a single base
case.
Complete induction lets you assume all prior
results, not just the last result.
Next Time
●
Graphs
●
Representing relationships between objects.
●
Connectivity in graphs.
●
Planar graphs.