Download PRACTICE: Mixed practice with roots √4 = √144 = √9 = √64

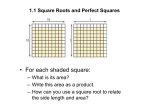
PRACTICE: Mixed practice with roots
LEVEL 1
1) REVIEW: What are the 1st 12 perfect squares?
2) REVIEW: What are the 1st 6 perfect cubes?
3) How would you describe the relationship between squaring and finding the
square root?
4) Why is the square root of a negative number undefined within the world of real
numbers?
5) Do as much as you can here without a calculator. Then use the calculator for
the rest. Write “undefined” where appropriate (for the world of real numbers).
√4 =
√1 =
√36 =
√169 =
√
9
16
=
3
√8 =
3
√216 =
3
√– 125 =
√144 =
√– 100 =
√121 =
√225 =
4
√9 =
√81 =
√0 =
√900 =
√ =
9
√
3
3
√1 =
3
√512 =
3
√
27
64
=
25
81
√64 =
√49 =
√– 25 =
√400 =
√
=
√64 =
3
√0 =
3
1
3
3
√
216
=
121
144
√
=
√27 =
3
√343 =
1
√
0
√25 =
√16 =
√100 =
√256 =
100
=
3
√125 =
3
√1000 =
3
√
=
0
–729
1331
=
6) REVIEW:
(–5)2 =
71 =
–52 =
01 =
(–4)3 =
3 2
(– )
4
=
–43 =
3 2
–( )
4
=
D. Stark 1/2/2017
1
LEVEL 2
7) Use your calculator to simplify the given non-perfect roots & then find their
decimal approximations to the nearest 100th. Not all roots can be simplified.
exact root
decimal approximation
(rounded to the nearest hundredth.)
𝒆𝒙𝒂𝒎𝒑𝒍𝒆 √𝟕𝟐
8.49
𝟔√𝟐
√192
√300
√101
8) Determine what two whole numbers the given non-perfect roots lie between.
(Use your knowledge of perfect squares to help you.) Then use your calculator
to find the decimal approximation rounded to the nearest tenth.
EXAMPLE: √12 Since √9 = 3 and √16 = 4 and since 12 is between 9 & 16,
then √12 must be between 3 and 4. The calculator says  3.5
between… and…
decimal approximation
(rounded to the nearest tenth)
𝐄𝐗𝐀𝐌𝐏𝐋𝐄 √𝟏𝟐
𝟑
4
3.5
√28
√50
LEVEL 3
9) Simplify the given non-perfect roots without the calculator.
You’ll need to find a perfect square factor of the given number.
EXAMPLES: √12 = √4  3 = √4  √3 = 2  √3 = 2√3
√50 = √25  2 = √25  √2 = 5  √2 = 5√2
exact root
𝒆𝒙𝒂𝒎𝒑𝒍𝒆 √𝟏𝟐
𝟐√𝟑
√18
√75
D. Stark 1/2/2017
2
PRACTICE: Mixed practice with roots
KEY
1) REVIEW: What are the 1st 12 perfect squares?
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144
2) REVIEW: What are the 1st 6 perfect cubes? 1, 8, 27, 64, 125, 216
3) How would you describe the relationship between squaring and finding the
square root?
Just like multiplying and dividing, squaring and finding the square root are
opposites. Finding the square root is like squaring “backwards.”
3 squared is 9 so the positive square root of 9 is 3.
4) Why is the square root of a negative number undefined within the world of real
numbers?
To find the square root of a number, you ask yourself: what times itself
gives me that number? But when you multiply 2 positives, you get a
positive; and when you multiply 2 negatives, you again get a positive.
Within the world of real numbers, there’s no way to multiply just 2 of the
same thing and get a negative. (Once you get to imaginary numbers, there
is a way, but that’s later in your math career.  )
D. Stark 1/2/2017
3
5)
√4 = 2
√1 = 1
√144 = 12 √9 = 3
√– 100 = √81 = 9
√64 = 8
√49 = 7
√25 = 5
√16 = 4
√– 25 =
√100 = 10
undefined
√36 = 6
√121 = 11 √0 = 0
undefined
√169 = 13 √225 = 15 √900 = 30 √400 = 20 √256 = 16
√
9
16
=
𝟑
𝟒
4
𝟐
√ =
9 𝟑
√
3
3
25
81
=
𝟓
√
𝟗
121
144
=
𝟏𝟏
√
𝟏𝟐
100
=
0
undefined
3
√8 = 2
3
√216 = 6
3
√– 125 =
–5
√1 = 1
3
√512 = 8
3
√
27
64
=
𝟑
𝟒
√64 = 4
3
√0 = 0
3
𝟏
3
3
√
1
216
=
3
√27 = 3
3
√343 = 7
1
√
𝟔
0
√125 = 5
3
√1000 = 10
3
√
=
–729
1331
=–
𝟗
𝟏𝟏
undefined
6) REVIEW:
(–5)2 = 25
71 = 7
–52 = –25
01 = 0
(–4)3 = –64 –43 = –64
3 2
(– )
4
=
𝟗
𝟏𝟔
3 2
–( )
4
=–
𝟗
𝟏𝟔
D. Stark 1/2/2017
4
7)
exact root
decimal approximation
(rounded to the nearest hundredth.)
𝒆𝒙𝒂𝒎𝒑𝒍𝒆 √𝟕𝟐
√192
√300
√101
8.49
13.86
17.32
10.05
𝟔√𝟐
𝟖√𝟑
𝟏𝟎√𝟑
√𝟏𝟎𝟏
8)
between…
and…
decimal
approximation
(rounded to the
nearest tenth.)
𝐄𝐗𝐀𝐌𝐏𝐋𝐄 √𝟏𝟐
√28
√50
𝟑
𝟓
𝟕
4
𝟔
𝟖
3.5
5.3
7.1
9)
exact root
𝒆𝒙𝒂𝒎𝒑𝒍𝒆 √𝟏𝟐
√18
√75
𝟐√𝟑
𝟑√𝟐
𝟓√𝟑
D. Stark 1/2/2017
5