Download Relativity 1 - UCF College of Sciences

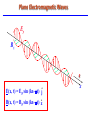
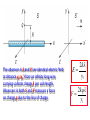
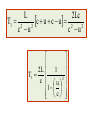
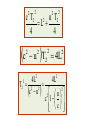
Relativity
Chapter 1
Modern physics is the study of the two great
revolutions in physics - relativity and quantum
mechanics.
Galilean Relativity
All inertial reference frames are equivalent! Another way of stating
this principle is that only relative motion can be detected.
Transformation Equations
If you know what an observer in a particular reference frame
observes then you can
predict the observations made by an
observer in any other reference frame. The
equations that
enable you to make these calculations are called Transformation
Equations.
Invariance
Since the labeling of your coordinate axis and its origin location
is arbitrary, the
equations of physics should have the same
form regardless when you rotate or translate your axis set.
Equations that have this property are said to be invariant to the
transformation.
It was shown that Maxwell's Equations are not
invariant under a Galilean Transformation so E&M and
Mechanics are not consistent.
IV. Important Physics Problems of Late 19th
Century
Modern Physics was developed as the solution to some
extremely important problems in the late 19th century that
stumped physicists. We will study these important
problems and see how they have caused us to change our
notions of time, space, and matter. Some of these
important problems include
a) the ether problem,
b) stability of the atom,
c) blackbody radiation,
d) photoelectric effect, and
e) atomic spectra.
A Brief Overview of Modern Physics
20th Century revolution:
- 1900 Max Planck
Basic ideas leading to Quantum theory
- 1905 Einstein
Special Theory of Relativity
21st Century
Story is still incomplete
Basic Problems
 Newtonian mechanics fails to describe properly
the motion of objects whose speeds approach
that of light
 Newtonian mechanics is a limited theory
– It places no upper limit on speed
– It is contrary to modern experimental results
– Newtonian mechanics becomes a specialized case of
Einstein’s special theory of relativity when speeds are
much less than the speed of light
Galilean Relativity
 To describe a physical event, a frame of
reference must be established
 There is no absolute inertial frame of
reference
– This means that the results of an experiment
performed in a vehicle moving with uniform
velocity will be identical to the results of the same
experiment performed in a stationary vehicle
Galilean Relativity
 Reminders about inertial frames
– Objects subjected to no forces will experience no acceleration
– Any system moving at constant velocity with respect to an
inertial frame must also be in an inertial frame
 According to the principle of Galilean relativity, the
laws of mechanics are the same in all inertial frames of
reference
Galilean Relativity
 The observer in the
truck throws a ball
straight up
– It appears to move in a
vertical path
– The law of gravity and
equations of motion
under uniform
acceleration are
obeyed
Galilean Relativity
 There is a stationary observer on the ground
– Views the path of the ball thrown to be a parabola
– The ball has a velocity to the right equal to the velocity of
the truck
Galilean Relativity – conclusion
 The two observers disagree on the shape of the ball’s
path
 Both agree that the motion obeys the law of gravity
and Newton’s laws of motion
 Both agree on how long the ball was in the air
Conclusion: There is no preferred frame of reference
for describing the laws of mechanics
Frames of Reference and Newton's Laws
The cornerstone of the theory of special relativity is the
Principle of Relativity:
The Laws of Physics are the same in all inertial frames of
reference.
We shall see that many surprising consequences follow from this
innocuous looking statement.
Let us review Newton's mechanics in terms of frames of reference.
A point in space is specified by
its three coordinates (x,y,z)
and an "event" like, say, a little
explosion by a place and time
– (x,y,z,t).
A "frame of reference" is just a set of coordinates - something you
use to measure the things that matter in Newtonian mechanical
problems - like positions and velocities, so we also need a clock.
The "laws of physics" we shall consider are those of Newtonian
mechanics, as expressed by Newton's laws of motion, with
gravitational forces and also contact forces from objects pushing
against each other.
_____________________________
For example, knowing the universal gravitational
constant from experiment (and the masses involved),
it is possible from Newton's second law,
force = mass x acceleration,
to predict future planetary motions with great
accuracy.
Suppose we know from experiment that these laws
of mechanics are true in one frame of reference. How
do they look in another frame, moving with respect to
the first frame? To figure out, we have to find how to
get from position, velocity and acceleration in one
frame to the corresponding quantities in the second
frame.
Obviously, the two frames must have a constant
relative velocity, otherwise the law of inertia won't
hold in both of them.
Let's choose the coordinates so that this velocity is along the xaxis of both of them.
Notice we also throw in a clock with each frame.
Now what are the coordinates of the event (x,y,z,t) in S'?
It's easy to see t' = t - we synchronized the clocks when O‘
passed O. Also, evidently, y' = y and z' = z, from the figure.
We can also see that x = x' +vt. Thus (x,y,z,t) in S
corresponds to (x',y',z', t' ) in S', where
x  x  vt
y  y
z  z
t  t
That's how positions transform - these are known as the Galilean
transformations.
What about velocities ? The velocity in S' in the x' direction
dx dx d
dx
ux 

 ( x  vt) 
 v  ux  v
dt  dt dt
dt
This is just the addition of velocities formula
u x  ux  v
How does acceleration transform?
dux dux d
du x

 (u x  v) 
dt 
dt
dt
dt
Since v is constant we have
ax  ax
the acceleration is the same in both frames. This again is
obvious - the acceleration is the rate of change of
velocity, and the velocities of the same particle
measured in the two frames differ by a constant factor the relative velocity of the two frames.
If we now look at the motion under gravitational forces, for
example,
 Gm1m2
ˆ
m1a 
r
2
r
we get the same law on going to another inertial frame because
every term in the above equation stays the same.
Note that acceleration is the rate of change of momentum this is the same in both frames. So, in a collision, if total
momentum is conserved in one frame (the sum of individual
rates of change of momentum is zero) the same is true in all
inertial frames.
Maxwell’s Equations of Electromagnetism
in Vacuum
Gauss’ Law for Electrostatics

The total electric flux through any closed surface equals the
net charge inside that surface divided by ε0
Gauss’ Law for Magnetism

The net magnetic flux through a closed
surface is zero
Faraday’s Law of Induction
The line integral of the electric field around any
closed path (the emf), equals the rate of change
of magnetic flux through surface area bounded
by that path
Ampere’s Law
The line integral of the magnetic field around any
closed path is the sum of μ0 times the net current
through that path and ε0μ0 times the rate of change of
electric flux through any surface bounded
by that path
E  dA 


q
0
B  dA  0
d B
E  d  
dt
d E
B  d   0 I  0 0
dt
The Equations of Electromagnetism
Faraday’s Law
3

d B
E  d  
dt
Ampere’s Law
4

d E
B  d   0 0
dt
.. if you change a
magnetic field you
induce an electric
field.........
.. if you change an
electric field you
induce a magnetic
field.........
Electromagnetic Waves
Faraday’s law:
dB/dt
electric field
Maxwell’s modification of Ampere’s law
dE/dt
magnetic field
d E
 B  dl  00 dt
d B
 E  dl   dt
These two equations can be solved simultaneously.
The result is:
E(x, t) = EP sin (kx-t) ĵ
B(x, t) = BP sin (kx-t) ẑ
Plane Electromagnetic Waves
Ey
Bz
c
E(x, t) = EP sin (kx-t) ĵ
B(x, t) = BP sin (kx-t) ẑ
x
Plane Electromagnetic Waves
Ey
E(x, t) = EP sin (kx-t) ĵ
B(x, t) = BP sin (kx-t) ẑ
Bz
Notes: Waves are in Phase,
but fields oriented at 900.
k=2π/λ.
Speed of wave is c=ω/k (= fλ)
c  1/  00  3  10 m / s
8
c
x
At all times
E=cB
It was recognized that the Maxwell equations did not
obey the principles of Newtonian relativity. i.e. the
equations were not invariant when transformed between
the inertial reference frames using the Galilean
transformation.
Lets consider an example of infinitely long wire
with a uniform negative charge density λ per
unit length and a point charge q located a
distance y1 above the wire.
S’
The observer in S and see identical electric field
at distance y1=y1’ from an infinity long wire
carrying uniform charge λ per unit length.
Observers in both S and S’ measure a force
on charge q due to the line of charge.
2k
E
y1
2kq
F
y1
 0 v 2 q
2y1
However, the S’ observer measured and additional force
due to the magnetic field at y1’ arising from the motion
of the wire in the -x’ direction. Thus, the electromagnetic force does
not have the same form in different inertial systems, implying that
Maxwell’s equations are not invariant under a Galilean
transformation.
Speed of the Light
It was postulated in the nineteenth century that
electromagnetic waves, like other waves, propagated in
a suitable material media, called the ether.
In according with this postulate the ether filed the
entire universe including the interior of the matter.
It had the inconsistent properties of being
extremely rigid (in order to support the stress of the
high electromagnetic wave speed), while offering no
observable resistance to motion of the planet, which
was fully accounted for by Newton’s law of gravitation.
Speed of the Light
The implication of this postulate is that a light
wave, moving with velocity c with respect to the
ether, would travel at velocity c’=c +v with respect
to a frame of reference moving through the ether at
v.
This would require that Maxwell’s equations
have a different form in the moving frame so as to
predict the speed of light to be c’, instead of
c
1
0 0
Conflict Between Mechanics and E&M
A. Mechanics
Galilean relativity states that it is impossible for
an observer to experimentally distinguish
between uniform motion in a straight line and
absolute rest. Thus, all states of uniform
motion are equal.
Conflict Between Mechanics and E&M
B. E&M
InitiallyThe initial interpretation of the speed of light in
Maxwell's theory was this c was the speed of light
seen by observers in absolute rest with respect to
the ether.
In other reference frames, the speed of light
would be different from c and could be obtained by
the Galilean transformation.
ProblemIt would now be possible for an observer
to distinguish between different states of
uniform motion by measuring the speed of
light or doing other electricity, magnetism,
and optics experiments.
Possible Solutions
1. Maxwell's theory of electricity and magnetism
was flawed. It was approximately 20 years old while
Newton's mechanics was approximately 200 years old.
2. Galilean relativity was incorrect. You can detect
absolute motion!
3. Something else was wrong with mechanics (I.e
Galilean transformation).
Experimental Results
Most physicists felt that Maxwell's equations were
probably in error.
Numerous experiments were performed to detect
the motion of the earth through the ether wind.
The most famous of these experiments was the
Michelson-Morley experiment. Because of the
tremendous precision of their interferometer, it was
impossible for Michelson and Morley to miss detecting
the effect of the earth's motion through the ether
unless mechanics was flawed!
The Michelson-Morley experiment is a race between light beams. The
incoming light beam is split into two beams by a half-silvered mirror. The
beams follow perpendicular paths reflecting off full mirrors before
recombining back at the half mirror. Time differences are seen in the
interference pattern on the screen.
Theory
We will simplify the calculations by assuming
that L1 = L2 = L.
The time required to complete path 1
(horizontal path) is given by
L
L
T1 

cu cu
where we have used the Galilean transformation
and velocity = distance/time.
L
2Lc


T1  2
c

u

c

u

2
2
2
c u
c u




2L 
1

T1 
2 

c
u
1    
  c  
V. Binomial Approximation
The Binomial Expansion is a powerful method for approximating
small effects in physics and engineering problems. It is
extremely useful in both special
relativity and
electromagnetism problems even when you have a calculator.
The expansion of the nth power of (1+x) is given by
n n -1 2
n
1 x  1 n x 
x  ...
2
The Binomial approximation states that when x << 1
1 x n  1 n x
Since u<<c, we can use the binomial
approximation:
2L   u 
T1 
1   
c   c 
2



We can determine the time required to complete path
2 (vertical path) using the distance diagram below:
u(T2/2)
u(T2/2)
Using the Pythagorean theorem, we have:
2
 T2 
 T2 
2
c
 L  u



2
2




2
2
2
2
c T2
2 u T2
L 
4
4
c
2

2
 u T2  4L
2
2
2
2
2
4L
4L
T2  2 2 
2
c u
 u 
2
c 1    
  c  
2


T2 
2L
u
c 1  
c
2
Again, using the binomial approximation:
2

2L
1u 
T2 
1    
c  2  c  
Thus, the time difference for the two paths is
approximately
2
2


L 1u
Lu
ΔT  T1 - T2  2       
c  2  c   c  c 
We can now calculate the phase shift in terms of
wavelengths as follows:
f λc
λ
c
T
λ  cT
Thus, the phase shift in terms of a fraction of a
wavelength is given by
u
 λ  c T  L  
c
λ Lu
  
λ
λ c
2
2
Using a sodium light,  = 590 nm, and a
interferometer with L = 11 m, we have
 4
Δλ 
11 m

 
10
7

λ
 5.90 x 10 m 


2
 0.2
This was a very large shift (20%) and couldn't
have been overlooked.
Result - No shift was ever observed regardless
of when the experiment was performed or
how the interferometer was orientated!