Download I1 Pythagoras` Theorem and Introduction Trigonometric Ratios

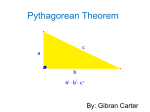
Mathematics SKE: STRAND I
UNIT I1 Pythagoras' Theorem and Trigonometric Ratios: Introduction
I1 Pythagoras' Theorem and
Trigonometric Ratios
Introduction
Learning objectives
This is the first of five units on Trigonometry and related topics; Pythagoras' Theorem is an important
topic with many applications in design, architecture, surveying, navigation, etc. After completing Unit
I1 you should
•
understand and be able to use Pythagoras' Theorem in right angled triangles
•
be able to apply Pythagoras' Theorem when finding the length of an unknown side in a right
angled triangle
•
understand how to calculate the trigonometric functions, sine, cosine and tangent, in a right
angled triangle
•
be able to find the length of a side in a right angled triangle, given one side and one angle.
Introduction
Very little is known of the life of Pythagoras, but he was born on the island of Samos and is credited
with the founding of a community at Crotona in Southern Italy by about 530 BC. The community had
religious and political purposes, but also dealt with mathematics, especially the properties of whole
numbers or positive integers.
Mystical attributes, such as that odd numbers were male and
even numbers female, were ascribed to numbers. In addition
descriptions of arithmetical properties of integers were found.
The 4th triangle number or
'Holy tetractys' had mystical
significance for the
Pythagoreans
The diagram on the right shows that
1 = 12
1 + 3 = 22
1 + 3 + 5 = 32
The sum of consecutive odd
numbers, starting at 1, is a
square number
The Pythagoreans also formulated the idea of proportions in
relation to harmonics on stringed instruments. The theorem with
which Pythagoras' name is associated was probably only proved
later. Specific instances of it were certainly known to the
Babylonians. The 'Harpedonaptai', Egyptian rope stretchers, are
said to have used the 3, 4, 5 triangle to obtain right angles from
equally spaced knots on cords. The ancient Chinese also knew that
the 3, 4, 5 triangle was right angled.
© CIMT, Plymouth University
1
a2
b
2
b
a
c
c2
Pythagoras' Theorem:
a2 + b2 = c2
Mathematics SKE: STRAND I
UNIT I1 Pythagoras' Theorem and Trigonometric Ratios: Introduction
I1 Pythagoras' Theorem and
Trigonometric Ratios
Introduction
The Greeks used 'chord' tables rather than tables of trigonometric functions, and the development of
trigonometric tables took place around 500 AD, through the work of Hindu mathematicians. In fact,
tables of sines for angles up to 90° were given for 24 equal intervals of 3 43 ° each. The value of 10
was used for π at that time. Further work a century later, particularly by the Indian mathematician
Brahmagupta (in 628), led to the sine rule as we know it today.
A useful course book for the historical introduction of these topics is 'Ascent of Man' by
Jacob Bronowski, published in 1974.
Key points and principles
•
Pythagoras' Theorem states that:
In any right angled triangle, the area of the square on
the hypotenuse (the side opposite the right angle) is
equal to the sum of the areas of the squares on the
other two sides (the two sides that meet at the right
angle).
c
a
Note that a right angle is indicated by a small 'box'
at an angle which is 90° .
b
•
In a right angled triangle, you can use Pythagoras
Theorem,
c2 = a2 + b2
to find the length of c, the hypotenuse,
and
a2 = c2 − b2
(or b 2 = c 2 − a 2 )
to find the length of a (or b), given the lengths of b and c (or c and a).
•
In a right angled triangle, the side opposite the
marked angle is the opposite (opp), a in the diagram;
the hypotenuse (hyp) is the longest side, c, and the
other side is the adjacent side (adj), b in the diagram.
c
a
θ
b
© CIMT, Plymouth University
2
UNIT I1 Pythagoras' Theorem and Trigonometric Ratios: Introduction
Mathematics SKE: STRAND I
I1 Pythagoras' Theorem and
Trigonometric Ratios
•
Introduction
In a right angled triangle, given an angle θ and the
length of one side, you can use
sin θ
=
opp
hyp
=
a
c
cos θ
=
adj
hyp
=
b
c
tan θ
=
opp
adj
=
a
b
or
to find the lengths of the other two sides and to find angles, using the SHIFT button on a
calculator
(opp : opposite; hyp : hypotenuse; adj : adjacent)
[Note that calculators should be in degree mode for trigonometric calculations.]
For example,
(ii)
(i)
given c,
given a,
c =
a = c sin θ ,
b = c cos θ
a
,
sin θ
a
,
tan θ
b =
etc.
Facts to remember
•
a 2 + b 2 = c 2 in a right angled triangle (Pythagoras' Theorem)
c
a
•
in the right angled triangle shown,
© CIMT, Plymouth University
opp
a
sin θ =
=
hyp
c
cos θ =
adj
b
=
hyp
c
tan θ =
opp
a
=
adj
b
3
θ
b
Mathematics SKE: STRAND I
UNIT I1 Pythagoras' Theorem and Trigonometric Ratios: Introduction
I1 Pythagoras' Theorem and
Trigonometric Ratios
Introduction
Glossary of terms
• opposite (opp), adjacent (adj) and hypotenuse (hyp) in
right angled triangles defined for angle θ , as in the diagram
hyp
opp
Remember: the hypotenuse is always the side opposite
the right angle, and is the longest side
θ
adj
•
sin θ =
a
c
⎛ opp ⎞
⎜=
⎟
⎝ hyp ⎠
cos θ =
b
c
⎛ adj ⎞
⎜=
⎟
⎝ hyp ⎠
a
tan θ =
b
⎛ opp ⎞
⎜=
⎟
⎝ adj ⎠
c
a
θ
b
in right angled triangles
© CIMT, Plymouth University
4