Download Review Sheet for Test 3

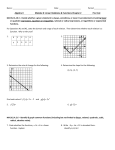
Math 101-08
11–13–2008
Review Sheet for Test 3
These problems are provided to help you study. The presence of a problem on this handout does not
imply that there will be a similar problem on the test. And the absence of a topic does not imply that it
won’t appear on the test.
1. (a) Find the slope of the line passing through (1, 3) and (−2, −5).
(b) Find the slope and y-intercept of the line 3x − 6y = 18.
(c) Find the x and y-intercepts of the line 7x − 2y = 21. Then use them to graph the line.
2. (a) Find the equation of the line which passes through the point (2, −3) and is parallel to the line
y = −17x + 21. Write your answer in slope-intercept form.
(b) Find the equation of the line which is perpendicular to the line 8x − 2y = 5 and which has y-intercept
13.
3. (a) Find the equation of the line with slope 7 which passes through the point (1, −5).
(b) Find the equation of the line which passes through the points (1, −3) and (2, 5).
(c) Find the equation of the line with slope 5 and y-intercept 42.
(d) What is the x-intercept of the line y = 7x − 28?
(e) Find the equation of the line which is parallel to 2x + 7y + 8 = 0 and passes through the point (4, −9).
(f) Find the slope of a line which is perpendicular to the line containing the points (2, 3) and (0, −8).
(g) Find the equation of the vertical line which passes through the point (17, −33).
(h) Find the equation of the line whose graph is shown below.
y
1
x
-3
(i) Graph the line −3x + 2y = 6 by finding the x-intercept and y-intercept.
(j) What is the x-intercept of the line y = 11?
(k) Find the point or points of intersection of the lines
3x + 2y = 4 and
2x + y = −7.
4. Solve the system of equations
5x + 2y = 8
2x + y = 1
1
5. Solve the system of equations
3x − 2y = 7
−9x + 6y = 10
6. Solve the system of equations
2x + 5y = 7
0.4x + y = 1.4
7. Solve the following system:
2x + 3y = 11
3x − 2y = −16
8. Solve the following system:
2x − 3y = 11
−4x + 6y = −25
9. (a) Express 163/4 as an integer or a fraction.
(b) Express (−125)−2/3 as an integer or a fraction.
√
(c) Simplify 125.
√
(d) Simplify 3 54.
√
√
(e) Simplify 7 72 − 3 50.
√
3− 5
√ .
10. (a) Rationalize
2+ 5
√
1+2 3
√ .
(b) Rationalize
5− 3
11. (a) Simplify (2x3/10 )2 (y −1/4 )3 (x1/5 y 1/6 )3 , writing your answer using positive exponents.
p
(b) Simplify 16x2 y 6 , without making any assumptions about the signs of the variables.
(x1/2 y 1/3 )2
(2x1/4 )6
, writing your answer using positive exponents.
(c) Simplify
(y 1/6 )2
4(x−3/4 )−2
p
(d) Simplify 3 250x10 y 8 .
s
2x6 y 10 z
.
(e) Simplify 3
16x5 y
12. (a) Multiply out: (2x1/2 + x1/3 )(x1/2 − 5x1/3 ).
√
(b) Multiply out: ( 2x + 5 − 7)2 .
√
√
(c) Multiply out: ( x + 1 + x + 4)2 .
13. Simplify the following complex numbers, writing each result in the form a + bi:
(a) i43 .
(b) (4 + 5i)(3 − 2i).
2
(c)
1
.
3 + 4i
(d) 3i +
2i
.
4 + 5i
(e)
3 − 2i
.
5 + 7i
(f)
3
i
−
.
4 + i 3 + 2i
14. What is wrong with the following computation?
“ − 1 = i2 =
√
−1 ·
p
√
√
−1 = (−1) · (−1) = 1 = 1”
15. The area of a rectangle is 84 square miles. The length is 4 miles less than 3 times the width. Find the
dimensions.
16. The length of a rectangle is 2 less than 3 times the width. The area is 176. Find the dimensions of the
rectangle.
17. The sum of two numbers is 5. The sum of their reciprocals is
45
. Find the two numbers.
44
18. Calvin and Bonzo, eating together, can eat 540 rib sandwiches in 6 hours. Eating alone, Calvin can eat
240 rib sandwiches in 4 hours less than it takes Bonzo, eating alone, to eat 240 rib sandwiches. How long
does it take Calvin, eating alone, to eat 240 rib sandwiches?
19. Solve the following quadratic equations:
(a) (x − 4)2 = 25.
(b) (2x − 3)2 = −16.
(c) x2 + 4x + 1 = 0.
(d) x2 − 6x + 25 = 0.
(e) 10x2 + 18 = 27x.
(f) x2 − 4x + 29 = 0.
(g) x2 + 2x = −10.
20. Solve for x:
√
(a) x − 3 = x + 3.
√
√
(b) x + 12 − x = 2.
√
(c) x + 2 = 7x + 2.
√
√
√
(d) x + 3 + x + 11 = 2x + 20.
21. Solve the following equations for x. (Complex number solutions are allowed.)
(a) x10 − x5 − 2 = 0.
(b) (x − 5)2 − 7(x − 5) − 8 = 0.
(c) x4 − 5x2 − 14 = 0.
3
22. (a) Show that no matter what k is, the following equation has complex roots:
x2 − 4x + (k2 + 5) = 0.
(b) For what value or values of p does the equation 2x2 − px + 50 = 0 have exactly one root?
23. Find the distance from (3, −4) to (7, 1).
24. Find the center and radius of the circle
x2 + 6x + y 2 − 14y = 6.
25. Find the center and radius of the circle
x2 + 3x + y 2 − 4y = 6.
Solutions to the Review Sheet for Test 3
1. (a) Find the slope of the line passing through (1, 3) and (−2, −5).
m=
3 − (−5)
8
= .
1 − (−2)
3
(b) Find the slope and y-intercept of the line 3x − 6y = 18.
Put the equation into slope-intercept form by solving for y:
3x −
− 3x
/
6y
−6y
−6
y
The slope is
=
18
3x
= −3x +
−6
1
=
x −
2
18
−6
3
1
and the y-intercept is −3.
2
(c) Find the x and y-intercepts of the line 7x − 2y = 21. Then use them to graph the line.
21
21
Setting x = 0, I get −2y = 21, so y = − . The y-intercept is − .
2
2
Setting y = 0, I get 7x = 21, so x = 3. The x-intercept is 3.
2.5
-1
1
2
-2.5
-5
-7.5
-10
-12.5
4
3
4
2. (a) Find the equation of the line which passes through the point (2, −3) and is parallel to the line
y = −17x + 21. Write your answer in slope-intercept form.
The line y = −17x + 21 has slope −17. The line I want is parallel to this line, so it also has slope −17.
It passes through the point (2, −3), so the point-slope form is
y + 3 = −17(x − 2).
Multiply out the right side, then solve for y:
y
y
−
y
+ 3 =
−17(x − 2)
+ 3 = −17x
+
34
3
3
= −17x
+
31
(b) Find the equation of the line which is perpendicular to the line 8x − 2y = 5 and which has y-intercept
13.
Solve 8x − 2y = 5 for y to find the slope:
8x −
− 8x
/
2y
=
5
8x
= −8x +
−2
−2y
−2
y
=
4x
−
5
−2
5
2
1
The given line has slope 4. The line I want is perpendicular to the given line, so it has slope − . Since
4
the line I want has y-intercept 13, its equation is
1
y = − x + 13.
4
3. (a) Find the equation of the line with slope 7 which passes through the point (1, −5).
7(x − 1) = y + 5.
(b) Find the equation of the line which passes through the points (1, −3) and (2, 5).
The slope is m =
5 − (−3)
= 8, so the line is
2−1
8(x − 1) = y + 3.
(c) Find the equation of the line with slope 5 and y-intercept 42.
y = 5x + 42.
(d) What is the x-intercept of the line y = 7x − 28?
Set y = 0:
0 = y = 7x − 28,
7x = 28,
x = 4.
(e) Find the equation of the line which is parallel to 2x + 7y + 8 = 0 and passes through the point (4, −9).
5
First, put the given line into slope-intercept form:
2x
−
÷
+ 7y
7y
+
0
7y
+ 8 = −7y
−7
−7
8
−
=
y
7
2x
−7
2
− x
7
8
=
2
The given line has slope − .
7
2
Since the line I want is parallel to the given line, the line I want also has slope − .
7
The line I want passes through the point (4, −9).
Therefore, the line is
2
y + 9 = − (x − 4).
7
(f) Find the slope of a line which is perpendicular to the line containing the points (2, 3) and (0, −8).
The line containing the points (2, 3) and (0, −8) has slope
11
3 − (−8)
=
.
2−0
2
A line perpendicular to this line has slope equal to the negative reciprocal of
11
2
, which is − .
2
11
(g) Find the equation of the vertical line which passes through the point (17, −33).
A vertical line has an equation of the form x = (a number). In this case, the number is the x-coordinate
of (17, −33) — that is, 17. So the vertical line which passes through the point (17, −33) is x = 17.
(h) Find the equation of the line whose graph is shown below.
y
1
x
-3
The y-intercept of the line is b = 1.
1
. (You can also
3
find the slope by picking two points on the line — for example, (−3, 0) and (0, 1) — and applying the slope
formula.)
Therefore, the line is
1
y = x + 1.
3
The line rises 1 unit for every 3 units it moves to the right. Therefore, the slope is
(i) Graph the line −3x + 2y = 6 by finding the x-intercept and y-intercept.
When x = 0, I get 2y = 6, or y = 3.
6
When y = 0, I get −3x = 6, or x = −2.
y
3
x
-2
(j) What is the x-intercept of the line y = 11?
The line y = 11 is a horizontal line 11 units above the x-axis. Therefore, it doesn’t intersect the x-axis,
and there is no x-intercept.
(k) Find the point or points of intersection of the lines
3x + 2y = 4 and
2x + y = −7.
Solve the equations simultaneously. The second equation gives y = −2x − 7, so plugging this into the
first gives
3x + 2(−2x − 7) = 4,
3x − 4x − 14 = 4,
−x − 14 = 4,
−x = 18,
x = −18.
Hence, y = −2(−18) − 7 = 29. The point of intersection is (−18, 29).
4. Solve the system of equations
5x + 2y = 8
2x + y = 1
Multiply the second equation by 2 and subtract it from the first:
5x + 2y
4x + 2y
x
= 8
= 2
= 6
Multiply the first equation by 2, the second equation by 5, and subtract the resulting equations:
10x +
10x +
4y
5y
−y
= 16
= 5
= 11
Multiplying this by −1, I get y = −11. The solution is x = 6 and y = −11.
5. Solve the system of equations
3x − 2y = 7
−9x + 6y = 10
7
Multiply the first equation by 3 and add the second equation:
9x − 6y
−9x + 6y
0
= 21
= 10
= 31
This is a contradiction. Therefore, the system has no solutions.
6. Solve the system of equations
2x + 5y = 7
0.4x + y = 1.4
Multiply the second equation by 5 and subtract it from the first equation:
2x + 5y
2x + 5y
0
= 7
= 7
= 0
This is an identity. Hence, the system has infinitely many solutions.
Note: The answer is not “all real numbers”. There are infinitely many pairs of numbers that solve the
system, but not every pair of numbers is a solution. For example, x = 0 and y = 0 is not a solution.
7. Solve the following system:
2x + 3y = 11
3x − 2y = −16
Multiply the first equation by 2 and the second by 3, then add the resulting equations:
4x +
9x −
13x
x
6y
6y
= 22
= −48
= −26
= −2
Plug x = −2 into 2x + 3y = 11 and solve for y:
−4 + 3y = 11,
3y = 15,
y = 5.
The solution is (−2, 5).
8. Solve the following system:
2x − 3y = 11
−4x + 6y = −25
Multiply the first equation by 2 and add it to the second equation:
4x
−4x
0
− 6y
+ 6y
= 22
= −25
= −3
The last equation is a contradiction. Therefore, there are no solutions.
8
9. (a) Express 163/4 as an integer or a fraction.
√
4
163/4 = ( 16)3 = 23 = 8.
(b) Express (−125)−2/3 as an integer or a fraction.
(−125)−2/3 =
(c) Simplify
(d) Simplify
√
125.
√
3
54.
1
1
1
1
= √
=
.
=
3
2
2
(−5)
25
(−125)2/3
( −125)
√
√
3
125 =
√
√
√
25 5 = 5 5.
√
√
√
3
3
3
54 = ( 27)( 2) = 3 2.
√
√
(e) Simplify 7 72 − 3 50.
√
√ √
√ √
√
√
√
√
√
√
7 72 − 3 50 = 7 36 2 − 3 25 2 = 7 · 6 2 − 3 · 5 2 = 42 2 − 15 2 = 27 2.
√
3− 5
√ .
10. (a) Rationalize
2+ 5
√
√
√
√
√
√
√
√
3− 5 2− 5
(3 − 5)(2 − 5)
6 − 2 5 − 3 5 + ( 5)2
3− 5
√ =
√ ·
√ =
√
√ =
√
=
2+ 5
2+ 5 2− 5
(2 + 5)(2 − 5)
4 − ( 5)2
√
√
√
6−5 5+5
11 − 5 5
=
= −11 + 5 5.
4−5
−1
√
1+2 3
√ .
(b) Rationalize
5− 3
√
√
√
√
√
√
√
1+2 3
1+ 3
1+2 3 5+ 3
5 + 11 3 + 2( 3)2
11 + 11 3
√ =
√ ·
√ =
√
=
.
=
22
2
5− 3
5− 3 5+ 3
25 − ( 3)2
11. (a) Simplify (2x3/10 )2 (y −1/4 )3 (x1/5 y 1/6 )3 , writing your answer using positive exponents.
(2x3/10 )2 (y −1/4 )3 (x1/5 y 1/6 )3 = (22 )(x3/10 )2 (y −1/4 )3 (x1/5 )3 (y 1/6 )3 = 4x3/5 y −3/4 x3/5 y 1/2 =
4x6/5 y −1/4 =
(b) Simplify
4x6/5
.
y 1/4
p
16x2 y 6 , without making any assumptions about the signs of the variables.
√
p
p
√
16x2 y 6 = 16 · x2 · y 6 = 4|x||y|3 .
(x1/2 y 1/3 )2
(2x1/4 )6
(c) Simplify
, writing your answer using positive exponents.
(y 1/6 )2
4(x−3/4 )−2
(x1/2 y 1/3 )2
(x1/2 y 1/3 )2 4(x−3/4 )−2
(x1/2 )2 (y 1/3 )2 4(x−3/4 )−2
xy 2/3 4x3/2
xy 1/3
(2x1/4 )6
=
.
·
=
·
=
·
=
16
(2x1/4 )6
(y 1/6 )2
(26 )(x1/4 )6
(y 1/6 )2
64x3/2 y 1/3
(y 1/6 )2
4(x−3/4 )−2
9
(d) Simplify
p
3
250x10 y 8 .
p
p
p
√
√
√
√
√
√
√ p p
√ p
3
3
3
3
3
3
3
250x10 y 8 = 250 x10 3 y 8 = 125 2 x9 3 x 3 y 6 3 y 2 = 5x3 y 2 2 3 x 3 y 2 = 5x3 y 2 3 2xy 2 .
(e) Simplify
s
3
2x6 y 10 z
.
16x5 y
s
3
2x6 y 10 z
=
16x5 y
r
3
xy 9 z
=
8
p √
√
√
√ √
3
y 3 3 xz
y3 3 x 3 z
x 3 y9 3 z
√
=
.
=
3
2
2
8
12. (a) Multiply out: (2x1/2 + x1/3 )(x1/2 − 5x1/3 ).
(2x1/2 + x1/3 )(x1/2 − 5x1/3 ) = 2x − 9x5/6 − 5x2/3 .
√
(b) Multiply out: ( 2x + 5 − 7)2 .
√
√
√
( 2x + 5 − 7)2 = (2x + 5) − 14 2x + 5 + 49 = 2x + 54 − 14 2x + 5.
√
√
(c) Multiply out: ( x + 1 + x + 4)2 .
√
√
√
√
√
√
( x + 1 + x + 4)2 = (x + 1) + 2 x + 1 x + 4 + (x + 4) = 2x + 5 + 2 x + 1 x + 4.
13. Simplify the following complex numbers, writing each result in the form a + bi:
(a) i43 .
i43 = i42 · i = (i2 )21 · i = (−1)21 · i = (−1) · i = −i.
(b) (4 + 5i)(3 − 2i).
(4 + 5i)(3 − 2i) = 4(3 − 2i) + 5i(3 − 2i) = 12 − 8i + 15i − 10i2 = 12 + 7i + 10 = 22 + 7i.
(c)
1
.
3 + 4i
(d) 3i +
2i
.
4 + 5i
3i +
3i +
(e)
1
3 − 4i
3 − 4i
3 − 4i
3
4
1
=
·
=
=
=
− i.
3 + 4i
3 + 4i 3 − 4i
(3 + 4i)(3 − 4i)
9 + 16
25 25
2i
4 − 5i
2i(4 − 5i)
8i − 10i2
8i − 10(−1)
2i
= 3i +
·
= 3i +
= 3i +
= 3i +
=
2
4 + 5i
4 + 5i 4 − 5i
(4 + 5i)(4 − 5i)
16 − 25i
16 − 25(−1)
10 + 8i
10 + 8i
41 10 + 8i
123i 10 + 8i
10 + 8i + 123i
10 + 131i
= 3i +
= 3i ·
+
=
+
=
=
.
16 + 25
41
41
41
41
41
41
41
3 − 2i
.
5 + 7i
15 − 31i + 14(−1)
3 − 2i 5 − 7i
15 − 10i − 21i + 14i2
1 − 31i
3 − 2i
=
=
·
=
=
.
5 + 7i
5 + 7i 5 − 7i
25 − 49i2
25 − 49(−1)
74
10
(f)
i
3
−
.
4 + i 3 + 2i
3
12 − 3i 3i + 2
i
3
4−i
i
3 − 2i
12 − 3i 3i − 2i2
−
=
−
=
·
−
·
=
−
=
4 + i 3 + 2i
4 + i 4 − i 3 + 2i 3 − 2i
16 − i2
9 − 4i2
16 + 1
9+4
13(12 − 3i) 17(3i + 2)
156 − 39i 34 + 51i
122 − 90i
12 − 3i 3i + 2
−
=
−
=
−
=
.
17
13
13 · 17
13 · 17
221
221
221
14. What is wrong with the following computation?
p
√
√
√
“ − 1 = i2 = −1 · −1 = (−1) · (−1) = 1 = 1”
p
√
√
The third equality −1 · −1 = (−1) · (−1) is not valid. In general,
√
√ √
a · b 6= ab
if a and b are both negative.
15. The area of a rectangle is 84 square miles. The length is 4 miles less than 3 times the width. Find the
dimensions.
Let L be the length and let W be the width.
The area is 84 square miles: 84 = LW .
The length is 4 miles less than 3 times the width: L = 3W − 4.
Substitute L = 3W − 4 into 84 = LW and multiply out:
84 = 3W 2 − 4W.
84 = (3W − 4)W,
Solve for W :
84
− 84
0
0
3W
−
÷
3W
3
W
=
3W 2
−
4W
=
=
3W 2
−
(3W + 14)(W − 6)
4W
+ 14 =
14
=
0
14
−14
3
14
= −
3
ւ
−
84
84
ց
W −6 = 0
W
= 6
14
is ruled out, because the width of a rectangle can’t be negative.
W =−
3
W = 6 gives L = 3W − 4 = 3 · 6 − 4 = 14. The width is 6 miles and the length is 14 miles.
16. The length of a rectangle is 2 less than 3 times the width. The area is 176. Find the dimensions of the
rectangle.
Let L be the length and let W be the width.
The area is 176, so 176 = LW .
11
The length is 2 less than 3 times the width: L = 3W − 2.
Plug L = 3W − 2 into 176 = LW :
176 = (3W − 2)W
176 = 3W 2 − 2W
0 = 3W 2 − 2W − 176
Apply the quadratic formula:
√
√
2 ± 4 + 2112
2 ± 2116
2 ± 46
−44
W =
=
=
=
6
6
6
6
or 8.
−44
W =
doesn’t make sense, because a width can’t be negative. Therefore, the solution is W = 8.
6
The length is L = 3W − 2 = 22.
17. The sum of two numbers is 5. The sum of their reciprocals is
45
. Find the two numbers.
44
Let x and y be the two numbers.
The sum of two numbers is 5: x + y = 5.
45 1
1
45
The sum of their reciprocals is
: + =
.
44 x y
44
45 1
1
45
From x + y = 5, I get y = 5 − x. Plug this into
: + =
:
44 x y
44
1
45
1
+
=
.
x 5−x
44
Clear denominators and simplify:
1
1
45
+
=
x 5−x
44
1
1
= 44x(5 − x) ·
+
44x(5 − x)
x 5−x
1
1
= 44x(5 − x) ·
44x(5 − x) · + 44x(5 − x) ·
x
5−x
44(5 − x) + 44x = 45x(5 − x)
45
44
45
44
220 − 44x + 44x = 225x − 45x2
220 = 225x − 45x2
44 = 45x − 9x2
9x2 − 45x + 44 = 0
Apply the quadratic formula:
x=
45 ±
√
√
45 ± 441
45 ± 21
2025 − 1584
=
=
.
18
18
18
45 + 21
66
11
11
4
=
=
, which gives y = 5 −
= .
18
18
3
3
3
24
4
4
11
45 − 21
=
= , which gives y = 5 − =
.
x=
18
18
3
3
3
4
11
In either case, the two numbers are and
.
3
3
x=
12
18. Calvin and Bonzo, eating together, can eat 540 rib sandwiches in 6 hours. Eating alone, Calvin can eat
240 rib sandwiches in 4 hours less than it takes Bonzo, eating alone, to eat 240 rib sandwiches. How long
does it take Calvin, eating alone, to eat 240 rib sandwiches?
Let x be Calvin’s rate in sandwiches per hour, let y be Bonzo’s rate in sandwiches per hour, and let t
be the time it takes Calvin to eat 240 rib sandwiches.
hours
Calvin and Bonzo
6
Calvin
t
Bonzo
t+4
·
sandiwches per hour
=
sandwiches
·
x+y
=
540
·
x
=
240
·
y
=
240
240
.
t
240
The third equation says y(t + 4) = 240, so y =
.
t+4
The first equation says
6(x + y) = 540, so x + y = 90.
The second equation says xt = 240, so x =
Plug x =
240
240
and y =
into x + y = 90 and solve for t:
t
t+4
240
240
+
= 90
t
t+4
240
240
= 90t(t + 4)
t(t + 4)
+
t
t+4
240(t + 4) + 240t = 90t(t + 4)
240t + 960 + 240t = 90t2 + 360t
480t + 960 = 90t2 + 360t
0 = 90t2 − 120t − 960
0 = 3t2 − 4t − 32
(In the last step, I divided everything by 30.) Solve using the Quadratic Formula:
t=
Since t must be positive,
4±
√
√
4 ± 400
4 ± 20
16 + 384
=
=
.
6
6
6
4 − 20
is ruled out. The answer is
6
t=
4 + 20
= 4.
6
19. Solve the following quadratic equations:
(a) (x − 4)2 = 25.
(x − 4)2 = 25
x − 4 = ±5
x − 4 = 5 gives x = 9. x − 4 = −5 gives x = −1.
13
The solutions are x = 9 and x = −1.
(b) (2x − 3)2 = −16.
(2x − 3)2 = −16
2x − 3 = ±4i
√ √
√
√
−16 by −16 = 16 −1 = 4i.)
3 + 4i
3 − 4i
2x − 3 = 4i gives 2x = 3 + 4i, or x =
. 2x − 3 = −4i gives 2x = 3 − 4i, or x =
.
2
2
3 ± 4i
.
The solutions are x =
2
(I simplified
(c) x2 + 4x + 1 = 0.
Use the quadratic formula:
√
√ √
√
√
−4 ± 12
−4 ± 4 3
−4 ± 2 3
=
=
=
= −2 ± 3.
x=
2
2
2
2
√
√
The roots are x = −2 + 3 and x = −2 − 3.
(d) x2 − 6x + 25 = 0.
−4 ±
√
16 − 4
Use the quadratic formula:
x=
6±
√ √
√
√
36 − 100
6 ± −64
6 ± 64 −1
6 ± 8i
=
=
=
= 3 ± 4i.
2
2
2
2
The roots are x = 3 ± 4i.
(e) 10x2 + 18 = 27x.
10x2 + 18 = 27x
10x2 − 27x + 18 = 0
Apply the quadratic formula:
x=
x=
27 ±
√
√
729 − 720
27 ± 9
27 ± 3
=
=
.
20
20
20
27 + 3
3
27 − 3
6
3
6
= and x =
= . The solutions are x = and x = .
20
2
20
5
2
5
(f) x2 − 4x + 29 = 0.
Apply the quadratic formula:
x=
4±
√ √
√
√
4 ± −100
4 ± 100 −1
4 ± 10i
16 − 116
=
=
=
= 2 ± 5i.
2
2
2
2
(g) x2 + 2x = −10.
x2 + 2x = −10
x2 + 2x + 10 = 0
Apply the quadratic formula:
x=
−2 ±
√ √
√
√
−2 ± −36
−2 ± 36 −1
−2 ± 6i
4 − 40
=
=
=
= −1 ± 3i.
2
2
2
2
14
20. Solve for x:
√
(a) x − 3 = x + 3.
Square both sides and multiply out:
x−3=
√
x+3
√
(x − 3) = ( x + 3)2
2
x2 − 6x + 9 = x + 3
x2 − 7x + 6 = 0
(x − 1)(x − 6) = 0
The possible solutions are x = 1 and x = 6.
Check: For x = 1,
x − 3 = 1 − 3 = −2,
For x = 6,
x − 3 = 6 − 3 = 3,
The only solution is x = 6.
√
√
(b) x + 12 − x = 2.
√
√
x + 3 = 1 + 3 = 2.
√
x+3=
√
6 + 3 = 3.
√
√
x + 12 − x = 2
√
√
x + 12 = x + 2
√
√
( x + 12)2 = ( x + 2)2
√
x + 12 = x + 4 x + 4,
√
8=4 x
√
2= x
√
4 = ( x)2
x=4
Check: x = 4 gives
√
x + 12 −
The solution is x = 4.
√
(c) x + 2 = 7x + 2.
√
x=
√
√
16 − 4 = 4 − 2 = 2.
√
(x + 2)2 = ( 7x + 2)2
x2 + 4x + 4 = 7x + 2
x2 − 3x + 2 = 0
(x − 1)(x − 2) = 0
The possible solutions are x = 1 and x = 2.
Check: If x = 1,
x + 2 = 1 + 2 = 3,
If x = 2,
x + 2 = 2 + 2 = 4,
√
√
7x + 2 = 7 + 2 = 3.
√
7x + 2 =
The solutions are x = 1 and x = 2.
15
√
14 + 2 = 4.
(d)
√
√
√
x + 3 + x + 11 = 2x + 20.
√
√
√
( x + 3 + x + 11)2 = ( 2x + 20)2
√
√
x + 3 + 2 x + 3 x + 11 + x + 11 = 2x + 20
√
√
2x + 14 + 2 x + 3 x + 11 = 2x + 20
√
√
2 x + 3 x + 11 = 6
√
√
x + 3 x + 11 = 3
√
√
( x + 3 x + 11)2 = 32
(x + 3)(x + 11) = 9
x2 + 14x + 33 = 9
x2 + 14x + 24 = 0
(x + 2)(x + 12) = 0
The possible solutions are x = −2 and x = −12.
Check: If x = −2,
√
√
x + 3 + x + 11 = 1 + 3 = 4 and
√
2x + 20 = 4.
If x = −12, both sides of the equation are undefined.
The only solution is x = −2.
21. Solve the following equations for x. (Complex number solutions are allowed.)
(a) x10 − x5 − 2 = 0.
Write the equation as (x5 )2 − x5 − 2 = 0. Let y = x5 .
(x5 )2 − x5 − 2 = 0
y2 − y − 2 = 0
(y − 2)(y + 1) = 0
The possible solutions are y√= 2 and y = −1.
y = 2 gives x5 = 2, or x
= 5 2. And y = −1 gives x5 = −1, or x = −1.
√
5
The solutions are x = 2 and x = −1.
(b) (x − 5)2 − 7(x − 5) − 8 = 0.
Let y = x − 5.
(x − 5)2 − 7(x − 5) − 8 = 0
y 2 − 7y − 8 = 0
(y − 8)(y + 1) = 0
The possible solutions are y = 8 and y = −1.
y = 8 gives x − 5 = 8, or x = 13. And y = −1 gives x − 5 = −1, or x = 4.
The solutions are x = 13 and x = 4.
(c) x4 − 5x2 − 14 = 0.
Write the equation as
Let y = x2 .
(x2 )2 − 5x2 − 14 = 0.
y 2 − 5y − 14 = 0
(y − 7)(y + 2) = 0
16
The possible solutions are y =
√ 7 and y = −2.
√
y = 7 gives x2 = 7, or x √
= ± 7. And y√= −2 gives x2 = −2, or x = ±i 2.
The solutions are x = ± 7 and x = ±i 2.
22. (a) Show that no matter what k is, the following equation has complex roots:
x2 − 4x + (k2 + 5) = 0.
The discriminant is
b2 − 4ac = 16 − 4(k2 + 5) = 16 − 4k2 − 20 = −4 − 4k2 .
Since k2 is nonegative, −4k2 is always less than or equal to 0. Therefore, −4 − 4k2 is negative. Since
the discriminant is negative no matter what k is, the equation always has complex roots.
(b) For what value or values of p does the equation 2x2 − px + 50 = 0 have exactly one root?
The discriminant is
b2 − 4ac = p2 − 400.
The equation has exactly one root when the discriminant is 0:
p2 − 400 = 0
p2 = 400
p = ±20
The equation has exactly one root when p = 20 or p = −20.
23. Find the distance from (3, −4) to (7, 1).
p
√
√
distance = (3 − 7)2 + (−4 − 1)2 = 16 + 25 = 41.
24. Find the center and radius of the circle
x2 + 6x + y 2 − 14y = 6.
2
6
= 32 = 9.
2
2
−14
To complete the square in y, I need to add
= (−7)2 = 49.
2
So I get
x2 + 6x + 9 + y 2 − 14y + 49 = 6 + 9 + 49
To complete the square in x, I need to add
(x + 3)2 + (y − 7)2 = 64
√
The center is (−3, 7) and the radius is 64 = 8.
25. Find the center and radius of the circle
x2 + 3x + y 2 − 4y = 6.
17
2
3
9
To complete the square in x, I need to add
= .
2
4
2
−4
= (−)2 = 4.
To complete the square in y, I need to add
2
So I get
9
9
x2 + 3x + + y 2 − 4y + 4 = 6 + + 4
4
4
2
49
3
+ (y − 2)2 =
x+
2
4
r
3
7
49
The center is − , 2 and the radius is
= .
2
4
2
Patience is needed with everyone, but first of all with ourselves. - Saint Francis de Sales
c 2008 by Bruce Ikenaga
18