Download Document

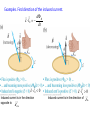
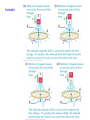
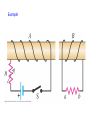
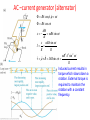
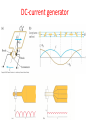
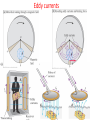
Lectures 16-17 (Ch. 29)
Electromagnetic Induction
1. The law of EM induction
2. The Lenz’s rule
3. Motional emf:
slide wire generator,
Faraday’s disc dynamo,
Ac and dc current generators
Electromagnetic Induction, 1830-1832
Change of magnetic flux through the
loop of wire induces current (i.e. emf)
in the loop.
Michael Faraday (1791-1867)
Joseph Henry (1797-1878)
Law of EM Induction (Faraday’s law)
 
 B   B  dA   B cos dA   B dA
d B
A
A
A
 
dt [ ]  1T 1m2  1Wb (weber )
B
Wilhelm Weber (1804 – 1891)
Flux can be changed by change of B or A or angle between B and dA.
In order to find the direction of the induced current it is convenient to write the
faraday’s law in the form
 
  l0  

in the loop
d B where l0 is the unite vector of a circulation

which direction is connected with dA by a RHR:
dt
It is convenient to choose

dA
 
in such direction that B  dA  0

dA

l0
Examples. Find direction of the induced current.
 
d B
  l0  
dt

l0

l0
 
 l0  0
Induced current is in the direction

opposite to l
0
 
 l0  0

Induced current is in the direction of l0
Lenz’s law
Magnetic field produced by induced
current opposes change of magnetic flux
Heinrich Lenz (1804 –1865)
Examples
Example
Motional emf
Slide-wire generator
 
d B
dA
  l0  
 B
dt
dt
dA  lvdt
 
  l0   Blv
Origin of this emf is in separation of charges
in a rod caused by its motion in B.

 
Fm  qv  B
 
a
Fm  dl
 
q
b
  
   ( v  B )  dl
a
b
  vBl
Motional emf exists in the
conductor moving in B.
It does not require the existence
of the closed circuit.
The secondary magnetic force



Fm '  I  Bl
m
’
External force is required to keep
constant velocity of the rod


 
Fext  Fm '  I  Bl
2
2
(
vBl
)
Pel  I 2 R 

R
R
dW
dx

(vBl ) 2
Pmech 
 Fext
 IBlv  Blv 
dt
dt
R
R
Example. Find motional emf in the rod.
I
V
d
L
Example. Find induced current in the
loop with resistance R.
V
I
Example
A single rectangular loop of wire with the dimensions inside a region of B=0.5 T and part is outside the
field. The total resistance of the loop is 0.2Ω . The loop is pulled from the field with a constant
velocity of 5m/s.
1)What is the magnitude and direction of the induced current?
2) In which part of the loop an induced emf is developed?
3) Find the force required to pull the loop at a constant velocity.
4) Explain why such force is required.
0.1m
0.75m
B
0.5m
x
v
Example
Find emf in each side of the loop and the net emf when
the loop is the region:
a) all inside the region of B
b) partly outside of this region
c) all outside of this region
B=1T
x
40cm
v=2cm/s
30cm
Faraday’s disk dynamo
R
  
BR 2
   v  B  dr  B  rdr 
2
0
0
R
v  r
F’m
+
Fm
v
AC –current generator (alternator)
  BA cos  ,   t
  BA cos t
d
 BA sin t
dt
 BA sin t
I 
R
R
  
B 2 A2 sin 2 t
    B  IAB sin t 
R
Induced current results in
torque which slows down a
rotation. External torque is
required to maintain the
rotation with a constant
frequency.
 
DC-current generator
Applications
2007 Nobel Prize in Physics
For the discovery of the giant magnetic resistance
Big R
B
Peter Grünberg Albert Fert
Tiny magnetic field
triggers large change
in electrical resistance.
Small R
B
I
Resistance strongly depends on the direction of the spin in the first ferromagnetic
layer. When it is the same as in the next ferromagnetic layer R is small, when it’s
opposite to it R is big.
Better read-out heads for pocket-size
devices: miniaturization of PC, ipods, etc.
Eddy currents
Meisner’s effect
Eddy currents responsible for levitation
and Meisner effect in superconductors
S
N
v
Bind
B0
Eddy currents limit efficiency of transformers
Induced nonelectrostatic electric field
dI
0
dt
d B
 
dt
Origin of emf? No motion, moreover no B outside
solenoid, i.e. in the region of a wire loop. Then it
should be E which results in induced current.
dI
0
dt


Fel  dl
d B
 q     dt


 
Fel  qE ,  Fel  dl  0
Nonconcervative force
 
d B
 E  dl   dt
 
Nonelectrostatic field
E

d
l

0

B(t) should induce E by independently on the presence of the loop of the wire!
Let’s find E(r).
 
d B
 E  dl   dt
1.r  R
dB
E 2r  r
dt
B  ni,   K m  0
2
R
E
n di
2 dt
2) r  R
E
r
dB
E 2r  R
dt
n di R 2
E
2 dt r
2
r
R
Displacement current
dB/dt produces E. Let’s show that dE/dt produces B!
Consider the process of charging the capacitor.
Calculate B in front of the plate of capacitor at r>R.
1
 
 B  dl  0 I encl
2
line
Using the plane surface 1 we get
B 2r  0ic
Using the bulging surface 2 we get
B2r  0
We come to contradiction! What is wrong ?
q  CV , C 
0 A
, V  Ed , q   0 AE
d
i
dq
dE
d E
dE
ic 
 0 A
 0
 id , jd  d   0
dt
dt
dt
A
dt
 
 B  dl  0 (ic id )
1.Now we get the same answer for both surfaces 1 and 2!
2. B≠0 between the plates!
General form of Amper’s law
 
d E
 B  dl   (i  dt )
μ= Kmμ0, ε=Kε0,
In free space K=1, Km =1
Let’s find B between the plates.
1.r  R
r2
B 2r   0 jd r   0ic 2
R
id
ic
jd   2
A R
i r
B 0c 2
2 R
2.r  R
B 2r   0id
2
B
r
R
0ic
B
2r
Maxwell’s equations
Two Gauss’s laws + Faraday’s law +Amper’s law
  qencl
 E  dA  
 B  dA  0
 
d B
 E  dl   dt
 
d E
 B  dl   (iencl  dt )
James Clerk Maxwell
(1831 –1879)
Maxwell introduced displacement current, wrote these four equations together,
predicted the electromagnetic waves propagating in vacuum with velocity of light and
shown that light itself is e.m. wave.
1865 Maxwell’s theory
1887 Hertz’s experiment
1890 Marconi radio (wireless communication)