* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download W6 Slides - HixsonEd
Survey
Document related concepts
Transcript
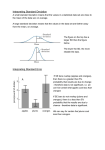
Statistics II Freshman Engineering Clinic II Course Reminders & Deadlines • Pathfinder ▫ Before exercises (on Intellectual Property) due by 10:30 am Wed. March 1st • 3D Game Lab ▫ 2nd deadline of 700 XP midnight Fri. March 10th • Heart Lung Project ▫ Re-write of Literature Review due by Mon. February 27th Review of Last Class – Key Concepts • Statistics I ▫ Area under the bell curve always equals 1 ▫ More similar your data the larger the peak of the bell curve ▫ Z-statistic is used to determine probabilities with normally distributed populations 𝑋−𝜇 𝑍= 𝜎 Review of Last Class – Example Problem • Porphyrin is a pigment in blood protoplasm and other body fluids that is significant in body energy and storage. In healthy Alaskan brown bears, the amount of porphyrin in the bloodstream (in mg/dl) has approximate normal distribution with a mean of 38 mg/dl and a standard deviation of 12. What proportion of these bears have between 27.5 and 67.5 mg/dl porphyrin in their bloodstream? ▫ Z1 = (67.5-38)/12 = 2.46; Probability from Z-table = 0.9931 ▫ Z2 = (27.5-38)/12 = -0.875; Probability from Z-table = 0.1908 ▫ Final answer = 0.9931-0.1908 = 0.8023 Class Overview ▫ Mean, Median, Variance, Standard Deviation, Standard Error ▫ 95% Confidence Interval (C.I.) ▫ Error Bars ▫ Comparing Means of Two Data Sets Basic Stats Review Using the data to the left, calculate the following: (NTU) 1 3 3 6 8 10 • • • • • Mean Median Variance Standard Deviation Standard Error 95% Confidence Interval (C.I.) for Mean • A 95% C.I. is expected to contain the population mean 95 % of the time (from 100 samples, 95 will contain population mean if expressed as x ± 95% C.I. ) X ± (t 95%,n -1)(sX ) • t95%,n-1 is a statistic for 95% C.I. from sample of size n ▫ In EXCEL: t95%,n-1 = TINV(0.05,n-1) Where 0.05 = (100-95)/100 & n = sample size For a sample size of 6, t95%,5 = TINV(0.05, 5) = 2.57 ▫ If n ≥ 30, then t95%,n-1 ≈ 1.96 (Normal Distribution) Mean (NTU) 1 3 3 6 8 10 ± Confidence Interval X ± (t 95%,n -1)(sX ) X ± 2.57*1.4 NTU = 5.2 NTU ± 3.6 NTU Note: 95% confidence intervals is typically larger than +/- standard error interval Filter Example Determine the 95% C.I. for each filter Turbidity Data Test 1 Test 2 Test 3 NTU NTU NTU Filter 1 2.1 2.1 2.2 Filter 2 3.2 4.4 5 Filter 3 4.3 4.2 4.5 Error Bars • Show data variability on plot of mean values • Types of error bars include: Max/min, ± Standard Deviation, ± Standard Error, ± 95% C.I. • “Significant Difference” Using Error Bars to compare data • Standard Deviation ▫ Demonstrates data variability • Standard Error ▫ If bars overlap, any difference in means is not statistically significant ▫ If bars do not overlap, indicates nothing! • 95% Confidence Interval ▫ If bars overlap, indicates nothing! ▫ If bars do not overlap, difference is statistically significant • We’ll use 95 % CI by default ▫ Any time you have 3 or more data points, determine mean, standard deviation, standard error, and t95%,n-1, then plot mean with error bars showing the 95% confidence interval • But if you want to conclude samples are the same or different, you have to use the right error bar! Standard Error Bars No overlap: cannot be sure that the difference is statistically significant. Overlap: can be sure that the difference is not statistically significant. Confidence Interval Error Bars Mean ± 95% C.I., n = 5 No overlap: Can be sure that the difference is statistically significant. Mean ± 95% C.I., n = 5 Overlap: Can not be sure that the difference is not statistically significant. Adding Error Bars to an Excel Graph • Create Graph ▫ Column, scatter,… • Select Data Series • In Layout Tab-Analysis Group, select Error Bars • Select More Error Bar Options • Select Custom and Specify Values and select cells containing the t95%, n 1 s X values Example 1: 95% CI Turbidity Data 1 2 3 mean St Dev NTU NTU NTU NTU NTU 2.1 2.1 2.2 2.1 0.06 3.2 4.4 5 4.2 0.92 4.3 4.2 4.5 4.3 0.15 Filter 1 Filter 2 Filter 3 7.0 6.0 Turbidity (NTU) 5.0 4.2 4.3 Filter 2 Filter 3 4.0 3.0 2.1 2.0 1.0 0.0 Filter 1 Portable Water Filter n 3 3 3 St-Err NTU 0.03 0.53 0.09 t95%,2 +/- 95% CI t95%,2St-Err 4.30 4.30 4.30 0.14 2.28 0.38 Key Takeaways: • • • • • How to calculate confidence intervals How to read the t-test chart How to calculate variance How to calculate standard error Difference between error bars with standard error and confidence interval • What confidence interval means Review: Measures of Central Tendency Mean = x = (NTU) 1 3 3 6 8 10 åx i n = (1 + 3 + 3 + 6 + 8 + 10) / 6 = 5.2 NTU Median = m = Middle number Rank 1 2 3 4 5 6 Number 1 3 3 6 8 10 For even number of sample points, average middle two = (3+6) NTU/2 = 4.5 NTU Excel: Mean – AVERAGE; Median - MEDIAN Variability • Variance, s2 ▫ sum of the square of the deviation about the mean divided by degrees of freedom s 2 x-x) å ( = 2 i n -1 • Example (cont.) s2 = [(1-5.2)2 + (3-5.2)2 + (3-5.2)2 + 6-5.2)2 + (8-5.2)2 + (10-5.2)2] /(6-1) = 11.8 NTU2 Excel: Variance – VAR Standard Deviation, s s s 2 • Square-root of variance • If phenomena follows Normal Distribution (bell curve), 95% of population lies within 1.96 standard deviations of the mean • Error bar is s Normal Distribution above & below mean 95% Excel: standard deviation – STDEV -4 -1.96 -2 0 1.96 2 Standard Deviations from Mean Standard Deviation 4 Standard Deviation s s 2 s = s = 11.8 NTU 2 2 = 3.43 NTU Standard Error of Mean sX • Also called St-Err • For sample of size n taken from population with standard deviation estimated as s s sX n estimate↓, i.e., estimate of population • As n ↑, sxbar mean improves • Error bar is St-Err above & below mean Standard Error s sX n s sX = = 3.43 NTU / 6 =1.4 NTU n