Download scientific-notation-pdf

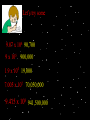
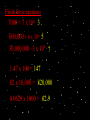
Scientists use easy ways to write large numbers.
This easy way is more compact & more useful.
This compact, useful method is called
To write a number in Scientific Notation, express it as a
product of two factors
There are 2 criteria for writing a number in Scientific
Notation:
Criteria:
a. One factor is a number GREATER than or EQUAL to 1, but
LESS than 10. (This will usually be a decimal)
b. The other factor is a POSITIVE POWER of 10.
Let’s look at an example:
93,000,000
Notice that the
decimal point is
moved until it
reaches a
number greater
than 1, but less
than 10.
How many times was the decimal point moved to the left?
That answer is your exponent.
93,000,000 in Scientific Notation is: 9.3 x 107
Steps:
1. Move the decimal point to the LEFT until you
get to a number greater than or equal to 1, but less
than 10.
2. Count the number of places moved- that is the
power of 10.
Another example:
185,000
1.85 x 105
Let’s try some:
120,000 1.2 x 105
4,064,000 4.064 x 106
25,000
2.5 x 104
714,500 7.145 x 105
8
1.56
x
10
156,000,000
How would you reverse Scientific Notation (write in
standard form)?
Do the OPPOSITE.
1. Move the decimal point the number of places as the
exponent in the Power of 10 to the RIGHT.
2. Add 0’s as place fillers.
3.6 x 103
3,600
Let’s try some
9.07 x 104 90,700
9 x 105 900,000
1.9 x 104 19,000
7.005 x 107 70,050,000
9.415 x 108 941,500,000
Scientific Notation can also be used to rename
large decimals that are between 0 & 1
These numbers will use negative exponents for their
powers of 10.
Follow these rules:
Let’s look at an example:
0.00064=
6.4 x 10-4
1. First factor is greater than
1, but less than 10.
2. Second factor is a power
of 10 with a negative
exponent. The exponent
depends on how many
times you moved the
decimal to the RIGHT.
Here’s another example:
0.0815 =
You try some:
0.015 = 1.5 x 10-2
0.0000086= 8.6 x 10-6
0.000124= 1.24 x 10-4
0.0069= 6.9 x 10-3
8.15 x 10-2
0.00000079 = 7.9 x 10-7
0.0000716 = 7.16 x 10-5
0.0045 = 4.5 x 10-3
It is now your turn to explain how to write numbers in
scientific notation. Explain the process of scientific
notation to the person next to you. Explain it using whole
numbers & decimal between 0 & 1. Pretend that your
partner does not understand this process, so explain it
well & with examples!
Finish these equations
7000 = 7 x 10n
600,000 = 6 x 10n
30,000,000 = 3 x 10n
1.47 x 100 =
82 x 10,000 =
0.0629 x 1000 =
Finish these equations
7000 = 7 x 10n 3
600,000 = 6 x 10n 5
30,000,000 = 3 x 10n 7
1.47 x 100 = 147
82 x 10,000 = 820,000
0.0629 x 1000 = 62.9