* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Topology Group
Grothendieck topology wikipedia , lookup
General topology wikipedia , lookup
Covering space wikipedia , lookup
Homotopy groups of spheres wikipedia , lookup
Orientability wikipedia , lookup
Topological data analysis wikipedia , lookup
Fundamental group wikipedia , lookup
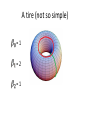
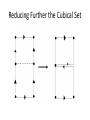
Homology Not to be confused with: • • • • Homeomorphism Homomorphism Homotopy Or any other “homo-type” math concept I have left out • Oh, and it is NOT the mixing of the cream and skim milk Application and Theory • For the purpose of this project we are trying to use Homology to analyze granular flow, specifically the force chains. One way to do this is by computing the Betti numbers • We also want to be able to understand the inner workings of CHomP and how the Betti numbers are computed. • Homology is a branch of math in Algebraic Topology • It uses Algebra to find topological features (invariants) of topological spaces specifically we will be dealing with cubical sets • “…Allows one to draw conclusions about global properties of spaces and maps from local computations.” (Mischaikow) Defining the Homology group • The vector spaces are called the kchains for X • Boundary operator: This is a map defined as follows • We call an element of the k-chains a cycle if for and • An element is called a boundary if there exists such that Defining the Homology group • So finally we define the homology group as • (a.k.a ) • Example: Explanation of what Betti Numbers are Corollary: Any finitely generated abelian group G is isomorphic to a group of the form Where r is a nonnegative integer, denotes the group of integers modulo b, , provided k > 0, and divides . The numbers r and the b’s are uniquely determined by G . And the number is the rank of subgroup and is called the of G. What do the homology groups tell us about Topological Spaces ? The Homology groups measure the number of k-dimensional “holes” • - in 0 dimensions the holes are connected components • - in 1 dimension we get tunnels • - in 2 dimensions we get cavities Examples • What are the Betti numbers of this space? Homology =8 = 5 =0 More Examples = 12 = 10 =0 A tire (not so simple) =1 =2 =1 What the Betti numbers??? = I don’t know We Need an Algorithm Which Can Compute the Complex Structures of the previous Example: • There is an algorithm which uses SmithNormal Form but it is too inefficient • So we turn to using this idea of reducing before computing the Homology • Namely Elementary Collapses and Acyclic Reduction Elementary Collapses Acyclic Reduction: Chomp • An set is acyclic if is isomorphic to if k=0, and otherwise zero. • Namely this means it has trivial homology • The Main Idea is to compute the homology of the reduced set X, which is called the relative homology with an acyclic subset of X Shaving Process • This is accomplished by “Shaving” where in removable cubes are removed from the original set X • Algorithms using Shaving are fast, so it should be used first as an initial reduction Showing the Algorithm in Action Reducing Further the Cubical Set Questions?