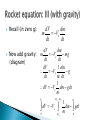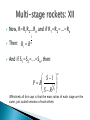Download Propulsion systems

Spring 2011: [F&S, Chapter 6]
Q; What velocity, v, do I need to just escape the gravitational pull of
the planet? (the escape velocity).
A: Think about the energies involved!
Initial state:
1 2
mv
Kinetic energy = 0 (planet) +
2
Gravitational potential energy =
GMm

r
Final state:
Kinetic energy = 0 (planet) + 0 (spacecraft)
GMm
0
Gravitational potential energy = 

Initial state energy must equal final state energy

1 2 GMm
mv 
 00
Therefore:
2
r
1 2 GMm
mv 
2
r
1 2 GM
v 
2
r
2GM
2
v 
r
2GM
LEARN THIS DERIVATION
v
AND THE FINAL EQUATION!
r
Conceptually
 The various phases of a space mission from
‘concept’ through to ‘end-of-life’ phase.
 An appreciation of some of the details of each of
these phases and how financial, engineering and
science constraints etc. affect mission design.
 How a spacecraft’s environment changes from
ground level, near earth orbit and deep space.
 How these environments (radiation, thermal, dust
etc.) feedback into the final mission design.
Mathematically



Understand how to use the drag equation to
work out the force on a body as it travels
through the atmosphere
Calculate the solar constant for Earth and
(other bodies) making justifiable
assumptions.
Derive the escape velocity of a body.
Spring 2011: [F&S, Chapter 6]

4 major tasks:
1. Launch
2. Station/trajectory acquisition
3. Station/trajectory keeping (staying where it
should be, or going in the correct direction).
4. Attitude control (pointing in the correct direction)
Launch
 Need lift-off acceleration, a, to be greater
than gravitational acceleration, g. (“a>g”) for
an extended period.
 This implies a very high thrust for a long
duration. E.g., the shuttle main engine: 2 x
106 N for 8 minutes.
 Typical Δv ≥ 9.5 km s-1 (including drag and
gravity losses).
Launch phase (continued)
 Still difficult to achieve with current
technology
 Only achievable with chemical rockets
 Massive launch vehicles required for relatively
small payloads
 Major constraint for spacecraft and mission
design is the mass cost: £1000s - £10,000s
per kilogram.
Station/trajectory acquisition
 Apogee motors (apogee = ‘furthest point’)
◦ Orbit circularisation
◦ Inclination removal
◦ Requires a force of ~75 kN for 60 seconds. Δv = 2
km s-1.

Perigee motors (perigee=‘nearest point’)
◦
◦
◦
◦
Orbit raising
Payload Assist modules (‘PAM’)
Interial Upper Stages (‘IUS’)
Δv ~4.2 km s-1 (30° inclination parking orbit ->
equatorial geostationary).
Earth Escape
 Δv ~ 7.6 km s-1 (Mars flyby)
 Δv ~ 16 km s-1 (Solar system escape velocity)
◦ Without using gravity assist manoeuvres.
Station/trajectory keeping
 Low thrust levels required (mN – 10s N)
pulsed for short durations.
 Δv ~ 10s – 100s m s-1 over duration of
mission.
Attitude control (‘pointing’)



Very low thrust levels for short duration
Small chemical rockets
Reaction wheels (diagram).
Principle of operation of all propulsion systems is
Newton’s third law
“...for every action, there is an equal and opposite
reaction...”
Derivation: Need to balance exhaust (subscript
‘e’) momentum with rocket momentum.
∑momenta = 0 (Conservation of linear momentum)
(Recall: momentum = mass x velocity)
∴ m dV = -dm Ve
dV = -Ve dm/m
So, now some maths...
V
m
•dm is the mass ejected
dm
V dV  Ve m m
o
o
 V   Ve ln m
V
Vo
m
mo
V  Vo  Ve [ln m  ln mo ]
V  Vo  Ve ln mo  ln m
 mo 
V  Vo  Ve ln  
m
•dV is the increase in speed due
to the ejected mass (dm)
•Ve is the exhaust velocity (ie. the
velocity of the ejected mass
relative to the rocket)
•m is the rocket mass (subscript
‘o’ denotes initial values)
In practice, drag reduces Vmax by
~0.3 – 0.5 km s-1.
Tsiolkovsky’s Equation (the rocket equation).


Recall (in zero g):
dV
dm
m
 Ve
dt
dt
dV
dm
Now add gravity: m
 Ve
 mg
dt
dt
(diagram)
dV
1 dm

 Ve
g
dt
m dt
1
 dV  Ve dm  gdt
m
mo  m f
Vs
 dV  V 
e
0
mo
tB
1
dm   gdt
m
0
Integrating previous equation:
mo  m f
Vs
tB
1
dm   gdt
m
0
 dV  V 
e
0
mo
Vs  Ve ln m
 gt B
  m
o
Vs  Ve ln 

  mo  m f

  gt B



mo  m f
mo

Vs  Ve ln mo  ln mo  m f   gt B

Define R as:
•Vs =spacecraft velocity
•Ve= exhaust velocity
•gs = accl. of gravity acting
on spacecraft
•tB = rocket burn time
•mf= mass of fuel
R’ is the “effective mass ratio
mo
R
mo  m f
Vs  Ve ln R  g s t B
Ve g s t B
Vs  Ve ln R 
Ve

  g s t B 

Vs  Ve ln  R  exp 
 Ve 

Vs  Ve ln R
  g stB 

R  R  exp 
 Ve 




Therefore, want a short burn time as possible
to minimise gravitational losses.
Gravitational losses reduce V by ~1 km s-1
This conflicts with the requirements to reduce
drag effects at low atmosphere (low speed at
low altitude)
Resolve conflict by using non-vertical ascent.
ge = net downward accl.
= gravity - centrifugal
Retarding gravitational force = ge cos θ

Typical launch sequence:
◦ Lift-off (straight up!)
◦ Clear tower
◦ Roll to correct heading
◦ Pitch to desired trajectory
◦ Recall space shuttle launch sequence. Rolls and
pitches almost immediately after clearing tower.
Reason to minimise loss dues to drag and gravity!

Assume a single stage, liquid propellant
chemical rocket.
◦ Fuel – kerosene
◦ Oxidiser – liquid oxygen
◦ Typical of fuel used for Atlas, Thor, Titan and
Saturn rockets.
Ve ~2.5 km s-1, assume mass: 20% structure, 80% fuel
Recall,
 mo
R
m m
f
 o

5


(In this case)
Vmax  Ve ln R  4
km s-1
•Compare with Earth’s escape velocity ~ 11 km s-1!
•Velocity required for 300 km altitude Earth orbit
~7.8 km s-1.
•Taking into account drag and gravity losses implies a
required Vmax ≥ 9.3 km s-1
•Best performance from a fully cryogenic fuel system
get Vmax ~9.5 km s-1.
SOLUTION: Multi-Staging!

Parallel staging
◦ Partially simultaneous operation (e.g. Space Shuttle)

Series staging
◦ Sequential operation (e.g. Ariane, Saturn V etc.)

Principle: jettison inert mass to reduce load
for subsequent rocket stages.
Stage velocity, Vs = Vmax – Vo = Ve ln R = -Ve ln (1-R)
Stage velocity, Vs = Vmax – Vo = Ve ln R = -Ve ln (1-R)
Jettisoning structure from stage ‘n’ increases R (the
mass ratio) and thus Vs for the subsequent stages,
n+1, n+2 etc.
However, since Vs ∝ ln R, improvement is slow with
R
Assume a simple rocket where:
 mf = mass of propellant
 ms = mass of structure
mo
mo
 mp = mass of payload
R

m p  ms mo  m f
 mo = mf + ms + mp
mo
 Define mass ratio, R:
P
mp
 Payload ratio,
P:
 Structure ratio,
S:
m f  ms
mf
S
 1
ms
ms
 S 1 
 P  R

SR

Assume a liquid propellant chemical rocket.
◦ Fuel – kerosene
◦ Oxidiser – liquid oxygen
◦ Typical of fuel used for Atlas, Thor, Titan and
Saturn rockets.
Ve ~2.5 km s-1, assume: 1t structure, 8t fuel, 1t
payload
Recall definition of payload ratio, R
 mo
R
m m
f
 o
  1  1  8   10 

     5

  (1  1  8)  8   2 

(In this case)
Now calculate the payload ratio, P and the
structure ratio, S.
Recall: mo = 1 + 8 +1= 10, mf = 8, ms = 1 tons.
mo 10
P

 10
mp 1
mf
8
S  1
 1  9
ms
1
mo
10
R

5
m p  ms 1  1
m0  m f  m p  ms
R
mo
m p  ms
P
mo
mp
S
m f  ms
ms
 1
 S 1 
 P  R

S R
mf
ms
For our kerosene rocket:
Ve ~ 2.5 km s-1 , R =5
Recall, Vs = Ve ln R = 2.5 x ln 5 ~ 4 km s-1
∴ Vs = 4 km s-1 – suborbital!

Now consider this 10 ton rocket to be a
payload (i.e. a stage) of a larger rocket…

Therefore, assume that the mass/fuel ratio is the
same for the second stage, and thus we can use
the same ratios (ie, this stage is just a scaled up
version of the original stage):
∴ mp= 10t and thus,
mo= P x mp = 10 x 10t = 100t
Now our 1 ton original payload can reach:
4 + 4 = 8 km s-1 – orbital, just…
using a 100t rocket!


Now consider this 100 ton rocket to be a
payload (i.e. a stage) of an even larger
rocket…
Therefore, assume that the mass/fuel ratio is
the same for the previous stage, and thus we
can use the same ratios:
∴ mp= 100t and thus,
mo= P x mp = 10 x 100t = 1000t
Now our 1 ton original payload can reach:
4 + 4 + 4= 12 km s-1 – escape velocity
using a 1000t rocket!
Therefore a 3-stage kerosene rocket can put a
payload into orbit, and reach Earth escape
velocity, whereas a single stage could not!
In general:
◦ Vmax = ∑Vs
Maximum rocket velocity is the total of the stage
velocities.
Using conventional definitions (i.e. 1st stage is the
first to burn etc.), the payload ratio of the ith stage
is, Pi:
m
Pi 
oi
moi1
(ie. The payload ratio of stage 1 = mass of stage 1/ mass of stage 2)
Thus the total payload ratio, P is:
mo1
P
 P1P2 P3  Pn
mp
The structural payload, S is:
Si 
m fi  msi
msi
And the mass ratio, R is:
moi
Ri 
moi  m fi
V  V ln R 

Therefore, Vmax 

And if all stages have the same Ve
s
ei
i
Vmax  Ve  ln Ri 
Vmax  Ve ln R1  ln R2   ln Rn 
Vmax  Ve ln R

R  R1 R2 R3  Rn
(Generally, however, this is not the case)
Stage
Propellant
Ve
(km s-1)
mf
(tons)
ms
(tons)
thrust
(tons wgt)
burn time
(secs)
1st
Kerosene + O2
2.32
2160
140
3400
150
2nd
H2(l) + O2(l)
4.10
420
35
450
390
3rd
H2(l) + O2(l)
4.25
100
10
90
480
1st Stage
2nd Stage
3rd Stage
14.40
1.08
0.21
moi
2965
665
210
Ri
3.69
2.72
1.91
Pi
4.46
3.16
2.10
Vsi (km s-1)
3.03
4.10
2.75
Fuel consumption (tons/sec)
For a payload, mp, of 100 tons

Note high thrust of 1st stage
High efficiency of stages 2 and 3
P for a 3 stage kerosene rocket ~90
P for the Saturn V ~ 30 (more efficient).

Such a rocket could lift:



100 tons into a low earth orbit
40 tons into earth escape (i.e. to the moon)
1 ton payload to Mars!
For Apollo, the Saturn V lifted the Command module to
LEO.
◦ The command module went to the moon and back.
◦
◦
◦
◦
Optimisation of number of stages:
Q: What is the optimum number of stages?
Theoretically...recall:
P=payload ratio
R=mass ratio
S=structure ratio
 S 1 
P  R

S R
P  P1 P2 P3  Pn
R  R1 R2 R3  Rn
 Si  1 

Pi  Ri 
 S i  Ri 
 S1  1  S 2  1 

 
 P  R1 R2  
 S1  R1  S 2  R2 

Now, R=R1R2...Rn and if R1=R2=...=Rn
1
n

Then: Ri  R

And if S1=S2=...=Sn, then:
 S 1 

P  R
1 
SR n 
n
(Effectively all this says is that the mass ratios of each stage are the
same, just scaled versions of each other).




Optimisation of number of stages involves
minimising P
∴ want to minimise:  S  1 


1


n
SR 
∴want to maximise 1/n, i.e., n→∞.
Q: Why don’t we see systems with very large
numbers of small stages?

Each stage requires:
◦
◦
◦
◦
◦



Engine and nozzles
Ignition mechanism
Separation mechanism
Fuel pumps (for liquid propellants)
Small stages have worse P, R and S.
Therefore greater cost and complexity
Thus a ‘trade-off’.
‘n=3’ is usually the maximum number of
stages (some ‘n=4’, but rare).
Because the Earth revolves on its axis from
West to East once every 24 hours (86400
secs) a point on the Earth’s equator has a
velocity of 463.83 ms-1.
Reason: radius of the Earth, RE = 6.3782 x 106
metres.
Earth’s circumference = 2πRE = 4.007 x 107 m
Equatorial velocity = 4.007 x 107 / 86400 =
463.83 ms-1



Therefore, a spacecraft launched eastwards
from the Earth’s equator would gain a free
increment of velocity of 463.83 ms-1.
Away from the equator the Earth has a
smaller circumference which is determined by
multiplying the equatorial circumference by
the cosine of the latitude in degrees.
For example, the Russian Baikonur
Cosmodrome is at 45° 55’ north. The Earth’s
rotational velocity at that point is: 322.69 m
s-1.

System classification:

Function:
◦ Various possible schemes (see F&S, Fig. 6.1)
◦ Other ‘exotic’ systems possible
◦ “Primary propulsion” – launch
◦ “Secondary propulsion”
 Station/trajectory acquisition and keeping
 Attitude control

Recall: vastly different requirements for different
purposes:
◦ ΔV of m s-1 – km s-1
◦ Thrust of mN – MN
◦ Accelerations of μg - >10g

Different technologies applicable to different
functions/regimes.

Principle:
◦ Combustion of propellants at high pressure in a
small confined volume produces high temperature
gas.
◦ Expansion through nozzles convert random thermal
energy to directed kinetic energy: “thrust”.

Propellants:
◦ And fuel and oxidiser undergoing exothermic
reaction producing gaseous products.

Considerations:
◦ Specific energy content, rate of heat release,
storage, handling, etc.

Chemical rocket types:
◦ Solid propellant
◦ Liquid propellant
◦ Hybrid (usually solid fuel and a liquid oxidiser)

Solid propellant rockets:
◦
◦
◦
◦
◦
Oldest rocket technology – Chinese 12th Century.
Very simple – no moving parts (nozzles?)
Only needs an igniter and a douser
Fuel stored in combustion chamber
Relatively cheap
Solid propellant rockets (continued)
 Advantages:
◦
◦
◦
◦

Simple and cheap
Reliable
High thrust
High energy density propellant thus small volume
Disadvantages:
◦ Only limited throttling
◦ Generally only single burn (a firework effectively).
Solid propellant rockets (continued)
 Propellant is a fuel and oxidiser matrix with
aluminium powder regulator.
 Cast directly into casing of rocket
 Thrust is proportional to burn rate
 “Cigarette mode” – long duration, low thrust
because of small combustion area.
 Axial ignition used to increase burn area and
increase thrust.
Solid propellant rockets (continued)
 Burn area and thrust defined by ‘grain’, produced
by the mandrel during casting of the fuel.
 This gives a limited amount of “preprogrammed” throttling of the propellant.
 Ignition is via a pyrotechnic device which ignites
the propellant in the igniter. Axial burn.
 Applications:
◦ Early launch vehicles (missiles)
◦ Launch vehicle strap-on boosters (e.g. Titan, Ariane,
Shuttle)
◦ Secondary propulsion
Liquid propellant rockets
 First flight 16th March 1926.
◦ Robert Goddard using liquid oxygen and gasoline






Max altitude = 12.5 metres
Flight time = 2.5 seconds
Engine thrust ~ 40 N
Vmax ~ 96 km/hour
Landed 56 metres from launch site
Advantages
◦ Long burn time
◦ Controllability




Throttling
On-off-on operation
Emergency shutdown
Redundant systems
Liquid propellants (continued)
 Disadvantages
◦ Complexity and reliability
◦ Cost
◦ Mass

Requirements
◦ Separate storage of fuel and oxidiser remote from
combustion chamber
◦ Thus need propellant pump and feed system
◦ Chamber injector and mixer
◦ Igniter, combustion chamber and exit nozzle



Liquid propellants
◦
◦
◦
◦
◦
(Kerosene/ethanol) + liquid oxygen + N2O4
Monomethyl hydrazine (‘MMH’)
Unsymmetrical dimethyl hydrazine (‘UDHM’)
Aerozine50 (50/50 mix of hydrazine and UDMH)
Liquid hydrogen and liquid oxygen (cryogenic
propellants)
Some combinations require ignition, others
(known as ‘hypergols’) are self-igniting as soon
as the fuel + oxidiser mix (e.g. Aerozine50 and
N2O4).
Applications
◦ Most modern launch vehicles
◦ Secondary propulsion systems



Manned spacecraft, mainly reusable (unlike
Ariane)
Expensive “launch vehicle”
Designed to be multi-purpose
◦
◦
◦
◦
◦
Laboratory (‘Spacelab’)
Recovery repair and return of satellites
Space station servicing
Launch of satellites
Just about to be retired!

Primary propulsion system, two elements:
◦ External fuel tanks feeding SSME (‘Space Shuttle
Main Engines’, x3)
◦ Two solid rocket strap-on boosters
 Burn for 120 seconds, separate, parachute into ocean
300 km downrange for recovery and reuse.
◦ SSMEs use closed cycle combustion with a chamber
pressure of 207 Bar (20.7 GPa) and a burn time of
480 seconds
◦ 100% thrust ~2.1 x 106 N.
◦ External fuel tank jettisoned (and burns up) pre
orbital insertion.





The space shuttle combines liquid and solid
propellants.
Solid propellants give a lower ‘specfic impulse’
(thrust per mass of propellant) but are compact,
simple and stable.
Once ignited it burns continuously. Thrust can
only be controlled by varying the burn area.
The liquid propellant in the STS combines
hydrogen and oxygen and can be throttled to
vary the thrust.
The STS uses 2 SRBM (‘Solid Rocket Booster
Motors’) and the liquid propellant in the main
external tank during launch.
Thrusters (secondary propulsion units).
 Once in space there is still a need for thrust.
 There are two main types:
◦ Sustained high thrust for orbital manoeuvring etc.
◦ Low thrust for atitude control (rotate the spacecraft, or
to controls its spin rate etc.)

Cold gas thrusters
◦ Take an inert gas (nitrogen or argon) stored at high
pressure and connected to a series of valves.
◦ The thrusters are arranged off-axis to control
spin/rotation.
◦ Specific impulse is low with low volumes of gas
◦ Typical thrust ~10 mN in short bursts.
Monopropellant
 The decomposition of hydrazine (N2H4)
generates heat.
 Expansion of the hot gas through nozzles
produces a specific impulse.
 Hydrazine is a liquid between 275 – 387 K
and is held under pressure in tanks.
 Can provide ~10 N for orbital control and
station keeping.
Bi-propellant
 E.g. MMH/nitrogen tetroxide
 Propellants burn on contact
 They are mixed in the thruster/apogee motor
and can provide sustained thrust.
 Can be used for orbital rising as well as
atitude control.
 Provides precise amounts of thrust on
demand.
Solid propellant apogee motors
 To launch into GEO etc. usually launch to a
LEO and then boost with a final stage burn.
 To achieve a high, circular orbit at apogee,
need a high thrust, short duration burn
 Usually provided by a solid propellant apogee
motor.
 For a GEO satellite of 1000 kg need 900 kg of
propellant and a ΔV of ~2 km s-1.
 Burn for 40-60 seconds with an average
thrust of 50 – 75 kN
Shuttle external tank
and SRBs
The characteristic feature of the SRB’s thrust
curve’s profile is the period of reduced thrust
(to about 70% of max. 50 secs. into the flight)
giving a ‘sway-backed’ appearance (below).
Its purpose is to reduce the thrust while the
shuttle is passing through the region of
maximum dynamic pressure. This is when the
product of velocity and air pressure is a
maximum and when the possibility of
damage by aerodynamic forces is greatest.
Therefore minimise risk by reducing thrust for
a short period.


Another term sometimes seen is the ‘thrust
impulse’, Is.
It is simply defined as:
Ve
IS 
g

And has units of “seconds”. The larger IS the
greater the effective thrust (recall Ve is the
exhaust velocity).
Amount of thrust generated is proportional to
exposed (burning) surface area of propellant.
Cross-sections of various solid propellant castings
and associated thrust profiles.