* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 7.1 Apply the Pythagorean Theorem
History of mathematics wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
Location arithmetic wikipedia , lookup
Vincent's theorem wikipedia , lookup
List of important publications in mathematics wikipedia , lookup
John Wallis wikipedia , lookup
Wiles's proof of Fermat's Last Theorem wikipedia , lookup
Nyquist–Shannon sampling theorem wikipedia , lookup
Central limit theorem wikipedia , lookup
Fermat's Last Theorem wikipedia , lookup
Brouwer fixed-point theorem wikipedia , lookup
Four color theorem wikipedia , lookup
Proofs of Fermat's little theorem wikipedia , lookup
Fundamental theorem of algebra wikipedia , lookup
Fundamental theorem of calculus wikipedia , lookup
Mathematics and architecture wikipedia , lookup
History of trigonometry wikipedia , lookup
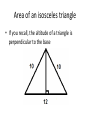
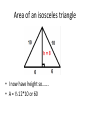
7.1 Apply the Pythagorean Theorem Parts of a Right triangle • Hypotenuse – opposite the right angle and the longest side • Legs – the sides that form the right angle Pythagorean Theorem • The theorem says that of I square the legs of a right triangle and add them they will be equal to the hypotenuse squared Pythagorean Theorem • 𝑎2 +𝑏 2 =𝑐 2 A couple of examples solved Pythagorean triples • A Pythagorean triple are integers(whole numbers) that exactly fit the Pythagorean theorem. The simplest of which is 3,4,5 where 3 and 4 are legs and 5 is the hypotenuse A list of some of the Pythagorean triples Finding the area of an isosceles triangle • In the figure below, finding are is easy! A = 1/2bh • A = ½ 12*6 • A = 36 Area of an isosceles triangle • In this figure it requires a little more thought! • How do I find Height? Area of an isosceles triangle • If you recall, the altitude of a triangle is perpendicular to the base Area of an isosceles triangle • In an isosceles triangle, an altitude from the vertex angle will bisect the opposite side • Do you see two right triangles! Area of an isosceles triangle • I can now use the Pythagorean theorem to solve for the height • 62 + ℎ2 = 82 can be written as 82 − 62 =ℎ2 Area of an isosceles triangle • I now have height so……. • A = ½ 12*10 or 60 Area of a composite figure Notice the figure is made of a rectangle and two right triangles I need to find the are of the square and at least one of the triangles Use the Pythagorean theorem to find the other side of the rectangle Composite figure • Find the missing side of the rectangle using Pythagorean theorem • 26+18+18 = 62 • 302 − 182 = 576 • 24 is the square root of 576 • Find the area of the rectangle • Find the area of the two triangles • 24*26+2(1/2*18*24) = 432𝑚2 is the area