* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Recovered File 1
Financial economics wikipedia , lookup
Greeks (finance) wikipedia , lookup
Rate of return wikipedia , lookup
Investor-state dispute settlement wikipedia , lookup
Pensions crisis wikipedia , lookup
Business valuation wikipedia , lookup
Credit rationing wikipedia , lookup
Financialization wikipedia , lookup
Internal rate of return wikipedia , lookup
International investment agreement wikipedia , lookup
Interest rate swap wikipedia , lookup
Continuous-repayment mortgage wikipedia , lookup
Investment management wikipedia , lookup
Interest rate ceiling wikipedia , lookup
Credit card interest wikipedia , lookup
History of investment banking in the United States wikipedia , lookup
Land banking wikipedia , lookup
History of pawnbroking wikipedia , lookup
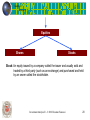
Investment Analysis II MGMT-6330 Investment Analysis II Interest Rates, Forwards and Futures Investment Analysis II - © 2012 Houman Younessi 1 Investment Analysis II Interest and Interest Rates (perhaps a review) Interest is the fee paid by the borrower to the lender for the possession of an asset for a fixed period of time. Interest is usually calculated in terms of the percentage of monetary value of the asset for a specific period of time (e.g. a year). This is called an interest rate. In investment finance we define interest rate as the relative return of “risk-free” securities. Investment Analysis II - © 2012 Houman Younessi 2 Investment Analysis II Interest Rate Calculation Simple Time Independent interest (usually simply called interest) is the pure difference between the purchase price of the debt (the amount the borrower must pay at maturity) and the face value of the amount borrowed at contract time (principal) presented as a percentage with respect to the face value. Example: I borrowed $100 from my son and have agreed to pay him $110 “when he needs his money back”. What is the interest? Answer: Maturity time is “when he needs his money back”, it is fixed but not a constant. The interest is the pure difference the principal and purchase price: 110 100 0.1 10% 100 Note: Such interest is not time based. He may ask for his money back in ten years (his loss) or tomorrow (mine) Investment Analysis II - © 2012 Houman Younessi 3 Investment Analysis II Interest Rate Calculation Simple Time Normalized Interest (usually called simple interest RATE) is the difference between the purchase price of the debt (the amount to pay at maturity) and the face value of the amount borrowed at contract time (principal) when the time from contract to maturity is fixed and predetermined; presented as a percentage of the face value. Example: I borrowed $100 from my son and have agreed to pay him $110 in exactly one year. What is the interest rate? Answer: Maturity time is exactly one year, it is fixed and constant. The interest rate still is the pure difference the principal and purchase price: P(t m) P(t 0) 110 100 0.1 10% P(t 0) 100 per annum Note: Such interest rate is now time based. He can now only ask for his money back in exactly one year Investment Analysis II - © 2012 Houman Younessi 4 Investment Analysis II Interest Rate Calculation What if he wanted his money sooner, or I wanted to borrow the money for longer than one year ? There should be no problem. The interest rate may be calculated for any period of time. These periods usually range from a day (overnight) to multiple years (30 year loan). Each rate is calculated exactly the same. Example: I borrowed $100 from my son and have agreed to pay him $110 in exactly 3 months. What is the interest rate? P(t m) P(t 0) 110 100 0.1 10% P(t 0) 100 Per Quarter Note: the numerical value of the rate is the same, but the actual rate is not the same. This is 10% every three months Investment Analysis II Interest rate calculation What if he offered to lend me the money at 2.5% a quarter or 10% per annum, which deal should I take? There is no difference. P(t m) P(t 0)(1 r ) P(t m) P(t 0) r P(t 0) rP(t 0) P(t m) P(t 0) P(t m) P(t 0)(1 r ) P(t 90) 100(1 0.025) 102.5 100 2.5 So: P(t 180) 100(1 0.025) 102.5 100 2.5 P(t 270) 100(1 0.025) 102.5 100 2.5 P(t 360) 100(1 0.025) 102.5 100 2.5 $2.5 Per Quarter x 4 Quarters = $10 Per Annum Note: I am not paying interest on the interest. I am borrowing $100, keeping it for 3 with the $2.50 interest; then borrow $100 again, keep it months, then return it along for 3 months, then return it along with the $2.5 interest………(a total of four times) Investment Analysis II Interest Rate Calculation What if he realized that if I kept the money for a whole year and return the principal and interest at the end of the year, at the end of the 3rd month, he is actually lending me $102.5 and at therefore at the end of the 6th month I have $102.5 (1+0.025)= $105.06 of his money and I should pay interest on that sum for the third quarter and so on. At what effective annual rate have I borrowed the $100? This is called Compound Interest P(t m) P(t 0)(1 r ) or in general: P(t 90) 100(1 0.025) 102.5 P(t 180) 102.5(1 0.025) 105.06 P(t 270) 105.6(1 0.025) 107.68 P(t m) P(t 0)(1 r1)(1 r2 )(1 r3 )....(1 rn ) r (1 r1 )(1 r2 )(1 r3 )....(1 rn ) (1 rn )n P(t 360) 107.68(1 0.025) 110.38 Note: Now I am paying interest on interest and as such end up paying $0.38 more Investment Analysis II Time Value of Money (Present and Future Value) Because the notion of interest exists, money now, would be worth more than money in the future (if interest rates are assumed to be more than zero). One very good way of evaluating the value of various different payment patterns is to determine their present value. The better investment (ceteris paribus) is the one with a higher present value If we know the interest rate, in a simple situation, the present value is the future value divided by (1+r). So d=1/(1+r) is called the discount factor. In the case of payments at a future different from a year, the rate is expressed in its equivalent annual rate (r). If the payment takes place in 1/n years, 1 using simple interest rule the discount factor is: d The compound version is: (1 r / n) 1 d (1 r ) Investment Analysis II - © 2012 Houman Younessi 1 n 8 Investment Analysis II Investment Analysis II - © 2012 Houman Younessi 9 Investment Analysis II What personal characteristics must board members have? They must be: Competent – But know the limits of theory Confident – But not overly so Controlled (in control of their biases) – But not robots also helps if they are: Connected (informed of what is going on and able to exert some influence) But not corrupt Investment Analysis II - © 2012 Houman Younessi 10 Investment Analysis II Over-confidence Most people are over-confident, we are probably wired that way We tend to take credit for our successes and blame our failures on others or on bad luck Investment Analysis II - © 2012 Houman Younessi 11 Investment Analysis II In terms of trading, this means: Most people over-trade (have higher turn-over than necessary) Even if you were right in selling A and buying B (usually not the case with over-confident investors), the trading fees will kill you In the long-run, you lose more than you need to for the same amount of return intended Most people take on more risk than necessary Investment Analysis II - © 2012 Houman Younessi 12 Investment Analysis II Causes of over-confidence: Illusions of : Choice Knowledge Task familiarity Outcome sequence Availability of technology Active involvement Past success Investment Analysis II - © 2012 Houman Younessi 13 Investment Analysis II So, what have we learned? You are not as good as you think you are The world is not as simple as you think it is XXXXX Investment Analysis II - © 2012 Houman Younessi 14 Investment Analysis II So, what must we do? We must: Know the theory and tools Know ourselves Know others Know the environment Know the market Investment Analysis II - © 2012 Houman Younessi 15 Investment Analysis II Theory and tools QUIZ Investment Analysis II - © 2012 Houman Younessi 16 Investment Analysis II Financial Assets Financial Asset: Current or future ability to purchase Three forms: Cash: Immediate or near immediate purchasing instrument Contracts: A financial right or obligation set not necessarily through a document Securities: A document that confers upon its owner a financial claim Note: Cash is arguably a form of security Investment Analysis II - © 2012 Houman Younessi 17 Investment Analysis II Financial Assets Securities Fixed Income Cash Contract Equities Fixed income: instruments that pay a fixed amount of money to their owners Equity: A security that confers to its owner the right to a part of and a corresponding portion of profits of an economic concern. An equity is sometimes called a share Investment Analysis II - © 2012 Houman Younessi 18 Investment Analysis II Fixed Income Bonds … Money-Market Accounts Savings Accounts Bond: A security purchased by its owner called the creditor; at an agreed amount called the bond price that gives the owner the right to a fixed, pre-determined payment called the nominal value (or face value, par vale or principal); at a future, predetermined date called the maturity date (or simply maturity). Investment Analysis II - © 2012 Houman Younessi 19 Investment Analysis II Equities Shares Stocks Stock: An equity issued by a company called the issuer and usually sold and traded by a third party (such as an exchange) and purchased and held by an owner called the stockholder. Investment Analysis II - © 2012 Houman Younessi 20 Investment Analysis II Contracts Simple Contracts Derivatives Derivative: A contract whose payoff depends on the value of another financial variable such as the price of a stock, price or maturity of a bond, an exchange rate, or the price or another feature of another derivative) Investment Analysis II - © 2012 Houman Younessi 21