* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 8 - HCC Learning Web
Equations of motion wikipedia , lookup
Transmission (mechanics) wikipedia , lookup
Virtual work wikipedia , lookup
Coriolis force wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Center of mass wikipedia , lookup
Mitsubishi AWC wikipedia , lookup
Quaternions and spatial rotation wikipedia , lookup
Fundamental interaction wikipedia , lookup
Fictitious force wikipedia , lookup
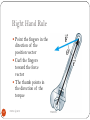
Newton's laws of motion wikipedia , lookup
Centrifugal force wikipedia , lookup
Classical central-force problem wikipedia , lookup
Torque wrench wikipedia , lookup
Centripetal force wikipedia , lookup
Chapter 8 Rotational Equilibrium and Rotational Dynamics Ying Yi PhD 1 PHYS I @ HCC Outline Torque Two conditions for equilibrium Center of Gravity 2 PHYS I @ HCC Torque There are three factors that determine the effectiveness of the force in opening the door: The magnitude of the force The position of the application of the force The angle at which the force is applied 3 PHYS I @ HCC Torque, cont Torque, , is the tendency of object about some axis = r F a force to rotate an is the torque Symbol is the Greek tau F is the force r is the length of the position vector SI unit is N.m 4 PHYS I @ HCC Direction of Torque Torque is a vector quantity The direction is perpendicular to the plane determined by the position vector and the force If the turning tendency of the force is counterclockwise, the torque will be positive If the turning tendency is clockwise, the torque will be negative 5 PHYS I @ HCC Multiple Torques When two or more torques are acting on an object, the torques are added As vectors If the net torque is zero, the object’s rate of rotation doesn’t change 6 PHYS I @ HCC Example 8.1 Battle of the revolving Door Two disgruntled businesspeople are trying to use a revolving door, as in Figure 8.3. The woman on the left exerts a force of 625 N perpendicular to the door and 1.20 m from the hub’s center, while the man on the right exerts a force of 8.5×102 N perpendicular to the door and 0.800 m from the hub’s center. Find the net torque on the revolving door. 7 PHYS I @ HCC Group problem: Revolving door A businessman enters the same revolving door on the right, pushing with 576 N of force directed perpendicular to the door and 0.700 m from the hub, while a boy exerts a force of 365 N perpendicular to the door, 1.25 m to the left of the hub. Find (a) the torques exerted by each person and (b) the net torque on the door. 8 PHYS I @ HCC General Definition of Torque The applied force is not always perpendicular to the position vector The component of the force perpendicular to the object will cause it to rotate 9 PHYS I @ HCC General Definition of Torque, cont When the force is parallel to the position vector, no rotation occurs When the force is at some angle, the perpendicular component causes the rotation 10 PHYS I @ HCC General Definition of Torque, final Taking the angle into account leads to a more general definition of torque: = r F sinƟ F is the force r is the position vector Ɵ is the angle between the force and the position vector 11 PHYS I @ HCC Lever Arm The lever arm, d, is the perpendicular distance from the axis of rotation to a line drawn along the direction of the force d = r sin Ɵ This also gives t = rF sin Ɵ 12 PHYS I @ HCC Right Hand Rule Point the fingers in the direction of the position vector Curl the fingers toward the force vector The thumb points in the direction of the torque 13 PHYS I @ HCC Net Torque The net torque is the sum of all the torques produced by all the forces Remember to account for the direction of the tendency for rotation Counterclockwise torques are positive Clockwise torques are negative 14 PHYS I @ HCC Example 8.2: The swinging door (a) A man applies a force of F=3.00×102 N at an angle of 60.0º to the door of Figure 8.7a, 2.00 m from the hinges. Find the torque on the door, choosing the position of the hinges as the axis of rotation. (b) suppose a wedge is placed 1.50 m from the hinges on the other side of the door. What minimum force must the wedge exert so that the force applied in part (a) won’t open the door? 15 PHYS I @ HCC Torque and Equilibrium First Condition of Equilibrium The net external force must be zero F 0 or Fx 0 and Fy 0 This is a necessary, but not sufficient, condition to ensure that an object is in complete mechanical equilibrium This is a statement of translational equilibrium 16 PHYS I @ HCC Torque and Equilibrium, cont To ensure mechanical equilibrium, you need to ensure rotational equilibrium as well as translational The Second Condition of Equilibrium states The net external torque must be zero 0 17 PHYS I @ HCC Selecting an Axis The value of depends on the axis of rotation You can choose any location for calculating torques It’s usually best to choose an axis that will make at least one torque equal to zero This will simplify the torque equation 18 PHYS I @ HCC Equilibrium Example The woman, mass m, sits on the left end of the seesaw The man, mass M, sits where the see-saw will be balanced Apply the Second Condition of Equilibrium and solve for the unknown distance, x 19 PHYS I @ HCC Axis of Rotation If the object is in equilibrium, it does not matter where you put the axis of rotation for calculating the net torque The location of the axis of rotation is completely arbitrary Often the nature of the problem will suggest a convenient location for the axis When solving a problem, you must specify an axis of rotation Once you have chosen an axis, you must maintain that choice consistently throughout the problem 20 PHYS I @ HCC Example 8.3 Balancing act A woman of mass m=55.0 kg sits on the left end of a seesaw a plank of length L=4.00 m, pivoted in the middle as in figure 8.8. (a) First compute the torques on the seesaw about an axis that passes through the pivot point. Where should a man of mass M=75.0 kg sit if the system (seesaw plus man and woman) is to be balanced? (b) Find the normal force exerted by the pivot if the plank has a mass of mpl=12.0 kg. (c) repeat part (a), but this time compute the torques about an axis through the left end of the plank. 21 PHYS I @ HCC Center of Gravity The force of gravity acting on an object must be considered In finding the torque produced by the force of gravity, all of the weight of the object can be considered to be concentrated at a single point 22 PHYS I @ HCC Calculating the Center of Gravity The object is divided up into a large number of very small particles of weight (mg) Each particle will have a set of coordinates indicating its location (x,y) 23 PHYS I @ HCC Calculating the Center of Gravity, cont. We assume the object is free to rotate about its center The torque produced by each particle about the axis of rotation is equal to its weight times its lever arm For example,1 = m1 g x1 24 PHYS I @ HCC Calculating the Center of Gravity, cont. We wish to locate the point of application of the single force whose magnitude is equal to the weight of the object, and whose effect on the rotation is the same as all the individual particles. This point is called the center of gravity of the object 25 PHYS I @ HCC Coordinates of the Center of Gravity The coordinates of the center of gravity can be found from the sum of the torques acting on the individual particles being set equal to the torque produced by the weight of the object xcg 26 PHYS I @ HCC mi xi mi y i and ycg mi mi Center of Gravity of a Uniform Object The center of gravity of a homogenous, symmetric body must lie on the axis of symmetry Often, the center of gravity of such an object is the geometric center of the object 27 PHYS I @ HCC Experimentally Determining the Center of Gravity The wrench is hung freely from two different pivots The intersection of the lines indicates the center of gravity A rigid object can be balanced by a single force equal in magnitude to its weight as long as the force is acting upward through the object’s center of gravity 28 PHYS I @ HCC Notes About Equilibrium A zero net torque does not mean the absence of rotational motion An object that rotates at uniform angular velocity can be under the influence of a zero net torque This is analogous to the translational situation where a zero net force does not mean the object is not in motion 29 PHYS I @ HCC Solving Equilibrium Problems Diagram the system Include coordinates and choose a rotation axis Isolate the object being analyzed and draw a free body diagram showing all the external forces acting on the object For systems containing more than one object, draw a separate free body diagram for each object 30 PHYS I @ HCC Problem Solving, cont. Apply the Second Condition of Equilibrium This will yield a single equation, often with one unknown which can be solved immediately Apply the First Condition of Equilibrium This will give you two more equations Solve the resulting simultaneous equations for all of the unknowns Solving by substitution is generally easiest 31 PHYS I @ HCC Example 8.6 A weighted forearm A 50.0 N bowling ball is held in a person’s hand with the forearm horizontal, as in Figure 8.13a. The biceps muscle is attached 0.0300 m from the joint, and the ball is 0.350 m from the joint. Find the upward force F exerted by the biceps on the forearm (the ulna) and the downward force R exerted by the humerus on the forearm, acting at the joint. Neglect the weight of the forearm and slight deviation from the vertical of the biceps. 32 PHYS I @ HCC Group Problem: Walking a horizontal beam A uniform horizontal beam 5.00 m long and weighing 3.00×102N is attached to a wall by a pin connection that allows the beam to rotate. Its far end is supported by a cable that makes an angle of 53.0º with the horizontal. If a person weighing 6.00×102 N stands 1.50 m from the wall, find the magnitude of the tension T in the cable and the force R exerted by the wall on the beam. 33 PHYS I @ HCC Homework 1, 2, 4, 7, 10, 20, 21 34 PHYS I @ HCC