* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lock-in amplifiers
Regenerative circuit wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Superheterodyne receiver wikipedia , lookup
Battle of the Beams wikipedia , lookup
Audio crossover wikipedia , lookup
Oscilloscope history wikipedia , lookup
Signal Corps (United States Army) wikipedia , lookup
Telecommunication wikipedia , lookup
Analog television wikipedia , lookup
Opto-isolator wikipedia , lookup
Cellular repeater wikipedia , lookup
Valve audio amplifier technical specification wikipedia , lookup
Analog-to-digital converter wikipedia , lookup
Radio transmitter design wikipedia , lookup
Phase-locked loop wikipedia , lookup
High-frequency direction finding wikipedia , lookup
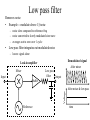
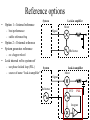
Lock-in amplifiers http://www.lockin.de/ Signals and noise Frequency dependence of noise • Low frequency ~ 1 / f Total noise in 10 Hz bandwidth – example: temperature (0.1 Hz) , pressure (1 Hz), acoustics (10 -- 100 Hz) – example: shot noise, Johnson noise, spontaneous emission noise • Total noise depends strongly on signal freq – worst at DC, best in white noise region • Problem -- most signals at DC log(Vnoise) • High frequency ~ constant = white noise Signal at DC 1/f noise 10 Hz White noise 0 0.1 1 10 100 1kHz log( f ) Noise amplitude Signal at 1 kHz log(Vnoise) White noise log(Vnoise) 1/f noise 1/f noise White noise 10 Hz 0 0 0.1 1 10 100 1kHz log( f ) 0.1 1 10 100 1kHz log( f ) Lock-in amplifiers • Shift signal out to higher frequencies • Approach: • Modulate signal, but not noise, at high freq – no universal technique -- art – example: optical chopper wheel, freq modulation • Detect only at modulation frequency – Noise at all other frequencies averages to zero – Use demodulator and low-pass filter Demodulation / Mixing • • • • Multiply input signal by sine wave Sum and difference freq generated Compare to signal addition -- interference Signal frequency close to reference freq – low freq beat – DC for equal freq sine waves – DC output level depends on relative phase Product Two sine waves Sum Signal freq approaches ref freq • Beat frequency approaches DC as signal freq approaches ref freq Reference Signal freq vs ref freq Mixer outputs 1 1.05 1.1 1.15 1.2 1.25 Phase sensitive detection • Signal freq matches reference freq • Reference = sin(2pft) • Signal = sin(2pft + f) – f is signal phase shift • Product = cos(f) - cos(2pft) DC part Product waveforms -- signal times reference Reference wave Signal phase shift f 0 0.2 p 0.4 p 0.6 p 0.8 p p Low pass filter Removes noise • Example -- modulate above 1/f noise – noise slow compared to reference freq – noise converted to slowly modulated sine wave – averages out to zero over 1 cycle • Low pass filter integrates out modulated noise – leaves signal alone Demodulated signal Lock-in amplifier Mixer After mixer Low pass filter Output Input Buffer Voltage After mixer & low pass Reference time Typical LIA low pass filters • For weak signal buried in noise • Ideal low pass filter blocks all except signal • Approximate ideal filter with cascaded low pass filters Ideal 6 db/oct 12 db/oct log gain 18 db/oct frequency Phase control • • • • Reference has phase control Can vary from 0 to 360° Arbitrary input signal phase Tune reference phase to give maximum DC output Mixer Input Output Reference Phase shift f Reference options • Option 1 -- Internal reference System Lock-in amplifier Mixer – best performance – stable reference freq Signal • Option 2 -- External reference • System generates reference Reference – ex: chopper wheel • Lock internal ref to system ref – use phase locked loop (PLL) – source of name “lock-in amplifier” System Lock-in amplifier Mixer Signal Reference VCO PLL Integrate Analog mixer • Direct multiplication Multiplying mixer – accurate – not enough dynamic range – weak signal buried in noise • Switching mixer – big dynamic range – but also demodulates harmonics Harmonic content of square wave 1 1/3 1/5 1/7 1/9 Switching mixer Switching mixer design • Sample switching mixer • Back-to-back FETs – example: 1 n-channel & 1 p-channel – feed signal to one FET, inverted signal to second FET • Apply square wave to gates – upper FET conducts on positive part of square wave – lower FET conducts on negative part Switching mixer circuit n-channel FET bias source drain gate n p Signal voltage Signals with harmonic content • Option 1: Use multi-switch mixer – approximate sine wave – cancel out first few harmonic signals • Option 2: Filter harmonic content from signal – bandpass filter at input – Q > 100 Lock-in amp with input filter Digital mixers • Digitize input with DAC • Multiply in processor • Advantages: – Accurate sine wave multiplication – No DC drift in low pass filters – Digital signal enhancement • Problems: – Need 32 bit DAC for signals buried in noise – Cannot digitize 32 bits at 100 kHz rates • Digital mixers – Good for slow signals – High signal to noise or low accuracy Lock-in amps in servos • Lock to resonance peak – Servos only lock to zero – Need to turn peak into zero • Take derivative with lock-in Take derivative of lineshape – modulate x-voltage – F(x)-voltage amplitude like derivative • No fundamental • only 2 f signal Use lock-in amp to extract amplitude of F(x) – “DC” part of mixer output – filter with integrator, not low-pass F(x) x Lock-in amps for derivative • Lock-in turns sine wave signal into DC voltage • At peak of resonance – no signal at modulation freq – lock-in output crosses zero Input signal • Discriminant – use to lock F(x) x Zero crossing at resonance Lock-in output (derivative) Fabry-Perot servo • Lock to peak transmission of high Q Fabry-Perot etalon • Use lock-in amp to give discriminant – No input bandpass -- or low Q < 2 • Bandpass rolloff usually 2-pole or greater – No low pass filter -- replace with integrator • Low pass filter removes noise • Need noise to produce correction • Design tips – reference freq must exceed servo bandwidth by factor of ~ 10 – but PZT bandwidth is servo limiter – use PZT resonance for modulation Fabry-Perot Laser PD Acoustic noise LIA reference Sum & HV Digital mixers in servos • May be okay for low precision, medium speed servo – Not for fast servos -- ex: laser frequency stabilization – Not for high accuracy -- ex: laser gyro • Should be excellent for slow servos – Ex: tele-medicine, temperature controllers – Digital processing can compensate for system time delay