Download differential_inductance_IFCC_14june2016_VM (2)

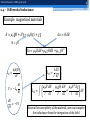
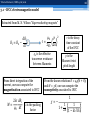
Differential inductance of
superconducting magnets:
the role of coupling currents
Vittorio Marinozzi
CERN, 14/06/2016
Vittorio Marinozzi, CERN 14/06/2016
Outline:
1. Experimental motivation
2. Differential inductance
3. IFCC electromagnetic model
4. Implementation in QLASA
5. Experimental comparison
6. Effects on quench protection
7. Conclusions
2
Vittorio Marinozzi, CERN 14/06/2016
1.1 – Experimental motivation
 Larp tests in 2013
 Fast extraction on dump
resistor 𝑅𝑑
𝑅𝑑 𝑡
 𝐼 = 𝐼0 𝑒 −
𝐿
Using measured inductance, it is impossible to fit the decay,
even at the very beginning!
3
Vittorio Marinozzi, CERN 14/06/2016
1.2 – Experimental motivation
The HQ inductance from exponential fit of the decay beginning is
about 30% lower than the one measured at low ramp rate
4
5
Vittorio Marinozzi, CERN 14/06/2016
1.3 – Experimental motivation
 Same phenomenon seen in LQ tests
 Impossible to justify with quench back, AC losses, current redistribution….
• Too fast
Can the inductance actually change at high ramp rate?
If yes, why?
I want to justify this behavior with coupling currents
effect on differential inductance
6
Vittorio Marinozzi, CERN 14/06/2016
2.1 – Differential inductance
What is the inductance?
𝜙(𝐵)
𝐿𝑠 =
𝐼
𝑑𝐼
𝑒. 𝑚. 𝑓. = −𝐿𝑠
𝑑𝑡
𝐿 = 𝜇0 𝑛2 𝑙𝜋𝑟 2
The inductance of a device depends
only on the geometry!
What happens when the magnetic flux is not linear?
Inductance depends on the current!
𝑑𝐼
𝑒. 𝑚. 𝑓. ≠ −𝐿𝑠
𝑑𝑡
7
Vittorio Marinozzi, CERN 14/06/2016
2.2 – Differential inductance
Faraday-Neumann-Lenz:
𝑑𝜙 𝐵 𝑑𝐼
𝑑 𝐿𝑠 𝐼 𝑑𝐼
𝑉=−
=−
𝑑𝐼 𝑑𝑡
𝑑𝐼 𝑑𝑡
𝑑𝜙 𝐵
𝑉=−
𝑑𝑡
𝑉 = − 𝐿𝑠 +
𝑑𝐿𝑠 𝑑𝐼
𝐼
𝑑𝐼
𝑑𝑡
 It is useful to define a “differential inductance”
𝑑𝐿𝑠
𝑑𝜙(𝐵)
𝐿𝑑 = 𝐿𝑠 +
𝐼=
𝑑𝐼
𝑑𝐼
Such that
𝑑𝐼
𝑉 = −𝐿𝑑
𝑑𝑡
“Standard” inductance and differential inductance are quantities
conceptually different!
Standard inductance is related to
the field flux
Differential inductance is related
to the flux change (voltage)
8
Vittorio Marinozzi, CERN 14/06/2016
2.3 – Differential inductance
Example: iron saturation
“…remember that the inductance is
lower at high current because of
the iron saturation…”
“…remember that the inductance is
larger at low current because of
the iron saturation…”
Because of the iron, the standard
inductance is larger at high current.
Instead, the differential
inductance is larger at low current,
while iron does not affect it at all at
high current!
9
Vittorio Marinozzi, CERN 14/06/2016
2.4 – Differential inductance
Example: magnetized materials
𝐵 = 𝜇0 𝑀 + 𝐻 = 𝜇0 𝐻 1 + 𝜒
𝑑𝑢 = 𝐻𝑑𝐵
𝑀 = 𝜒𝐻
𝑑𝑢 = 𝜇0 𝐻𝑑𝐻+𝜇0 𝜒𝐻𝑑𝐻 +𝜇0 𝜒𝐻2
1 𝑑𝑈
𝐿𝑑 =
𝐼 𝑑𝐼
𝑑𝜙(𝐵)
𝐿𝑑 =
𝑑𝐼
𝑑𝐼
𝑉 = −𝐿𝑑
𝑑𝑡
𝑑𝑈
= −𝑉𝐼
𝑑𝑡
𝐿𝑑 =
𝜇0 𝐻 𝑑𝐻 𝜇0 𝜒𝐻 𝑑𝐻 𝜇0 𝐻2 𝑑𝜒
+
+
𝑑𝑉
𝐼 𝑑𝐼
𝐼 𝑑𝐼
𝐼 𝑑𝐼
Known the susceptivity of the material, one can compute
the inductance from the integration of the field
10
Vittorio Marinozzi, CERN 14/06/2016
3.1 –IFCC electromagnetic model
Extracted from M. N. Wilson “Supercoducting magnets”
𝜇0 𝑝
𝜏=
2𝜚𝑒 2𝜋
𝑑𝐵𝑖
𝐵𝑖 = 𝐵𝑒 −
𝜏
𝑑𝑡
𝜚𝑒 is the effective
transverse resistance
between filaments
From direct integration of the
current, one can compute the
magnetization associated to IFCC
2𝜆𝜏 𝑑𝐵𝑖
𝑀=
𝜇0 𝑑𝑡
𝜆 is the packing
factor
𝜏 is the decay
time constant
of the IFCC
2
𝑝 is the
filament twist
pitch lenght
From the known relations 𝐵 = 𝜇0 𝑀 + 𝐻
and 𝑀 = 𝜒𝐻, one can compute the
susceptivity associated to IFCC
1
𝜒=−
1+
1
1
2𝜆 1 − 𝐵𝑒 𝐵𝑖
11
Vittorio Marinozzi, CERN 14/06/2016
3.2 –IFCC electromagnetic model
A qualitative explanation
We have seen that IFCC can be seen as a magnetization of the coils
It is the same phenomenon that we see with the iron!
Iron makes the
differential inductance
higher at low current.
Then it saturates and it
does not affect the
inductance at all
IFCC are basically
screening currents. They
try to keep the flux
constant. This is why they
make the differential
inductance lower!
12
Vittorio Marinozzi, CERN 14/06/2016
3.3 –IFCC electromagnetic model
Exponential approximation
𝑑𝐵𝑖
𝐵𝑖 = 𝐵𝑒 −
𝜏
𝑑𝑡
𝐵𝑒 = 𝐵0 𝑒 −𝑡 𝜏𝑒
𝐵𝑖 0 = 𝐵𝑒 (0) = 𝐵0
𝜏 is the IFCC decay time
𝜏𝑒 is the transport current decay time
𝜏𝑒 = 𝐿/𝑅
𝑡
𝑡
𝐵0
−
−𝜏
𝐵𝑖 =
𝜏𝑒 − 𝜏𝑒 𝑒 𝜏𝑒
𝜏 − 𝜏𝑒
With a simple assumption, one can find a solution for the field
produced by inter-filament currents
With a simple assumption, one can find an analytical formula
for the susceptivity related to the inter-filament currents
2𝜆𝜏
𝜒(𝑡) =
𝜏𝑒
𝑡
−𝜏
− 𝜏𝑒
𝑡
−𝜏
𝑒 𝑒
𝑡
−𝜏
𝑒 𝑒
−
𝑡
−𝜏
𝑒
− 2𝜆𝜏 𝑒
𝑡
−𝜏
𝑒
−
𝑡
−𝜏
𝑒
V. Marinozzi et al., "Effect of coupling currents on the dynamic inductance during fast transient in
superconducting magnets", Physical Review Special Topics – Accelerators and beams, 2015.
13
Vittorio Marinozzi, CERN 14/06/2016
3.4 –IFCC electromagnetic model
Main issue of the “exponential” model:
We do not want to calculate the new inductance, we want to use it!
𝐵𝑒 = 𝐵0 𝑒 −𝑡
𝜏𝑒
𝜏𝑒 = 𝐿/𝑅 depends on the inductance, therefore it
cannot be used as input.
The current decay depends on the magnet inductance
BUT
The magnet inductance depends on the decay!
 First conclusion: differential inductance of
superconducting magnets is not a
defined value, but it depends on the
current decay, and vice-versa.
Vittorio Marinozzi, CERN 14/06/2016
4.1 –Implementation in QLASA
 QLASA is a software for the simulation of quench
propagation in superconducting magnets.
 Very useful for a simple implementation of the IFCC
model
• It is semi-analytical
• Magnet inductance is an input (not from a BEM-FEM
or similar)
• Inductance can be changed using a simple analytical
formula
I will use the exponential approximation, in
an iterative and step-by-step way
14
15
Vittorio Marinozzi, CERN 14/06/2016
4.2 –Implementation in QLASA
Important assumption: we assume that the
coupling currents do not affect the magnetic field
𝐿𝑑 =
𝜇0 𝐻 𝑑𝐻 𝜇0 𝜒𝐻 𝑑𝐻 𝜇0 𝐻2 𝑑𝜒
+
+
𝑑𝑉 = 𝐿′ + Δ𝐿
𝐼 𝑑𝐼
𝐼 𝑑𝐼
𝐼 𝑑𝐼
We can talk of
inductance variation
𝜇0 𝜒 𝑑
Δ𝐿 =
2𝐼 𝑑𝐼
𝐻2 𝑑𝑉
𝜇0 𝑑𝜒
+
𝐼 𝑑𝐼
𝐻2 𝑑𝑉
Computation of the field integral can be done numerically
16
Vittorio Marinozzi, CERN 14/06/2016
4.3 –Implementation in QLASA
Circuit solution
𝑑𝐼
𝑅𝑑 + 𝑅𝑞 𝐼 + 𝐿 = 0
𝑑𝑡
At each time step, the
quantities are constant
The exponential
approximation can be
used!
Inductance variation is computed
through the susceptivity at each
time step, and used in the following
step as input
17
Vittorio Marinozzi, CERN 14/06/2016
4.4 –Implementation in QLASA
Analytical solution for a costheta quadrupole
𝜇0 𝜒 𝑑
Δ𝐿 =
2𝐼 𝑑𝐼
𝜇0 𝑑𝜒
𝐻 𝑑𝑉 +
𝐼 𝑑𝐼
2
𝑎2
𝐻2 𝑑𝑉
𝑎1
The field integral is limited to the
magnetized material volume, i.e. to the coils
For a quadrupole,
the field in the coils
is analytical and
can be integrated
𝐻2 𝑑𝑉
𝑙𝐽02 𝜋 3 4 𝑎14
𝑎2
𝑎2
𝑎14
2
=
𝑎 −
16 ln
+ ln
+ 4+2
2 64 2 64
𝑎1
𝑎1
𝑎2
With the exponential approximation, and for cos 𝑛𝜗 magnets,
the inductance reduction can be computed analytically, and
can be implemented very easily in any software
18
Vittorio Marinozzi, CERN 14/06/2016
4.5 –Implementation in QLASA
Example: discharge on a dump resistor
We assume that a quadrupole
is short-circuited on a dump
resistor, and that quench
resistance is null
From excel sheet!
We expect an
exponential
decay 𝐼 =
𝐼0 𝑒 −𝑡 𝜏𝑒
We can use:
• Exponential
approximation
• Analytical magnetic
field
• We do not have the
complication of
quench resistance
19
Vittorio Marinozzi, CERN 14/06/2016
5.1 –Experimental comparison
 Comparison with HQ test on
exponential decay
(60 mΩ dump resistor)
 IFCC 𝜏 = 15 ms (average value)
 The model can describe the
decay at the beginning
 In order to describe the whole
decay, one should add coupling
currents power dissipation and
subsequent quench back
Very good agreement!
Vittorio Marinozzi, CERN 14/06/2016
5.2 –Experimental comparison
We can describe a current decay. Is that a proof?
 A current decay is a basically combination of dump
resistor, magnet inductance and quench resistance
 We know very well the dump resistor
 We have understood that we do not know well the
inductance, even if we have measured it at low ramp rate
• Therefore, we do not know the quench resistance!
 We have a model that predicts the inductance, but when
quench resistance begins to become important, the
model cannot be validated
• We know only that the decay time is good if we
describe well the decay, i.e. that the ratio L/R is
good, but we do not have any hint on them
separately
We need to measure inductance and resistance during a quench,
both of them separately
20
21
Vittorio Marinozzi, CERN 14/06/2016
5.3 –Experimental comparison
Inductance measurement during a quench
 You need at least two coils of the magnet with no resistance
• You can extract the inductive voltage
• You can subtract the inductive voltage to the other
coils, in order to obtain the resistive voltage
𝐿𝑐𝑜𝑖𝑙 =
𝑉𝑆𝐶 𝑐𝑜𝑖𝑙
𝐼
Why two coils?
You should have one, but you
have to be sure that it has only
inductive voltage. The easiest
way to be sure is to compare to
another one. If voltages are
identical, you are sure that coils
are superconductive.
𝑅𝑐𝑜𝑖𝑙
𝑉𝑅 𝑐𝑜𝑖𝑙 − 𝐿𝑐𝑜𝑖𝑙 𝐼
=
𝐼
It can be proved that the magnet
inductance is 𝐿 = 𝑁𝑐𝑜𝑖𝑙 𝐿𝑐𝑜𝑖𝑙
This method works only
for identical coils!
22
Vittorio Marinozzi, CERN 14/06/2016
5.4 –Experimental comparison
 Another HQ test
 No dump resistor
 Quench induced by heaters in two
coils
 Again, dynamic effects needed to
describe well the decay
 Coil 15 and 16 are clearly resistive
 Coil 17 and 20 have identical
voltages until about 100 ms
• You can compute inductance
and resistance!
Vittorio Marinozzi, CERN 14/06/2016
5.5 –Experimental comparison
 Good agreement between simulated and experimental
resistance until 100 ms.
• After 100 ms, resistance cannot be measured!
Important conclusion: you can measure magnet resistance
only if you have one (better two) superconducting coils!
23
Vittorio Marinozzi, CERN 14/06/2016
5.6 –Experimental comparison
 The inductance measured during the quench is very different from the
inductance measured at low ramp rate (factor 2!)
 The model of the IFCC allows to describe well the experimental inductance!
Important conclusion: you have to compute the differential
inductance of a magnet case by case. Every quench has
conceptually a different inductance!
24
25
Vittorio Marinozzi, CERN 14/06/2016
5.7 –Experimental comparison
Recent test of QXFS1 at Fermilab
The dynamic effects on differential inductance are needed!
26
Vittorio Marinozzi, CERN 14/06/2016
5.8 –LEDET
 Ledet is the program developed by Emmanuele Ravaioli for the CLIQ simulation
CLIQ exploit coupling
currents in order to
induce quench
Coupling currents cannot
be added as external
source power in the code!
Courtesy of Emmanuele Ravaioli
Similar results with independent, completely
different approach!
Coupling currents are described with
lumped elements (small L-R
circuits), which takes energy from the
main circuit in order to be generated
E. Ravaioli et al., "Lumped-Element Dynamic Electro-Thermal model of a superconducting Magnet", Cryogenics.
27
Vittorio Marinozzi, CERN 14/06/2016
6.1 – Quench protection
Does this study really affects quench
protection analysis?
Nominal (IL+OL PH) MQXF hot spot temperature [K]
Including inductance reduction
Neglecting inductance reduction
~260 K
~285 K
 Neglecting the inductance reduction gives ~25 K more in the MQXF
quench simulation.
 MQXF has high inductance, no dump resistor
• In smaller magnets, with dump resistor, it can be more
• For example, in the first slide quench we have ~40 K
 This model could strongly affect protection study of magnets
Vittorio Marinozzi, CERN 14/06/2016
28
7.1 –Conclusions
 Experimental evidences show that the magnet inductance measured at low ramp
rate cannot be used to describe the current decay.
 An electromagnetic model shows that the IFCC affects the magnet
differential inductance.
 The model can be implemented in a simple analytical way in a quench software.
 The model can describe very well current decays, and it has been
experimentally validated on LARP tests.
 The magnet inductance has been experimentally measured during a quench,
showing that:
• Inductance is not the one measured at low ramp rate
• Inductance is lower than expected
• IFCC model can describe the inductance behavior
• Resistance measurement is possible only using reduced inductance
(measured, or even simulated). Using nominal inductance you get wrong.
 This method really affects protection studies, and gives more realistic and
accurate simulations.
Future steps:
 Implement the method with FEM (not average 𝜏, magnetic field…)
 Add inter-strand coupling currents
 New inductance measurements with more accurate signal analysis