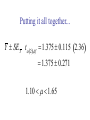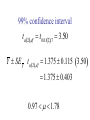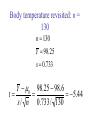Download ppt

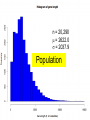
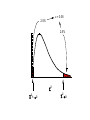
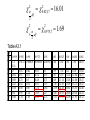
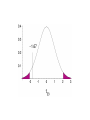
The Normal Distribution
QuickTime™ and a
TIFF (Uncompressed) decompressor
are needed to see this picture.
n = 20,290
 = 2622.0
 = 2037.9
Population
Y = 2675.4
s = 1539.2
Y = 2767.2
s = 2044.7
SAMPLES
Y = 2702.4
s = 1727.1
Y = 2588.8
s = 1620.5
Sampling distribution of the mean
Y = 2675.4
s = 1539.2
Y = 2702.4
s = 1727.1
Y = 2767.2
s = 2044.7
Y = 2588.8
s = 1620.5
Sampling distribution of the mean
1000 samples
Sampling distribution of the mean
Non-normal
Sampling distribution of the mean
Approximately normal
Sample means are normally
distributed
• The mean of the sample means is .
• The standard deviation of the sample means
is

Y 
n
*If the variable itself is normally distributed,
or sample size (n) is large
Standard error
The standard error of an estimate of a mean is
the standard deviation of the distribution of
sample means
Y 

n
s
We can approximate this by SE Y 
n

Distribution of means of samples
with n =10
Larger samples equal smaller
standard errors
Central limit theorem
The sum or mean of a large number of measurements
randomly sampled from any population is
approximately normally distributed.
Button pushing times
Frequency
Time (ms)
Distribution of means
Binomial Distribution
Normal approximation to the
binomial distribution
The bino mia l distrib utio n, w hen n umber o f trial s n is larg e
a nd p roba bility o f success p is no t clo se to 0 o r 1, i s
appr oxima ted b y a nor ma l d istribu tion ha ving mea n np
a nd sta ndard de viati on

np1 p .
Example
A scientist wants to determine if a loonie is a fair coin.
He carries out an experiment where he flips the coin
1,000,000 times, and counts the number of heads. Heads
come up 543,123 times. Using these data, test the fairness
of the loonie.
Inference about means
Because Y is normally distributed:


Z
Y 
Y
Y 

 n
But... We don’t know 
A good approximation to the standard normal is then:
Y
t
s/ n
Because we estimated s, t is not exactly
a standard normal!
t has a Student’s t distribution
Degrees of freedom
Degrees of freedom for the student’s t
distribution for a sample mean:
df = n - 1
Confidence interval for a mean
Y  2* SEY

Confidence interval for a mean
Y  SEY t 2, df
(2) = 2-tailed significance level

Df = degrees of freedom
SEY = standard error of the mean
95% confidence interval for a
mean
Example: Paradise flying snakes
QuickTime™ and a
TIFF (Uncompressed) decompressor
are needed to see this picture.
Undulation rates (in Hz)
0.9, 1.4, 1.2, 1.2, 1.3, 2.0, 1.4, 1.6
Estimate the mean and standard deviation
Y  1.375
s  0.324
n8

Find the standard error
Y  SE Y t 2,df
s
0.324
SE Y 

 0.115
n
8
Table A3.3
df
1
2
3
4
5
6
7
8
(1)
(1)
(1)
(1)
(1)
(1)
=0.1
=0.05
=0.025
=0.01
=0.005
=0.001
(2)=0.2 (2)=0.10 (2)=0.05 (2)=0.02 (2)=0.01 (2)=0.002
3.08
6.31
12.71
31.82
63.66
318.31
1.89
2.92
4.3
6.96
9.92
22.33
1.64
2.35
3.18
4.54
5.84
10.21
1.53
2.13
2.78
3.75
4.6
7.17
1.48
2.02
2.57
3.36
4.03
5.89
1.44
1.94
2.45
3.14
3.71
5.21
1.41
1.89
2.36
3.
3.5
4.79
1.4
1.86
2.31
2.9
3.36
4.5
Find the critical value of t
df  n 1  7
t 2,df  t 0.052,7  2.36
Putting it all together...
Y  SE Y t 2,df  1.375  0.115 2.36
 1.375  0.271
1.10    1.65
99% confidence interval
t2,df  t0.012,7  3.50
Y  SE Y t 2,df  1.375  0.115 3.50

 1.375  0.403
0.97    1.78
Confidence interval for the variance
df s

2
2

,df
2
 
2
df s
2 
2
1 ,df
2
 = 0.05
Frequency
2.5%
2.5%
2
2 1- /2
2 /2

2
2

2
,df


1 ,df
2
2
0.025,7

 16.01
2
0.975,7
 1.69
Table A3.1
df
X 0.999 0.995
1 1.6
3.9E-5
E-6
2 0
0.01
3 0.02 0.07
4 0.09 0.21
5 0.21 0.41
6 0.38 0.68
7 0.6
0.99
8 0.86 1.34

0.99
0.975
0.95
0.05
0.00016 0.00098 0.00393 3.84
0.025 0.01
5.02 6.63
0.005 0.001
7.88 10.83
0.02
0.11
0.3
0.55
0.87
1.24
1.65
7.38
9.35
11.14
12.83
14.45
16.01
17.53
10.6
12.84
14.86
16.75
18.55
20.28
21.95
0.05
0.22
0.48
0.83
1.24
1.69
2.18
0.1
0.35
0.71
1.15
1.64
2.17
2.73
5.99
7.81
9.49
11.07
12.59
14.07
15.51
9.21
11.34
13.28
15.09
16.81
18.48
20.09
13.82
16.27
18.47
20.52
22.46
24.32
26.12
95% confidence interval for the variance
of flying snake undulation rate
df s

2
2
2
 
2
,df
df s
2
2 
1 ,df
2
7 0.324
7 0.324 
2
 
16.01
1.69
2
2
0.0459    0.435
2
95% confidence interval for the standard
deviation of flying snake undulation rate
df s

2
2
2
 
,df
df s
2
2 
1 ,df
2
0.0459    0.435
0.21    0.66
One-sample t-test
The o ne-sa mpl e t-tes t com pare s the mea n of a rand om
samp le fr om a norma l p op ula tion with t he po pulat io n mean
pr opos ed in a null hy p othes is.
Hypotheses for one-sample t-tests
H0 : The mean of the population is 0.
HA: The mean of the population is not 0.
Test statistic for one-sample t-test
Y  0
t
s/ n
0 is the mean value proposed by H0

Example: Human body
temperature
H0 : Mean healthy human
body temperature is 98.6ºF
QuickTime™ and a
TIFF (Uncompressed) decompressor
are needed to see this picture.
HA: Mean healthy human
body temperature is not
98.6ºF
Human body temperature
n  24
Y  98.28
s  0.940
Y  0 98.28  98.6
t  

 1.67
s/ n
0.940 / 24
Degrees of freedom
df = n-1 = 23
Comparing t to its distribution to
find the P-value
A portion of the t table
df
...
20
21
22
23
24
25
(1)
(1)
(1)
(1)
(1)
=0.1
=0.05
=0.025
=0.01
=0.005
(2)=0.2 (2)=0.10 (2)=0.05 (2)=0.02 (2)=0.01
...
...
...
...
...
1.33
1.72
2.09
2.53
2.85
1.32
1.72
2.08
2.52
2.83
1.32
1.72
2.07
2.51
2.82
1.32
1.71
2.07
2.5
2.81
1.32
1.71
2.06
2.49
2.8
1.32
1.71
2.06
2.49
2.79
-1.67 is closer to 0 than -2.07,
so P > 
With these data, we cannot
reject the null hypothesis that
the mean human body
temperature is 98.6.
Body temperature revisited: n =
130
n  130
Y  98.25
s  0.733
Y  0 98.25  98.6
t  

 5.44
s / n 0.733/ 130
Body temperature revisited: n =
130
t  5.44
t0.05(2),129  1.98

is further out in the tail than the critical value, so we
t
could reject the null hypothesis. Human body
temperature is not 98.6ºF.

One-sample t-test: Assumptions
• The variable is normally distributed.
• The sample is a random sample.