* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Space and Shape Unit
Euclidean geometry wikipedia , lookup
Tensor operator wikipedia , lookup
Cartesian coordinate system wikipedia , lookup
Rotation formalisms in three dimensions wikipedia , lookup
Rotation matrix wikipedia , lookup
Rotations in 4-dimensional Euclidean space wikipedia , lookup
Euler angles wikipedia , lookup
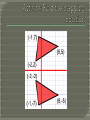
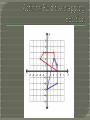
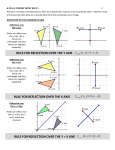
Geometry Grade 9 Math E1 Interpret, represent and apply mapping notation for transformations on the coordinate plane Reflected shapes have opposite orientation (cw and ccw) Line segments __________are bisected by the line of reflection For every rotation, there is a point of rotation (what the shape turns around) It does not change the orientation within the shape Unless the point of rotation in within the shape The lines between matching angles and the point of rotation are equal in a rotation The angle between matching sides and the point of rotation are all equal H I G J K B L Orientation of the shape does not change The sides must be proportional For the next 4 slides, try to create the mapping rule based on the different transformations First, record the pre-image and image coordinates Compare them in a table to look for a pattern Attempt the mapping rule In a reflection across the x-axis, values of x stay the same, values of y become negative y In a reflection across the y-axis, values of y stay the same, values of x become negative x At a 90 rotation: x and y values will interchange depending on the direction of the rotation, x or y will become negative At 180 rotation: values are maintained but become negative The image is an amplification, so the numbers are amplified as well Seen as a coefficient to x and y