* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Variables In Real Life: A Jar Of Spare Change
Analytic–synthetic distinction wikipedia , lookup
Intuitionistic logic wikipedia , lookup
Law of thought wikipedia , lookup
Propositional calculus wikipedia , lookup
Modal logic wikipedia , lookup
Interpretation (logic) wikipedia , lookup
Natural deduction wikipedia , lookup
Laws of Form wikipedia , lookup
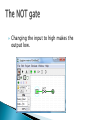
Professor James T. Williams, Jr. HONP112 Week 2 Lesson George Boole developed the mathematics that made modern computing possible, almost a century before the first computers were actually developed. A special kind of mathematics where there are only 2 possible values. These values are true and false. Special operators are used with these values to create expressions. A boolean expression will evaluate to either true or false in its entirety. There are three Boolean operators: AND OR NOT First, any expression in parenthesis Then the AND Then the OR The AND operator is a BINARY operator (i.e. it acts on two variables or expressions – “binary” in this context does not mean “base-2”) Example expression: A AND B Also can be written as A * B The resulting value of the expression depends on the values of A and B. An AND expression only evaluates to true if BOTH of the sub-expressions also evaluate to true. Otherwise, it evaluates to false. false AND false = false false AND true = false true AND false = false true AND true = true We can look at all the possibilities for the value of A*B as a truth table: A B A*B false false false false true false true false false true true true Assume: A is true and B is false What does the expression A * B evaluate to? What if A is true and B is true? Assume: A is true, B is false, C is true, D is true What does the expression A * B evaluate to? What does the expression C * D evaluate to? What does (A*B) * (C*D) evaluate to? The OR operator is a BINARY operator (i.e. it acts on two variables or expressions) Example expression: A OR B Also can be written as A + B (Careful – the plus sign does not mean “and”!!) The resulting value of the expression depends on the values of A and B. An OR expression only evaluates to true if EITHER of the sub-expressions also evaluate to true. Otherwise, it evaluates to false. false OR false = false false OR true = true true OR false = true true OR true = true We can look at all the possibilities for the value of A+B as a truth table: A B A+B false false false false true true true false true true true true Assume: A is true and B is false What does the expression A + B evaluate to? What if A is true and B is true? What if A is false and B is false? Assume: A is true, B is false, C is true, D is true What does the expression A + B evaluate to? What does the expression C + D evaluate to? What does (A+B) + (C+D) evaluate to? The NOT operator is a UNARY operator (i.e. it acts on one variable or expressions) Example expression: NOT A Also can be written as -A The resulting value of the expression depends on the value of A An NOT expression simply evaluates to the inverse value of the expression. NOT false = true NOT true = false We can look at all the possibilities for the value of -A as a truth table: A -A false true true false Assume: A is true and B is false What does the expression -A evaluate to? What does the expression -B evaluate to? Consider (B AND NOT A) OR (NOT D OR C). Assume A=1, B=1, C=1, and D=0 Put in the variable values and simplify as below: (1 AND NOT 1) OR (NOT 0 OR 1) (1 AND 0) OR (1 OR 1) 0 OR 1 1 Some more examples to work out in class or on your own time. Remember the order of operations. Assume A=1, B=1, C=1, and D=0 A OR D AND B = x (NOT B AND C) AND (A OR C) = x (B AND NOT D OR C) OR (NOT B AND B) = x (A AND B AND C) OR (B AND D) = x (A*B*C) + (B*D) = x [alt. version of above] All computer/digital circuits are constructed from various combinations of Boolean expressions. These are implemented in the computer by very tiny electronic components, built into chips, called “gates.” Depending on the values going into the gates, the end result will be either a logical 0 or 1. This corresponds with false or true. The gates in a computer understand the state 0 or 1 based on electrical voltage. Very generally speaking, for our purposes only, a 1 is about 5 volts, and a 0 is 0 volts or close to it. In real life these values may vary, but the idea is the same. It is more accurate to refer to the 1 and 0 in computer circuits as “high” or “low”. In case you wonder where the following screen shots are coming from... There is a free logic circuit simulator called Logisim. http://ozark.hendrix.edu/~burch/logisim/ Dark green is low, bright green is high Let’s see what happens with our logic gates. The AND gate is represented using the symbol below. It takes two inputs and produces a single output. For the output to be high, both inputs must be high. Let’s change one of the inputs to high. Because both are not high, the output is still low. Now let’s make both inputs high. Notice that now the output is high. The OR gate is represented using the symbol below. It takes two inputs and produces a single output. For the output to be high, only one of the inputs must be high. Let’s change one of the inputs to high. Notice that the output went high just by making one of the inputs high. The symbol below represents the NOT gate. This is also called an “inverter.” Notice that the output is high when the input is low. Changing the input to high makes the output low. (A AND NOT B) OR (C OR D) = x What is x? It depends on the values assigned to A, B, C, and D. Remember the values can only be true or false. (A AND NOT B) OR (C OR D) = x Assume A=true, B=false, C = false, D=true. (A AND NOT B) OR (C OR D) = x Assume A=false, B=false, C = false, D=true. (A AND NOT B) OR (C OR D) = x Assume A=false, B=true, C = false, D=false. Maybe in class, or on your own time … try to visualize them as circuits this time around. (A AND NOT B) AND (C OR D) (A * -B) * (C + D) [alt. version of above] (D + -B + C) * C -A * B * (C + A) Substitute different values for the variables. Try some with more or less variables. Experiment. Learn by doing. In circuit design, there are some special gates that are commonly used. The purpose of these gates is to make circuits simpler to build (less hardware = less effort = less cost). The gates we will discuss are not standard boolean operators, but are actually single circuits constructed from the standard boolean gates. NAND: “Not And” (AND gate followed by a NOT gate) NOR: “Not Or” (OR gate followed by a NOT gate) XOR: “Exclusive OR” (means that you only get a high output if EITHER of the inputs is high, not both. The circuit for XOR is more complex than for NAND or NOR) Same as AND followed by a NOT. Notice that we only draw the bubble part of the NOT gate on a NAND symbol (short-cut) Same as OR followed by a NOT. Notice that we only draw the bubble part of the NOT gate on a NOR symbol (short-cut) This means that only one of the two inputs can be high to get a high output. Notice how XOR symbols are drawn, and see the two simulations below. (The XOR circuit itself is not shown). Remember our earlier AND truth table. Just invert the output values and that is the NAND truth table. Let’s use 1 and 0 to represent true/high and false/low. A B A NAND B 0 0 1 0 1 1 1 0 1 1 1 0 Remember our earlier OR truth table. Just invert the output values and that is the NOR truth table. Let’s use 1 and 0 to represent true/high and false/low. A B A NOR B 0 0 1 0 1 0 1 0 0 1 1 0 Remember our earlier OR truth table. XOR is the same except that we get low when both inputs are high. Let’s use 1 and 0 to represent true/high and false/low. A B A XOR B 0 0 0 0 1 1 1 0 1 1 1 0 Know the truth tables for the six gates we have discussed. Know the various ways to represent the logical values of true/false. Be able to evaluate a boolean expression using the three simple operators. Be able to evaluate a circuit using any of the six logic gates. At this point, trying to imagine what the computer can do with these types of circuits may be a bit abstract. So let’s look at a concrete example of a real circuit that is used by every computer. You will not have to memorize this circuit but hopefully it will help illustrate a reallife application of a boolean logic circuit. This circuit (a “full adder”) is used by computers to add one column of two whole numbers (in base-2 of course). Again … You do not have to memorize this circuit, but just try to understand what it does. Imagine you are adding a single column of numbers. Notice there are three inputs. These are the first addend, the second addend, and the current value of the carry. There are two outputs. One is the result value that gets placed in the result column, and the other is the new carry value. We already know the addition algorithm … so let’s test the circuit to make sure it works correctly. Important: in the following slides, the “+” symbol will mean “plus” ! Assume the carry is 0, the first addend is 1, the second addend is 0. 0+1+0 = 1. 1 is not >= the base, so we set the result to 1, and the carry stays zero. Now, assume the carry is 0, the first addend is 1, the second addend is also 1. 0+1+1= 2. 2 is >= the base, so we subtract the base from the result, and set the carry to 1. OK, now assume that the carry, the first addend, and the second addend are all 1. 1+1+1 = 3. 3 is >= the base, so we subtract the base from the result, and set the carry to 1. A Question: By now you should be asking yourself “what if the two numbers we are adding are more than one column wide”? How does the adder handle multiple columns?? The answer: A whole bunch of individual full adders are “chained” together to account for many columns. When you move to the next column, the next full adder circuit takes in the two new addends, and also the carry value calculated from the previous column. The adder is just one example of a logic circuit that is really used inside a computer. There are numerous and varied logic circuits that make up an entire computer. Though we will not be examining the specific circuits, just keep the concept in mind as we continue our studies. I hope this lecture has provided insight into how boolean logic is related to computers. Our next lesson will expand on the boolean logic idea and how it applies to sets.