Download Variables In Real Life: A Jar Of Spare Change

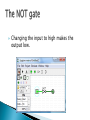
Professor James T. Williams, Jr.
HONP112
Week 2 Lesson

George Boole
developed the
mathematics that
made modern
computing
possible, almost a
century before the
first computers
were actually
developed.




A special kind of mathematics where there
are only 2 possible values.
These values are true and false.
Special operators are used with these values
to create expressions.
A boolean expression will evaluate to either
true or false in its entirety.




There are three Boolean operators:
AND
OR
NOT



First, any expression in parenthesis
Then the AND
Then the OR




The AND operator is a BINARY operator
(i.e. it acts on two variables or expressions
– “binary” in this context does not mean
“base-2”)
Example expression: A AND B
Also can be written as A * B
The resulting value of the expression
depends on the values of A and B.





An AND expression only evaluates to true if
BOTH of the sub-expressions also evaluate to
true. Otherwise, it evaluates to false.
false AND false = false
false AND true = false
true AND false = false
true AND true = true

We can look at all
the possibilities
for the value of
A*B as a truth
table:
A
B
A*B
false
false
false
false
true
false
true
false
false
true
true
true



Assume: A is true and B is false
What does the expression A * B evaluate to?
What if A is true and B is true?




Assume: A is true, B is false, C is true, D is
true
What does the expression A * B evaluate to?
What does the expression C * D evaluate to?
What does (A*B) * (C*D) evaluate to?




The OR operator is a BINARY operator (i.e. it
acts on two variables or expressions)
Example expression: A OR B
Also can be written as A + B (Careful – the
plus sign does not mean “and”!!)
The resulting value of the expression
depends on the values of A and B.





An OR expression only evaluates to true if
EITHER of the sub-expressions also evaluate
to true. Otherwise, it evaluates to false.
false OR false = false
false OR true = true
true OR false = true
true OR true = true

We can look at all
the possibilities
for the value of
A+B as a truth
table:
A
B
A+B
false
false
false
false
true
true
true
false
true
true
true
true




Assume: A is true and B is false
What does the expression A + B evaluate to?
What if A is true and B is true?
What if A is false and B is false?




Assume: A is true, B is false, C is true, D is
true
What does the expression A + B evaluate to?
What does the expression C + D evaluate to?
What does (A+B) + (C+D) evaluate to?




The NOT operator is a UNARY operator (i.e. it
acts on one variable or expressions)
Example expression: NOT A
Also can be written as -A
The resulting value of the expression
depends on the value of A



An NOT expression simply evaluates to the
inverse value of the expression.
NOT false = true
NOT true = false

We can look at all
the possibilities
for the value of -A
as a truth table:
A
-A
false
true
true
false



Assume: A is true and B is false
What does the expression -A evaluate to?
What does the expression -B evaluate to?







Consider (B AND NOT A) OR (NOT D OR C).
Assume A=1, B=1, C=1, and D=0
Put in the variable values and simplify as
below:
(1 AND NOT 1) OR (NOT 0 OR 1)
(1 AND 0) OR (1 OR 1)
0 OR 1
1







Some more examples to work out in class or
on your own time. Remember the order of
operations.
Assume A=1, B=1, C=1, and D=0
A OR D AND B = x
(NOT B AND C) AND (A OR C) = x
(B AND NOT D OR C) OR (NOT B AND B) = x
(A AND B AND C) OR (B AND D) = x
(A*B*C) + (B*D) = x [alt. version of above]



All computer/digital circuits are
constructed from various combinations of
Boolean expressions.
These are implemented in the computer by
very tiny electronic components, built into
chips, called “gates.”
Depending on the values going into the
gates, the end result will be either a logical
0 or 1. This corresponds with false or
true.




The gates in a computer understand the
state 0 or 1 based on electrical voltage.
Very generally speaking, for our purposes
only, a 1 is about 5 volts, and a 0 is 0 volts
or close to it.
In real life these values may vary, but the
idea is the same.
It is more accurate to refer to the 1 and 0
in computer circuits as “high” or “low”.





In case you wonder where the following
screen shots are coming from...
There is a free logic circuit simulator called
Logisim.
http://ozark.hendrix.edu/~burch/logisim/
Dark green is low, bright green is high
Let’s see what happens with our logic
gates.


The AND gate is represented using the
symbol below.
It takes two inputs and produces a single
output. For the output to be high, both
inputs must be high.


Let’s change one of the inputs to high.
Because both are not high, the output is
still low.


Now let’s make both inputs high.
Notice that now the output is high.


The OR gate is represented using the
symbol below.
It takes two inputs and produces a single
output. For the output to be high, only
one of the inputs must be high.


Let’s change one of the inputs to high.
Notice that the output went high just by
making one of the inputs high.


The symbol below represents the NOT gate.
This is also called an “inverter.”
Notice that the output is high when the input
is low.

Changing the input to high makes the
output low.



(A AND NOT B) OR (C OR D) = x
What is x? It depends on the values
assigned to A, B, C, and D.
Remember the values can only be true or
false.


(A AND NOT B) OR (C OR D) = x
Assume A=true, B=false, C = false,
D=true.


(A AND NOT B) OR (C OR D) = x
Assume A=false, B=false, C = false, D=true.


(A AND NOT B) OR (C OR D) = x
Assume A=false, B=true, C = false, D=false.







Maybe in class, or on your own time … try to
visualize them as circuits this time around.
(A AND NOT B) AND (C OR D)
(A * -B) * (C + D) [alt. version of above]
(D + -B + C) * C
-A * B * (C + A)
Substitute different values for the variables.
Try some with more or less variables.
Experiment. Learn by doing.



In circuit design, there are some special
gates that are commonly used.
The purpose of these gates is to make
circuits simpler to build (less hardware =
less effort = less cost).
The gates we will discuss are not standard
boolean operators, but are actually single
circuits constructed from the standard
boolean gates.



NAND: “Not And” (AND gate followed by a
NOT gate)
NOR: “Not Or” (OR gate followed by a NOT
gate)
XOR: “Exclusive OR” (means that you only
get a high output if EITHER of the inputs is
high, not both. The circuit for XOR is more
complex than for NAND or NOR)

Same as AND followed by a NOT. Notice
that we only draw the bubble part of the
NOT gate on a NAND symbol (short-cut)

Same as OR followed by a NOT. Notice
that we only draw the bubble part of the
NOT gate on a NOR symbol (short-cut)

This means that only one of the two inputs
can be high to get a high output. Notice
how XOR symbols are drawn, and see the
two simulations below. (The XOR circuit
itself is not shown).


Remember our
earlier AND truth
table. Just invert
the output values
and that is the
NAND truth table.
Let’s use 1 and 0
to represent
true/high and
false/low.
A
B
A NAND B
0
0
1
0
1
1
1
0
1
1
1
0


Remember our
earlier OR truth
table. Just invert
the output values
and that is the
NOR truth table.
Let’s use 1 and 0
to represent
true/high and
false/low.
A
B
A NOR B
0
0
1
0
1
0
1
0
0
1
1
0


Remember our
earlier OR truth
table. XOR is the
same except that
we get low when
both inputs are
high.
Let’s use 1 and 0 to
represent true/high
and false/low.
A
B
A XOR B
0
0
0
0
1
1
1
0
1
1
1
0




Know the truth tables for the six gates we
have discussed.
Know the various ways to represent the
logical values of true/false.
Be able to evaluate a boolean expression
using the three simple operators.
Be able to evaluate a circuit using any of
the six logic gates.



At this point, trying to imagine what the
computer can do with these types of
circuits may be a bit abstract.
So let’s look at a concrete example of a
real circuit that is used by every computer.
You will not have to memorize this circuit
but hopefully it will help illustrate a reallife application of a boolean logic circuit.


This circuit (a “full adder”) is used by computers to add one
column of two whole numbers (in base-2 of course).
Again … You do not have to memorize this circuit, but just
try to understand what it does.





Imagine you are adding a single column of numbers.
Notice there are three inputs. These are the first
addend, the second addend, and the current value of
the carry.
There are two outputs. One is the result value that
gets placed in the result column, and the other is the
new carry value.
We already know the addition algorithm … so let’s test
the circuit to make sure it works correctly.
Important: in the following slides, the “+” symbol will
mean “plus” !


Assume the carry is 0, the first addend is 1, the second
addend is 0.
0+1+0 = 1. 1 is not >= the base, so we set the result to 1,
and the carry stays zero.


Now, assume the carry is 0, the first addend is 1, the
second addend is also 1.
0+1+1= 2. 2 is >= the base, so we subtract the base from
the result, and set the carry to 1.


OK, now assume that the carry, the first addend, and the
second addend are all 1.
1+1+1 = 3. 3 is >= the base, so we subtract the base
from the result, and set the carry to 1.


A Question: By now you should be asking yourself
“what if the two numbers we are adding are more
than one column wide”? How does the adder
handle multiple columns??
The answer: A whole bunch of individual full
adders are “chained” together to account for
many columns. When you move to the next
column, the next full adder circuit takes in the
two new addends, and also the carry value
calculated from the previous column.




The adder is just one example of a logic circuit
that is really used inside a computer. There are
numerous and varied logic circuits that make up
an entire computer.
Though we will not be examining the specific
circuits, just keep the concept in mind as we
continue our studies.
I hope this lecture has provided insight into how
boolean logic is related to computers.
Our next lesson will expand on the boolean logic
idea and how it applies to sets.