* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Multiplying Polynomials Using Algebra Tiles
Polynomial ring wikipedia , lookup
Factorization wikipedia , lookup
Polynomial greatest common divisor wikipedia , lookup
Factorization of polynomials over finite fields wikipedia , lookup
Linear algebra wikipedia , lookup
Fundamental theorem of algebra wikipedia , lookup
Boolean algebras canonically defined wikipedia , lookup
Complexification (Lie group) wikipedia , lookup
Heyting algebra wikipedia , lookup
Universal enveloping algebra wikipedia , lookup
Geometric algebra wikipedia , lookup
Exterior algebra wikipedia , lookup
Laws of Form wikipedia , lookup
Homological algebra wikipedia , lookup
Vertex operator algebra wikipedia , lookup
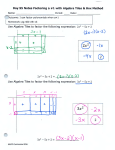
MULTIPLYING POLYNOMIALS USING ALGEBRA TILES SOL A.2b REVIEW Represent Polynomials Using Algebra Tiles 1) Represent x2 + 3 2) Represent x2 + 4x – 2 REVIEW Represent Polynomials Using Algebra Tiles 3) Represent 3x2 – x 4) Represent 2x2 + x - 3 Multiplying Polynomials Using Algebra Tiles 1) Multiply x(x + 3) using Algebra tiles 1) Measure side lengths of (x) and (x + 3) since x and x + 3 are the two factors Length of x Length of 3 Length of x Multiplying Polynomials Using Algebra Tiles 1) Multiply x(x + 3) using Algebra tiles x 2) Draw lines to complete the rectangle and each part in the rectangle. x+3 Multiplying Polynomials Using Algebra Tiles 1) Multiply x(x + 3) using Algebra tiles x 3) Fill in the spaces with the correct Algebra tiles. x+3 Therefore, x(x + 3) = x2 + 3x Multiplying Polynomials ■ Use the distributive property to check your answer. 2 x ■ x(x + 3) = + 3x Multiplying Binomials Using Algebra Tiles 2) Multiply (x + 2)(x + 4) using Algebra tiles Length of x + 4 1) Measure side lengths of (x + 2) and (x + 4) since x + 2 and x + 4 are the two factors Length of x+2 Multiplying Polynomials Using Algebra Tiles 2) Multiply (x + 2)(x + 4) using Algebra tiles x+4 2) Draw lines to complete the rectangle and each part in the rectangle. x+2 Multiplying Polynomials Using Algebra Tiles 2) Multiply (x + 2)(x + 4) using Algebra tiles x+4 3) Fill in the spaces with the correct Algebra tiles. x+2 Therefore, (x + 2)(x + 4) = x2 + 6x + 8 Multiplying Binomials Using Algebra Tiles 3) Multiply (2x + 1)(x + 2) using Algebra tiles Length of 2x + 1 1) Measure side lengths of (2x + 1) and (x + 2) since 2x + 1 and x + 2 are the two factors Length of x+2 Multiplying Polynomials Using Algebra Tiles 2) Multiply (2x + 1)(x + 2) using Algebra tiles 2x + 1 2) Draw lines to complete the rectangle and each part in the rectangle. x+2 Multiplying Polynomials Using Algebra Tiles 2) Multiply (2x + 1)(x + 2) using Algebra tiles 2x + 1 3) Fill in the spaces with the correct Algebra tiles. x+2 Therefore, (2x + 1)(x + 2) = 2x2 + 5x + 2 Multiplying Binomials ■ 4) Multiply (x + 2)(x + 3) using Algebra Tiles x+2 x+3 Mark the correct length on the sides Draw lines to complete the rectangle. Fill in the rectangle with the correct Algebra tiles. Therefore, (x + 2)(x + 3) = x2 + 5x + 6