Download Chemical Kinetics - mvhs

Brown, LeMay, Ch 14
AP Chemistry
Monta Vista High School
1
14.0: Chemical kinetics

Study of the rates of reactions
Reaction rate is affected by:
1. Concentration of reactants
2. Temperature of the reaction
3. Presence/absence of a catalyst
4. Surface area of solid or liquid reactants
and/or catalysts
Rates of Reaction animation
2
14.1: Reaction rate
 A measure of the (average) speed of a reaction
 Expressed as rate of appearance (+,
production) or disappearance (-, reaction)
 mol 


mol
M [ ] = concentration,
L


Rate 
or 

usually M
t
t
t
 Related to stoichiometry of reaction
aA + bB → cC
1 [C ]
1 [ A]
1 [ B ]
Rate  


c t
a t
b t
3
14.1: Reaction rates
Ex: Balance the following reaction, then
determine how the rates of each compound
are related:
2 N2O5 (g) → 4 NO2 (g) + O2 (g)
[O2 ] 1 [ NO2 ]
1 [ N 2O5 ]
Rate 

t
4 t
2
t
• If [O2]/t = 5.0 M/s, what is [N2O5]/t?
5.0 M O 2 2 mol N 2 O5 (consumed)

 10. M/s N 2 O5
s
1 mol O 2
4
Reaction Rates
 Average Rate: Rate of a reaction over a given period of
time. Since the rates of reactions vary with time, this
rate only gives an average over a period of time. It can
be calculated by calculating change in concentration
with time.
 Instantaneous Rate: Rate of reaction at ONE given
point of time. It can be calculated from conc.- time
graph by finding the tangent of the graph.
 Initial Rate: Rate of reaction at t=0. (its
instantaneous rate at t=0). It is used in rate law
equation and to study most reactions. Since most
reactions are reversible, to find rate of reaction, both
forward and reverse rates should be taken into
account, which can be complicated. By using initial
rate that problem does not exist.
5
14.2: Rate & concentration
 Rate law: shows how the rate of reaction depends on
the concentration of reactant(s).
aA + bB → cC
Rate = k[A]m[B]n
Ex: NH4+ (aq) + NO21- (aq) → N2 (g) + 2 H2O (l)
The rate law may be:
Rate = k [NH4+]1 [NO21-]2
or
Rate = k [NH4+]1/2 [NO21-]3
 The rate law can only be determined based
on experimental evidence; it cannot be
predicted by the overall balanced reaction!
6
Finding Rate Law Using Initial Rates
 This method is used to determine the rate
law for various reactions. In this method,
initial rate of a reaction is measured at
various reactant concentrations and the data
is recorded.
 The data for initial rates method looks like
the example given on the next slide.
7
 Ex: Determining the rate law using the following data:
Exp #
[NH4+]
[NO21-]
Initial rate (M/s)
1
2
3
x3
0.50
0.50
1.5
x1
x1
0.20
0.40
0.40
x2
x9
3.0 x 10-3 x 2
6.0 x 10-3
54 x 10-3
Rate = k [NH4+]m [NO2-]n
3m = rate = 9, m = 2
2n = rate = 2 , n = 1
Rate = k [NH4+]2 [NO2-]1
3.0 x 10-3 = k [0.50]2 [0.20]1
k = 0.060
Rate = 0.060 [NH4+]2 [NO2-]1
8


Rate Exp 1 3.0 x103 k[ NH 4 ]m [ NO2 ]n k[0.50]m [0.20]n



 m
 n
3
Rate Exp 2 6.0 x10
k[0.50]m [0.40]n
k[ NH 4 ] [ NO2 ]
3.0 x103 k[0.50]m [0.20]n

3
6.0 x10
k[0.50]m [0.40]n
n
1 1
   ,n 1
2 2
Rate Exp 1 3.0 x103 k[0.50]m [0.20]1


3
Rate Exp 3 54 x10
k[1.5]m [0.40]1
m
1 1 1
    , m  2
18  3   2 
Rate = k [NH4+]2 [NO2-]1
9
Practice Problem:
2 A + 2 B C + D
The following data about the reaction above were obtained
from three experiments:
(a) What is the rate equation for the reaction?
(b) What is the numerical value of the rate constant k? What
are its dimensions?
(c)Propose a reaction mechanism for this reaction.
Experiment
1
2
3
[A]
[B]
0.60 0.15
0.20 0.60
0.20 0.15
Initial Rate of Formation of
C in M
6.3´10-3
2.8´10-3
7.0´10-4
10
(a)rate = k [A]2[B]1
(b)
rate
6.3  10
k
[A]2 [B]

3
mol  L-1  min -1
0.60 mol  L  (0.15 mol  L )
-1 2
-1
= 0.12 L2mol-2min-1
(c) A + A ® A2 (fast)
A2 + B ® C + Q (slow)
Q + B ® D (fast)
11
AP test 2010 form B question
12
Determining Rate Law by Determining the
Change in Concentration of reactants over
time: Integration Method
 In this method, the change in concentration of
reactants is studied over time. This data can
give rate law either graphically or by
calculations.
 Integration of rate law equations give
integrated rate law equations, which can be
used to calculate the concentration of a
reactant [A]t at time t.
13
14.3 Change of concentration over time
 Order: the “level” or “degree” of a rate
 Reaction order: the exponents in a rate law
 Usually whole numbers, but can be fractions or
negative (think inhibitors)
Ex: NH4+ (aq) + NO21- (aq) → N2 (g) + 2 H2O
(l)
If:
Rate = k [NH4+]2 [NO21-]1
Then:
 A “2nd order” reaction with respect to [NH4+]
 1st order with respect to [NO21-]
 3rd order overall (2 + 1 = 3)
14
Figure 1: Comparison of reaction orders based on the generic
reaction: A → C.
Rxn
Rate law
order (simple format)
A
Rate  
t
Rate  k[ A]0
Zero
order
Rate = k
Rate law
(relating [A] to [A0])
 A t
d A

k
dt
d A  -kdt
t
d A  -k  dt

 
A
0
Units of rate
constant (k)
[A]t = -kt + [A0]
(M) = -(k)(s) + (M)
therefore
(k)(s) = (M)
0
so
At  A0  -k (t  0) (k) = M/s
or
[A]t = -kt + [A](k)
0 = mol·L-1·s-1
[A]t
Time
15
Rxn
Rate law
order (simple format)
A
Rate  
t
Rate  k[ A]
1
1st
order
Rate law
(relating [A] to [A0])
Units of rate
constant (k)
d A
 -kdt
A
ln[A]t = -kt +
ln[A0]
__ = -(k)(s) +
__
d  A

 k  A
dt
 A t

 
d  A
 -k  dt
A
0
t
therefore
ln At  ln A0  -k (t  0) (k)(s) = __
A
0
ln[A]t = -kt + ln[A]0
[A]t
log[A]t = -kt / 2.303 + log[A]0
Time
ln [A]t
Time
so
(k) = 1/s
or
(k) = s-1
16
A
Rate  
t
Rate  k[ A]2
(or  k[ A][ B])
d A
2

 k A
dt
 A t

 
[A]t
Time
d  A
 -k  dt
2
A
0
t
therefore
1  1 
  -k (t  0) (k)(s) = (1/M)

  
A t  A 0 
so
1
1
(k) = 1/(M•s)
 kt 
[ A]t
[ A]0
or
(k) = mol-1·L·s-1
A
2nd
order
d A
 -kdt
2
A
1/[A]t = kt + 1/[A0]
(1/M) =
(k)(s)+(1/M)
0
1 / [A]t
(k) = M-1·s-1
Time
17
 “We can simplify the treatment somewhat by recognizing that, as the reaction
proceeds, the loss of reactants (and the increase in product)
will be
nd order,
*If
Rate
=
k
[A][B];
referred
to
as
“2
Class
stoichiometrically linked. Setting the loss of reactants (or appearance
of
product) = x, we get
II”
 We re-arrange to group like terms
 The integration of this equation is not trivial, but we can look it up in
integration tables, and find a solution. On substitution back for x, we get:
 Note that the integrated rate equation shows that a plot of ln [A]/[B] vs. time
will give a straight line for a 2nd-order, Class II reaction. Note also that the
treatment fails if the initial concentrations of the two substrates are the same,
i.e. the logarithmic term becomes zero. In this case, the reaction can be treated
by the same formalism as for Class I reactions, or alternatively, the initial
concentrations can be handle if the values are very slightly different.”
(Source: http://www.life.uiuc.edu/crofts/bioph354/lect18_sup.html)
18
 Other methods to determine the units of k:
 Memorize this:
1 overall order
Ex: 2nd order:
M
(k) 
time unit
1 2
M
(k) 
s
M -1
-1
1
(k) 
 M s
s
 Solve the rate law for units:
Rate  k[A]3[B]
M


3
4

(
k)(M)
(M)

(
k)(M)


 time unit 
 1 
3
1
(k)   3   M  s
 M s 
19
Radioactive decay: a first order reaction
 Half-life (t½): time for ½ a radioactive (i.e., having an
unstable p/n ratio) material to decay (form 2 or more
stable atoms)
d A
Rate  
 -kt12
A
2
ln 1  ln 2  -kt
 ln 2  -kt
1
1
1
2
2
ln 2 0.693
k

t1/2
t1/2
20
http://www.chm.davidson.edu/vce/kinetics/i
ntegratedratelaws.html (interactive on integrated
rate laws)
Practice Problem: 1998 b,c
21
14.4: Temperature & rate

Increasing T increases reaction rate
The Collision Model:
1. Molecules must collide in order to react.
2. Not every collision results in a reaction.
(Ex: at room T, in a mixture of H2 and I2,
1010 collisions occur each sec; however, only
1 in every 1013 collisions results in a reaction
between H2 and I2.) Molecules must
collide in the correct orientation.
22
 Activation energy ( Ea ): minimum energy required to
initiate a chemical reaction
Activated complex
Reactants
Energy
Ea
Erxn
Products
Rxn pathway (or rxn coordinate)
Note that:
Erxn, forward = - Erxn, backward
Ea, forward ≠ Ea, backward
23
Figure 2: Change in Potential
Energy Reaction and collision animation
 Reaction and collision
animation Reaction
and collision
animation Reaction
and collision
animation
24
Arrhenius equation: Relationship
between rate and T
kAe
-E a / RT
A = frequency factor (related to # of
collisions)
R = 8.314 J/(mol•K)
- Ea
ln k 
 ln A
RT
Svante Arrhenius
(1859-1927)
25
 How to determine Ea: perform rate
experiments using various T (and keep
concentrations constant.)
 Ea 1
ln k 
 ln A
ln A
R T
 Ea
Slope 
R
ln k
k
Temp
(K)
 Ea
ln k1 
 ln A
RT1
 Ea
ln k 2 
 ln A
RT2
1/T (K-1)
k1  Ea  1 1 
  
ln 
k2
R  T1 T2 
http://www.shodor.org/unchem/advanced/kin/arrhenius.html
26
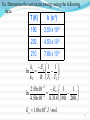
Ex: Determine the activation energy using the following
data:
T (K)
k (s-1)
190.
2.50 x 10-2
200.
4.50 x 10-2
210.
7.66 x 10-2
k1  Ea  1 1 
  
ln 
k2
R  T1 T2 
2.50 x102  Ea  1
1 
ln




2
4.50 x10
8.314  190. 200. 
Ea  1.86 x10 4 J / mol
27
Practice Problem:
The rate constant for the reaction
H2(g) + I2(g) ---> 2HI(g)
is 5.4 x 10-4 M-1s-1 at 326 oC. At 410 oC the rate constant
was found to be 2.8 x 10-2 M-1s-1.
Calculate the
a) activation energy
and
b) high temperature limiting rate constant
for this reaction.
28
We know the rate constant for the reaction at
two different temperatures and thus we can
calculate the activation energy from the above
relation. First, and always, convert all
temperatures to Kelvin, an absolute
temperature scale. Then simply solve for Ea in
units of R.
ln(5.4 x 10-4 M-1s -1/ 2.8 x 10-2 M-1s-1) = (-Ea /R
){1/599 K - 1/683 K}
-3.9484 = - Ea/R {2.053 x 10-4 K-1}
Ea= (1.923 x 104 K) (8.314 J/K mol)
Ea= 1.60 x 105 J/mol
29
Now that we know Ea, the pre-exponential factor,
A, (which is the largest rate constant that the
reaction can possibly have) can be evaluated from
any measure of the absolute rate constant of the
reaction.
so
5.4 x 10-4 M -1s-1 =
A exp{-(1.60 x 105 J/mol)/((8.314 J/K mol)(599K))}
(5.4 x 10-4 M-1s-1) / (1.141x10-14) = 4.73 x 1010 M-1s-1
The infinite temperature rate constant is 4.73 x
1010 M-1s-1
30
Good Resource for Kinetics Practice
Problems:
 http://highered.mcgraw-
hill.com/sites/0072396814/student_view0/chapter16/i
nteractive_quiz_2.html
31
14.5: Reaction Mechanisms
The actual process of atomic rearrangement through
which reactants become products.
Elementary steps (elementary processes): a single event
or step (reaction) in a multi-step reaction
Ex: O3 (g) → O2 (g) + O* (g)
 Always add to give the overall chemical equation
 Non-elementary: Ex: CH4 (g) + 2 O2 (g) → CO2 (g) + 2
H2O (g)
Molecularity:
 Number of molecules participating as reactants in an
elementary step
1 molecule = unimolecular
2 (in a simultaneous collision) = bimolecular
3 = termolecular
4 = not likely
32
14.5: Reaction Mechanisms
Rules for predicting a permissible mechanism:
1. The stoichiometry of the balanced reaction must be
followed.
2. The rate-determining step (RDS) is always the SLOW
elementary step of the reaction. The coefficients in the
SLOW elementary step and previous steps
determine the orders of reactants in the rate law.
3. Intermediates (chemicals produced in one step that
react in another) may be introduced as long as they are
used up at the end of the mechanism. They will also not
appear in the rate law.
4. The true rate law can only be determined
experimentally; it cannot be predicted by the balanced
reaction.
33
Figure 3: Example reaction: O2 + 2 NO + H2 → 2 HNO2
Rate-Determining Step
Proposed mechanism
Possibilities
Step 1: 1 O2 + 1 NO → NO3
SLOW
Step 2: NO + NO3 → N2O4
FAST
Step 3: H2 + N2O4 → 2 HNO2
FAST
If these steps represent the true mechanism, and
Step 1 is the SLOW step (RDS), then:
Rate = k [O2]1 [NO]1
34
Figure 3: Example reaction: O2 + 2 NO + H2 → 2 HNO2
Rate-Determining Step
Proposed mechanism
Possibility #2
Step 1: 1 O2 + 1 NO → NO3
FAST
Step 2: 1 NO + NO3 → N2O4
SLOW
Step 3: H2 + N2O4 → 2 HNO2
FAST
If these steps represent the true mechanism, and
Step 2 is the SLOW step (RDS), then:
Rate = k [O2]1 [NO]2
35
Figure 3: Example reaction: O2 + 2 NO + H2 → 2 HNO2
Rate-Determining Step
Proposed mechanism
Possibility #3
Step 1: 1 O2 + 1 NO → NO3
FAST
Step 2: 1 NO + NO3 → N2O4
FAST
Step 3: 1 H2 + N2O4 → 2 HNO2
SLOW
If these steps represent the true mechanism, and
Step 3 is the SLOW step (RDS), then:
Rate = k [O2]1 [NO]2 [H2]1
36
14.6: Catalysts
 Substance that changes the rate of a reaction
without undergoing a permanent chemical
change itself
 Generally, lowers the activation energy
 Typically works by adsorption, which
brings reactant molecules close to each
Ea,
other
uncatalyzed
Ea, catalyzed
Energy
Erxn
Rxn coordinate
37