Download Basic Concepts of Epidemic Models

Basic Concepts of Epidemic Models
Nikos Demiris
Stats Dept @ Athens University of Economics and Business
UCL Workshop on Infectious Disease Modelling in Public Health Policy:
Current status and challenges, 4th July 2016
1 / 33
Outline of this lecture
A bit of (local) Epidemic History
Epidemic Models: Motivation and Basic Concepts
Vaccination
Multitype Models: Why and How
Some results for Stochastic Epidemics (hopefully)
Contemporary Epidemic Models (perhaps)
2 / 33
One the fathers of Epidemiology is
3 / 33
Not this guy
4 / 33
But the great John Snow
Solved the Cholera
problem in Soho
5 / 33
Soho, 1854
Soho was not connected to
the London sewer system
By inspection of the map
Snow realised that the
Broad Street pump was the
focus of infection
He removed the handle and
the epidemic died out
6 / 33
A new theory
Went beyond the miasma
theory
’Bad air’ (= mala aria)
Important note: None of the
pub employees of the local
brewery was affected
Daily allowance of beer → they
did not consume water from
the nearby well.
Boiling water when brewing →
kills cholera bacteria
7 / 33
Why Epidemic Models
Understanding the mechanism of disease spread is important
for disease control (or eradication)
Epidemic Models are a natural tool for preparing (scenario
testing) for a forthcoming epidemic/pandemic, dealing with
an emerging disease or bioterrorism
Also, they provide the framework for control measures:
calculating the critical vaccination coverage and the optimal
vaccination policy
Evaluation of the cost-effectiveness of different interventions
8 / 33
The structure of Epidemic Models
They are mathematical models appropriate for describing the
transmission of an infectious disease in a population of
individuals such as humans, animals, computers, plants
They have also been used for describing the transmission of
rumours, financial crises, information...
Here we shall focus on person-to-person transmission.
Modifications are required for host-vector diseases and rumour
models.
9 / 33
Epidemic Models: Challenges
Strong dependencies are inherently present
The chance (hazard) that an individual gets infected depends
on the status of others in their vicinity.
Makes model analysis and statistical inference hard.
The epidemic process is never fully observed
Models are defined in terms of who infected whom and when
did this happen–although genetic info is changing that.
We typically only observe the times that symptoms appear.
Makes the statistical analysis non-trivial.
10 / 33
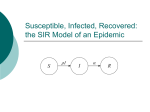
The deterministic General Epidemic (Kermack
and McKendrick 1927)
There are three possible states (compartments):
Susceptible
Infected
S→I→R
Removed
Individuals move between these states based on the following
system:
dS
= −λS(t)I (t)
dt
dI
= λS(t)I (t) − γI (t)
dt
dR
= γI (t)
dt
dI
dR
Note that dS
dt + dt + dt = 0 so that the population size is closed
(no demography), homogeneous and homogeneously mixing
11 / 33
Implications of this Model
Dividing the 1st and 3rd equations we get:
dS
dR
= −R0 S
R0 = λγ is a threshold parameter that largely determines the
system behaviour
Integrating gives: S(t) = S(0)e −R0 (R(t)−R(0))
For a large population and t → ∞ we have 1 − τ = e −τ R0 .
This transcendental equation has a non-trivial solution iff
R0 > 1, whence τ ↑ with R0 . Otherwise τ = 0
dI
Alternatively, I (t) is increasing ( dt
> 0) when R0 >
1
S(0)
Both suggest a threshold theorem: There will be a major
(minor) epidemic iff R0 > 1 (R0 < 1)
What is R0 ?
12 / 33
R0 values for some well-known diseases
Disease
Transmission
R0
Measles
Airborne
12-18
Pertussis
Airborne droplet
12-17
Diphtheria
Saliva
6-7
Smallpox
Social contact
5-7
Polio
Fecal-oral route
5-7
Rubella
Airborne droplet
5-7
Mumps
Airborne droplet
4-7
HIV/AIDS
Sexual contact
2-5
SARS
Airborne droplet
2-5
Influenza (1918 pandemic strain) Airborne droplet
2-3
13 / 33
Epidemic Control: Vaccination
Disease control is, perhaps, the most important practical
reason for using epidemic models
Suppose that a (perfect) vaccine is available and we are
interested in estimating the proportion, say ω, to be
immunised in order to avoid a large outbreak
The effective transmission rate is now λ(1 − ω) so
R0 (ω) = λ(1−ω)
= (1 − ω)R0
γ
We wish to achieve R0 (ω) < 1 or ω > ωc = 1 −
1
R0
We call ωc as the critical vaccination coverage, e.g.
ωc = {0.5, 0.8, 0.9} for R0 = {2, 5, 10} respectively.
The state where ω > ωc is referred to as herd immunity
14 / 33
Imperfect Vaccine
The above calculations were made assuming that a vaccine
offers perfect immunity.
Suppose that the vaccine is imperfect with efficacy ψ. Then
we have R0 (ω, ψ) = (1 − ω)R0 + ω(1 − ψ)R0 .
The condition R0 (ω, ψ) < 1 now gives ω(ψ) > ωc (ψ) =
So ψ < 1 −
1
R0
1− R1
0
ψ
implies that herd immunity is impossible!
Indeed, for a disease with R0 = 10 we need 90% coverage. Any
vaccine with ψ < 90% cannot achieve that aim, even if everyone is
vaccinated.
A crude R0 estimate can be obtained from τ = 1 − e −τ R0 so
)
R̂0 = − log(1−τ
, with τ the proportion infected in a historical
τ
outbreak
15 / 33
What else matters in Epidemic Transmission?
Realistic populations are not homogeneous, nor
homogeneously mixing.
Age is important, should we bother with age-grouping?
Yes! A trivial – fictitious illustration for non-statisticians:
Vaccine A
Efficacy
78% =
273
350
Vaccine B
83% =
289
350
16 / 33
Age does matter: confounding
Vaccine A
Vaccine B
Children
93% =
81
87
87% =
234
270
Adults
73% =
192
263
69% =
55
80
Efficacy
78% =
273
350
83% =
289
350
17 / 33
A solution: multitype models
Split the population into k age groups → k 2 contact rates
Can be over-parametrised. Marc’s talk will use Polymod data:
contact survey, gives a rough idea of how age classes mix
Disentangles the social and biological components of disease
transmission
R0 is now the largest eigenvalue of a matrix
Vaccination more involved but follows from the same
principles
18 / 33
Is everything changing with Big Data?
In 2009 a group from Google published in Nature a study
which used data from their Search Engine to predict/nowcast
ILI activity
A comparison of model estimates for the mid-Atlantic
region (black) against CDC-reported ILI percentages (red),
including points over which the model was fit and validated.
J Ginsberg et al. Nature 000, 1-3 (2008) doi:10.1038/nature07634
Can such methods/data replace the current (more expensive)
surveillance systems?
19 / 33
Not yet
In 2013 GFT massively overestimated the peak of Flu activity
But this was a fresh idea and can function to parametrise
some components of the epidemic process.
It represent a currently active research area.
20 / 33
Epidemic Models: Deterministic and
Stochastic
The former can be thought of as the ‘mean’ of the latter,
when appropriately defined (Kurtz, LLN and CLT)
Stochastic models are more natural since most relevant events
like the disease transmission or extinction are defined in terms
of their probability.
Deterministic models are simpler (but not simple!) to analyse
and dominated the previous century. Stochastic models are
increasingly popular as they appear in many high-impact
publications of this century.
Both types are useful.
21 / 33
Stochastic SIR Epidemic Models
The (Markov) stochastic version was introduced by Bartlett
(1949) and is known as the ‘general stochastic epidemic’.
Each individual, while infectious, makes contacts according to
the points of a Poisson process with intensity λ/N. The
Poisson contact processes are independent.
The infectious periods, say Ij , are i.i.d. Exp(γ). This is a
common (and often hidden) assumption in ODE models and
in Markov Processes.
We shall be concerned with the case where the Ij ’s are not
necessarily exponential (usually Gamma). This model has
been known as the generalised stochastic epidemic (GSE).
22 / 33
How does the model look?
Initially the model is very much like a (BGW) branching
process where
Birth → new infection
Death → removal
This can be made fully rigorous using a coupling argument
(Ball 1983) as follows:
The life span of ancestor j is Ij , Ij ’s independent.
Each ancestor gives birth during their lifetime at the points of
a Poisson process with rate λ/N.
Then, the two processes ‘agree’ until time C log(N) (Ball and
Donnelly 1995).
So we can use all the machinery of branching processes
(Jagers 1975) to derive results for the initial behaviour of
epidemics.
23 / 33
Branching Process Approximation
Let {Y (t); t ≥ 0} be the number of individuals alive at time t and
D the number of offspring of a given individual. If the initial
population size is m then there will be on average mE (D)ν
individuals in the ν-th generation
Clearly the process will become extinct iff E (D) ≤ 1
Using standard results from (Jagers 1975) one can show that
when E (D) > 1 there will be extinction w.p. q m and
explosion otherwise. q is the smallest solution of θ = E (θD ).
Summary: E (D) ≤ 1 → extinction w .p. 1
extinction w .p. q m
E (D) > 1 →
explosion w .p. 1 − q m
Note that given I = i the number of children D ∼ Po(λi)
Which (after some work) gives E (D) = λE (I ) = R0 !
Hence, E (D) ≤ 1 (E (D) > 1) → R0 ≤ 1 (→ R0 > 1)
24 / 33
Thresholds and Phase Transitions
We have seen that R0 determines whether or not an epidemic
can occur.
This dramatic change in the system behaviour has been
observed in many processes in nature (0 and 100 degrees
temperature, . . . ) and some connections will be given,
particularly with random graphs and percolation models.
Random graphs have also been used as population models.
Social (and other) networks are often described with random
graph models (p ∗ , powerlaw-type, . . . ).
The analysis of such systems is largely similar to the analysis
of stochastic epidemics, particularly the final outcome.
25 / 33
The final size distribution of the GSE
Let pk be the probability that k individuals are ultimately
infected, 0 ≤ k ≤ N. Then
n−k
l
X
n
l−k pk
, 0 ≤ l ≤ N,
h ik+m =
l
λ(n−l)
k=0 φ
n
where φ(θ) is the Laplace transform of I and m the number of
initial infectives.
This triangular system of equations was derived in Ball (1986)
using Laplace transforms and a Wald-type identity.
It is exact and, in principle, straightforward to solve
numerically.
In practice, however, numerical problems arise even for
moderate population sizes, say N = 50, due to the nature of
the solution.
The likelihood is analytically and numerically intractable:
26 / 33
The final size distribution of the GSE
27 / 33
A (complementary) solution: Asymptotics
For the deterministic model we have seen that when R0 > 1
the proportion infected is given by the non-trivial solution of
τ = 1 − e −τ R0 .
This holds true for the GSE in the supercritical case.
Scalia-Tomba (1985) presented an elegant way of doing this
using the Sellke construction and an imbedding representation
Consider the infectious pressure process An (t)
An (t) → λE (I )t in probability, uniformly on compact sets
√
D
n (An (t) − λE (I )t) −→ Wiener process, var=λ2 Var (I )t
)+λ2 Var (I )τ (1−τ )2
Then, w.p. 1 − q m , `n → N τ, τ (1−τ(1−(1−τ
as
2
)R0 )
n → ∞.
Provides an approximate way to evaluate L(` | λ)
28 / 33
Epidemics upon Random Graphs
Thus far, we have completely ignored any social structure that
may be present in the population. This is unrealistic.
We shall explore how some of the previous results transfer to
epidemics defined in structured populations.
These populations may be fixed or random (or both).
A natural way to start is by using a random graph as a model
of social network → huge area in sociology.
More pragmatic to assume closer contacts locally as opposed
to identical contacts with everyone.
All individuals involved are assumed identical. Multitype
models will be considered later.
29 / 33
Structured Epidemics: Two levels of mixing
Small social groups like households, schools and workplaces
are particularly important for disease transmission.
A general framework for epidemic local and global epidemic
spread was described in Ball et al 1997.
The population is partitioned into groups (households,
farms. . . ) and infected individuals can transmit the disease:
globally, with everyone, at the points of a Poisson process with
rate λG /N
locally, within group, at the points of a Poisson process with
rate λL
The ‘great circle’ variant is the first small world model (200 vs
11000 citations).
30 / 33
A very simple illustration
Two groups of 2 and 3 individuals respectively
31 / 33
Model Analysis
Ball et al 1997 derive a branching process approximation for
the early stages of the epidemic. Groups are (super)individuals
and
Each group has mean offspring (# infections) λG E (`), where
` = number infected in a ‘typical’ group.
A threshold parameter as the number of groups →P∞ is given
sµ π
by R∗ = λG E (`) = λG E (I )ν(λL ), where ν(λL ) = s v s s is
the average local final size if only local infections permitted
The process may explode if R∗ > 1.
The authors also derive a CLT for the final size and final
severity, should a ‘large’ outbreak occur. Can be extended to
other (appropriate) functionals like the total epidemic cost.
32 / 33
Notes on Additional Structure
The framework with local and global transmission on a fixed
population is very general.
Several extensions are being developed where the local or the
global population may be represented by a random network.
Threshold parameters are derived using similar techniques
Overlapping groups remain a challenge
Can also consider multitype epidemics.
33 / 33