* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Newtonian Mechanics * Momentum, Energy, Collisions
Laplace–Runge–Lenz vector wikipedia , lookup
Routhian mechanics wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Monte Carlo methods for electron transport wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Center of mass wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Angular momentum operator wikipedia , lookup
N-body problem wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Photon polarization wikipedia , lookup
Centripetal force wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Classical mechanics wikipedia , lookup
Moby Prince disaster wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Equations of motion wikipedia , lookup
Work (physics) wikipedia , lookup
Specific impulse wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Classical central-force problem wikipedia , lookup
Newtonian Mechanics –
Momentum, Energy, Collisions
Gernot Laicher
For ACCESS Class 2011
Quick Review: Vectors and Scalars
• Vectors: Magnitude and Direction
(e.g., Force, Displacement, Velocity, Acceleration)
• Scalars: Magnitude only
(e.g., Temperature, Altitude, Age)
Adding Vectors
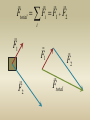
F1
Two forces are acting on a mass m:
How do we find the total force ?
F2
Ftotal Fi F1 F2
i
F1
F1
F2
F2
Ftotal
Subtracting Vectors
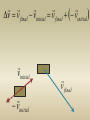
An object changes it’s velocity.
What is it’s change in velocity?
vinitial
v final
v v final vinitial v final vinitial
vinitial
vinitial
v final
v v final vinitial v final vinitial
v
v final
vinitial
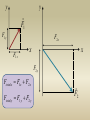
y
y
F1
F1 y
F2 x
F1 x
x
x
F2 y
Ftotal x F1 x F2 x
Ftotal y F1 y F2 y
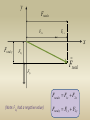
F2
y
Ftotalx
F2 x
F1 x
x
Ftotal y
F2 y
F1 y
Ftotal
Ftotal x F1 x F2 x
(Note: F2y had a negative value)
Ftotal y F1 y F2 y
Sir Isaac Newton
Godfrey Kneller’s 1689 portrait
of Isaac Newton (age 46)
(Source: http://en.wikipedia.org/wiki/Isaac_Newton)
Newton's First Law : An object at rest tends to stay at rest and an
object in uniform motion tends to stay in uniform motion unless
acted upon by a net external force.
Newton's Second Law: An applied force on an object equals the
rate of change of its momentum with time.
Newton's Third Law: For every action there is an equal and
opposite reaction.
Displaceme nt : r
dr
Velocity : v
dt
dv d dr
Acceleration : a
dt dt dt
dr r
Velocity : v
dt t
(as long as v const. during t )
dv v
Acceleration : a
dt t
(as long as a const. during t )
Momentum : p m v
Momentum of a car going 1mph (ignoring direction )
miles
p m v 1500 kg 1
hour
miles hour 1609.3 m
1500 kg 1
hour 3600 s
mile
m
1500 kg 0.447
s
kg m
kg m
670.5
670.5 2 s
s
s
670.5 N s
Momentum of a bullet going 948 m / s ( M 16 rifle )
m
p m v 3.9 g 948
s
kg
m
3.9 g
948
1000 g
s
m
0.0039kg 948
s
kg m
3. 7
s
3.7 Ns
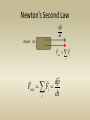
Newton’s Second Law
dp
dt
mass m
Fnet Fi
i
dp
Fnet Fi
dt
i
dp
Fnet Fi
dt
i
d
mv
dt
dm
dv
v m
dt
dt
dm
v ma
dt
For a non-changing mass:
a
m
Fnet ma
Fnet
dm
0
dt
Rewriting Newton’s Second Law
dp (" Change in Momentum" )
m
Fnet
Fnet dt (" Impulse" )
dp
dt
Fnet dt dp
Impulse = Change in Momentum
Example: A constant force of 5N applied for 0.5
seconds on a mass of 0.2kg, which is initially at rest.
Fnet dt dp
0.5 s
0s
0.5 s
0.5 s
Fnet dt Fnet dt Fnet 0.5s
0s
0s
Fnet dt
p fin a l
dp
pin itial
p fina l
dp p final pinitial
pinitial
5 N 0.5s mv final mvinitial 2.5 Ns 0.2kg v final
m
v final 12.5
s
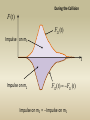
In general, the force may depend on time
Fnet t dt dp
t fin a l
Fnet t dt
tin itia l
Fnet (t )
p fin a l
dp
pin itia l
t fina l
Fnet t dt
t initial
t
Impulse = “Area” under the F(t) curve
(Integrate F(t) over time to get the impulse)
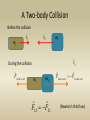
A Two-body Collision
Before the collision
m1
v2
v1
v2
During the collision
F from 2 on 1
m2
m1
m2
F12 F21
Ffrom1 on 2 Ffrom 2 on 1
(Newton’s third law)
During the Collision
F (t )
F21(t )
Impulse on m1
t
Impulse on m2
F12 (t ) F21(t )
Impulse on m2 = - Impulse on m1
Impulse on m2 = - Impulse on m1
Change of momentum of m2 = - Change of momentum of m1
p2 p1
p2 final p2 initial p1 final p1 initial
p1 final p2 final p1 initial p2 initial
Total momentum after collision = Total momentum before collision
The total momentum of the system is “conserved” during the collision.
(This works as long as there are no external forces acting on the system)
After the collision
u1
m1
m2
u2
p1 final p2 final p1 initial p2 initial
For a 1-dimensional collision we can replace the
vector with + or – signs to indicate the direction.
m1u1 m2u2 m1v1 m2v2
Note: u1, u2, v1, v2 may be positive or negative, depending on
direction and depending on your choice of coordinate system.
m1u1 m2u2 m1v1 m2v2
Given: m1 , m2 , v1 , v2
What can we find out about the final velocities u1 and u2 ?
m1u1 m2u2 m1v1 m2v2
Given: m1 , m2 , v1 , v2
What can we find out about the final velocities u1 and u2 ?
Answer: In general there are an infinite number of possible
solutions (combinations of the final velocities u1 and u2 that
fulfill the conservation of momentum requirement). Which of
those solutions really happens depends on the exact nature
of the collision.
Excel Program – Using a Solver
1) Solving a simple math problem (2x + 6y =14) infinitely many solutions
2) Adding a constraint (a second equation) (x+y=3) to get a single solution.
3) Solving a quadratic equation (4x2 + 2x =20) how many solutions?
4) Pick different initial conditions for x to find all the solutions.
5) Write an Excel program that has the following input fields:
m1, m2 , v1 , v2 , u1 , u2 .
6) Create (and label) fields that calculate p1initial , p2initial , p1final , p2final .
7) Create (and label) fields that calculate ptotal initial , ptotal final.
8) Create (and label) fields that calculate ptotal final - ptotal initial.
9) Fill in these values: m1=1 (kg), m2=1 (kg), v1=1 (m/s), v2=-1 (m/s),
u1=some value (m/s), u2=some value (m/s).
10) Use a solver that changes u1 and u1 and makes
ptotal final - ptotal initial = 0.
How many possible solutions can you find?
Mechanical Energy of Two Mass System
Before the collision
1
1
2
Einitial m1v1 m2 v22
2
2
After the collision
1
1
2
E final m1u1 m2u22
2
2
Totally Elastic Collision:
E final Einitial
(no mechanical energy is lost)
E final Einitial 0
1
1
1
2
2 1
2
2
m1u1 m2u2 m1v1 m2 v2 0
2
2
2
2
Excel Program – Using a Solver
Add the following to your Excel “Collision-Solver”:
Create fields that calculate
Etotal initial ,
Etotal final ,
Etotal final - Etotal initial ,
% Energy change.
% Energy Change
E final Einitial
Einitial
100
Now solve your collision problem again. This time, use the constraint
Etotal final - Etotal initial = 0
Find all possible solutions and interpret their meaning.
Totally Inelastic Collision: u1 final u2 final u final
(The two masses stick together after the collision and move with the same velocity)
Conservati on of momentum : m1 m2 u m1v1 m2v2
m1v1 m2 v2
u
m1 m2
Is there Mechanical Energy Conservation in Totally
Inelastic Collisions?
mv m v
u
1 1
2 2
m1 m2
m1v1 m2 v2
1
1
2
E final (m1 m2 )u (m1 m2 )
2
2
m1 m2
1
1
2
Einitial m1v1 m2 v22
2
2
2
Excel Program – Using a Solver
Name the Excel worksheet tab for the previously created elastic
collision “Elastic Collision”.
Make a copy of this tab and rename it “Inelastic Collision”
Modify the “Inelastic Collision” tab so that it calculates “u1” from the
initial conditions (masses, initial velocities) according to the formula
for u on the previous page. Then you can make u2=u1. So now both
u1 and u2 will always have the same value.
Use a lab notebook to record your
findings and investigate several
scenarios of collisions
For both elastic and inelastic collisions you should find solutions for
these cases:
1) Equal masses, one mass initially at rest.
2) Equal masses, equal but opposite velocities (head on collision).
3) Very unequal masses, lighter mass at rest.
4) Very unequal masses, heavier mass at rest.
5) Very unequal masses, equal but opposite velocities (head on
collision)