Download What is Circular Motion?

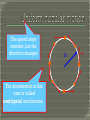
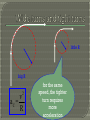
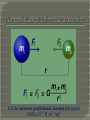
 Motion
of an object travelling at constant
speed in a circle
 Let’s explore the kinematics of circular
motion.
 Why is it accelerating, if the speed is
constant?
 What would cause an object to move in a
circle?
 Objects
move in a straight line at a constant
speed unless a force acts on them. This is
Newton's First Law.
 However, many
things move in curved paths,
especially circles, and so there must be a
force acting
on them to pull them out
of their straight line paths
and make them turn
corners.
 We
call the force that makes objects
move in a circle the CENTRIPETAL
FORCE(the name comes from Latin and
means centre-seeking)
 How is Centripetal Force related to:
• Mass of object?
• Velocity of object?
• Radius size of circle?
• Let’s Explore!
The speed stays
constant, but the
direction changes
The acceleration in this
case is called
centripetal acceleration
R
v
little R
big R
2
v
aC =
R
for the same
speed, the tighter
turn requires
more
acceleration
 Remember: Speed
= Distance/Time
 Let’s define Period (T) as the time it takes
the object to travel once around the
circle.
 How far does it travel in one rotation?
 Therefore:
The tension in the string
provides the necessary
centripetal force to keep
the ball going in a circle.
path of ball if the string
breaks
 What
is the tension in a string used to twirl a
0.3 kg ball at a speed of 2 m/s in a circle of
1 meter radius?
 Force = mass x acceleration [ m  aC ]
 acceleration aC = v2 / R = (2 m/s)2/ 1 m
= 4 m/s2
 force = m aC = 0.3  4 = 1.2 N
 If the string is not strong enough to handle
this tension it will break and the ball goes
off in a straight line.



On a flat, level curve, the
friction between the tires
and the road supplies the
centripetal force.
If the tires are worn
smooth or the road is icy
or oily, this friction force
will not be available.
The car will not be able to
move in a circle, it will
keep going in a straight
line and therefore go off
the road.
 The
object on
the dashboard
straight line
object
naturally
follows
red object will make
the turn only if there is
enough friction on it
 Otherwise it goes straight
 The apparent outward
force is called the
centrifugal force
 It is NOT A REAL force!
 An object will not move
in a circle until something
makes it, in this case the
car door!
 Sir
Isaac Newton discovered that every
particle attracts every other particle in
the universe with a force when he saw an
apple fall from a tree towards the earth.
 The force of attraction between any two
particles in the universe is called
Gravitation or gravitational force
G is the universal gravitational constant and equals
6.673 x 10-11 N m2 / kg2
 Always
distinguish between G and g
 G is the universal gravitational constant
• It is the same everywhere
g
is the acceleration due to gravity
• g = 9.80 m/s2 at the surface of the Earth
• g will vary by location
The moon is actually
falling toward Earth
but has great enough
tangential velocity
to avoid hitting
Earth.
If the moon did not
fall, it would follow a
straight-line path.
1571 – 1630
 German astronomer
 Best known for
developing laws of
planetary motion

• Based on the
observations of Tycho
Brahe

Kepler’s First Law
• All planets move in elliptical orbits with the Sun at one
focus

Kepler’s Second Law
• The radius vector drawn from the Sun to a planet sweeps
out equal areas in equal time intervals

Kepler’s Third Law
• The square of the orbital period of any planet is
proportional to the cube of the semimajor axis of the
elliptical orbit




Can be predicted from
the inverse square law
Start by assuming a
circular orbit
The gravitational force
supplies a centripetal
force
Ks is a constant
GMSunMPlanet MPlanetv 2

2
r
r
2 r
v
T
2

 3
4

2
3
T 
 r  KS r
 GMSun 

Using the distance between the Earth and the Sun,
and the period of the Earth’s orbit, Kepler’s Third
Law can be used to find the mass of the Sun
MSun

4 2r 3

GT 2
Similarly, the mass of any object being orbited can
be found if you know information about objects
orbiting it