Download Physics 416G : Solutions for Problem set 11

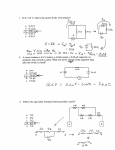
Physics 416G : Solutions for Problem set 11
Due : December 2, 2015
Please read Griffiths sections 7.1, 7.2, pages 296 - 332.
We covered the material from slightly different point of view in the class.
Please show all the details of your computations including intermediate steps.
1
Problem 1
A long solenoid with radius R and N turns per unit length carries a time-dependent current I(t) in the
ϕ̂ direction. Find the electric field (magnitude and direction) at a distance ρ from the axis (both inside
and outside the solenoid), in the quasistatic approximation, where the magnetostatics are applicable
for practical computations. (Electromagnetic waves and radiation effects are not very strong.)
~ = µ0 N I ẑ for the magnetic field inside the solenoid, while it
Sol: In the quasistatic approximation, B
vanishes outside. Thus using the Ampère loop inside the solenoid, we have Φ = Bπρ2 = µ0 N Iρ2 . Thus
I
~ = − dΦ = − µ0 N ρ dI ϕ̂ .
~ · d~l = E2πρ = − dΦ = −µ0 N πρ2 dI
→
E
E
dt
dt
dt
2 dt
Similar computation gives for the outside as
I
~ · d~l = E2πρ = − dΦ = −µ0 N πR2 dI
E
dt
dt
2
→
2
~ = − dΦ = − µ0 N R dI ϕ̂ .
E
dt
2ρ dt
Problem 2
A capacitor C has been charged up to potential V0 . At time t = t0 , it is connected to a resistor R, and
begins to discharge. See the left figure.
a) Determine the charge on the capacitor as a function of time, Q(t). What is the current through the
resistor, I(t)?
b) What was the original energy stored in the capacitor? By integrating the power P = V I = I 2 R,
confirm that the heat delivered to the resistor is equal to the energy lost by the capacitor.
Now imagine charging up the capacitor, by connecting it (and the resistor) to a battery of fixed
voltage V0 , at time t = t0 . See the right figure.
c) Again, determine Q(t) and I(t).
R
d) Find the total energy output of the battery ( V0 Idt). Determine the heat delivered to the resistor.
What is the final energy stored in the capacitor? What fraction of the work done by the battery shows
up as energy in the capacitor?
Q
Sol: a) We use V = Q/C = IR, and thus dQ
dt = −I = − RC . The negative sign comes from the fact that
the charge on the capacitor is decreasing. The solution can be easily found to be Q(t) = Q0 e−(t−t0 )/RC .
From the initial condition Q0 = Q(t0 ) = CV0 , we arrive Q(t) = CV0 e−(t−t0 )/RC . The current is
V0 −(t−t0 )/RC
derivative of the charge with negative sign. I(t) = − dQ
.
dt = R e
b) The original energy stored in the capacitor is nothing but W = 12 CV02 . The energy delivered to the
resistor is
Z ∞
Z ∞
Z
V 2 ∞ −2(t−t0 )/RC
1
e
dt = CV02 .
P dt =
I 2 Rdt = 0
R t0
2
t0
t0
c) For this problem we need to include both the contributions of the capacitor and resistor. Thus we
CV0 −Q
get V0 = Q/C + IR. This gives dQ
dt = I =
RC . We have positive sign because positive current
means increasing charge Q at the capacitor. Thus
dQ
dt
=−
,
Q − CV0
RC
→
Q(t) = CV0 1 − e−(t−t0 )/RC .
V0 −(t−t0 )/RC
Taking a derivative with respect to t, we arrive I(t) = dQ
.
dt = R e
d) The energy from battery can be obtained as
∞
Z ∞Z
Z
V 2 ∞ −(t−t0 )/RC
V2
V2
V0 Idt = 0
e
dt = 0 (−RC)e−(t−t0 )/RC = 0 RC = CV02 .
R t0
R
R
t0
t0
Since I(t) is the same as in a), the energy delivered to the resistor is again 12 CV02 . The final energy in
the capacitor is also 21 CV02 , so half the energy from the battery goes to the capacitor, and the other
half to the resistor.
3
Problem 3
During the class we considered the magnetic induction of a current loop to derive the meganetostatic
energy. Let us consider two loops of wire at rest. If we run a steady current I1 around the loop 1, it
~ 1 . Some of the field lines will pass trough the loop 2. Let magnetic flux Φ2
produces a magnetic field B
~
be the flux of B1 through 2. Thus we conclude that
Z
Φ2 =
~ 1 · dS
~2 ,
B
~ 1 = µ0 I1
B
4π
I
d~l1 × (~x − ~x0 )
,
|~x − ~x0 |3
(1)
~2 is the area of the loop 2. We notice that the magnetic field B
~ 1 is proportional to I1 . See the
where S
first figure. Thus we can set
Φ2 = M21 I1 ,
where M21 is called mutual inductance, compared to L which is the ‘self’ inductance.
a) Starting from the expression (1), derive an expression of M21 in terms of the line integrals of two
loops. You can use Stokes theorem and the expression of vector potential.
b) Argue that the mutual inductance has the property M12 = M21 .
c)A short solenoid (length l and radius a, with na turns per unit length) lies on the axis of a very
long solenoid (radius b, nb turns per unit length). See the lower figure. Current I flows in the short
solenoid. What is the flux through the long solenoid? What is the mutual inductance?
Now, consider a small loop of wire (radius R1 ) lies a distance z above the center of a large loop
(radius R2 ). The planes of the two loops are parallel, and perpendicular to the common axis.
d) Suppose current I flows in the large loop. Find the flux through the small loop. (The small loop is
so small that you may consider the field of the big loop to be essentially constant.)
e) Suppose current I flows in the small loop. Find the flux through the large loop. (The small loop is
so small that you may treat it as a magnetic dipole.)
f) Find the mutual inductances, and confirm that M12 = M21 .
Sol: a) This can be done as
Z
Z
I
~ 1 · dS
~ 2 = (∇
~ ×A
~ 1 ) · dS
~2 = A
~ 1 · d~l2 ,
Φ2 = B
I
=
I
µ0
I1
4π
I I ~ ~
d~l1
dl1 · dl2
~l2 = µ0 I1
·
d
,
|~x − ~x0 |
4π
|~x − ~x0 |
where we use
~ 1 = µ0 I1
A
4π
I
d~l1
.
|~x − ~x0 |
Thus we get
M21 =
µ0
4π
I I
d~l1 · d~l2
.
|~x − ~x0 |
b) One can compute the magentic flux Φ1 from the current loop 2 and the results would be the same
except changing the current I2 to I1 . Whatever the shapes and positions of the loops, the flux through
2 when we run a current I around 1 is identical to the flux through 1 when we send the same current
1 around 2.
c) Since the inner solenoid is short, it has a very complicated field. It puts a different amount of flux
through each turn of the outer solenoid. It would be a miserable task to compute the total flux this
way. However, if we use the equality of the mutual inductances argued in b), the problem becomes
easy. Let us consider the reverse situation: run the current I through the outer solenoid, and calculate
the flux through the inner one. The field inside the long solenoid is B = µ0 nb I, so the flux through
a single loop of the short solenoid is Bπa2 = µ0 nb Iπa2 . There are na l turns in all, so the total flux
through the inner solenoid is Φ = µ0 πa2 na nb lI. This is also the flux a current I in the short solenoid
would put through the long one, which is what we set out to find. Thus the mutual inductance is
M = µ0 πa2 na nb l.
~ =
d) We already computed the magentic field due to a current loop on the current loop axis as B
2
R
µ0 I
2
2 (R2 +z 2 )3/2 ẑ. Thus the flux through the small loop is
2
Z
Φ=
πR12 R22
~ ·B
~ = µ0 I
dS
.
2 (R22 + z 2 )3/2
~ = µ0 m3 (2 cos θr̂ + sin θθ̂, where
e) The magnetic field due to a magnetic monopole is given by B
4π r
2
m = IπR1 . It is convenient to use spherical coordinate to compute the area contribution for the
magnetic field. Integrating over the spherical “cap,” which is bounded by the large loop and centered
at the small loop, we get
θ̄
µ0 IπR12 sin2 θ µ0 πR12 R22 I
Φ=
r sin θdθdφ(2 cos θ) =
=
.
r
2 0
2(R22 + z 2 )3/2
p
Here we use sin θ̄ = R2 /r with r = R22 + z 2 . The result is the same as d)
f) Thus
µ0 πR12 R22
M12 = M21 =
.
2 (R22 + z 2 )3/2
Z
4
2
~ · dS
~ = µ0 IπR1
B
4π r3
Z
2
Problem 4
a) A capacitor C is charged up to a potential V0 and connected to an inductor L. as shown in the left
figure. At time t = t0 , the switch S is closed. Find the current in the circuit as a function of time.
How does your answer change if a resistor R is included in series with C and L?
b) Suppose the circuit in the right figure has been connected for a long time when suddenly, at time
t = t0 , switch S is thrown, bypassing the battery.
i) What is the current at any subsequent time t?
ii) What is the total energy delivered to the resistor?
iii) Show that this is equal to the energy originally stored in the inductor.
Q
Sol: a) The electromotive force is given by the expressions E = −L dI
dt = C , where Q is the charge on the
capacitor, I =
dQ d2 Q
dt . dt2
1
= − LC
Q = −ω 2 Q, where ω =
√1 .
LC
The general solution is Q(t) = A cos ω(t−
t0 )+B sin ω(t−t0 ). At t = t0 , Q = CV , thus A = CV . I(t) = dQ
dt = −Aω sin ω(t−t0 )+Bω cos ω(t−t0 ).
At t = t0 , I = 0. Thus B = 0 and
r
C
t − t0
I(t) = −CV ω sin ω(t − t0 ) = −V
sin √
.
L
LC
If you put in a resistor, the oscillation is “damped.” Thus the equation turns into −L dI
dt =
L
Q
C
+ IR, so
1
dQ
d2 Q
+ Q = 0.
+R
dt2
dt
C
b) Initial current is the current due to E0 and R, and thus I0 = ER0 .
i) Now bypassing the battery, we have the equation −L dI
dt = IR. The equation for I can be easily
−R(t−t0 )/L
solved to give I = I0 e
, where we use the initial condition I = I0 at t = t0 . Thus
I(t) =
E0 −R(t−t0 )/L
e
.
R
ii) The total energy delivered to the resistor can be computed by integrating the power over the time.
E02 −2R(t−t0 )/L
2
. Thus we have
The power is given by dW
dt = P = I R = R e
W =
E02
R
Z
∞
e−2R(t−t0 )/L =
t0
LE02
.
2R2
iii) The original store energy is given by
W0 =
1 2
LE02
LI0 =
.
2
2R2
Thus they are the same.
5
Problem 5 : Transformer (Bonus problem, optional)
a) Two coils are wrapped around a cylindrical form in such a way that the same flux passes through
every turn of both coils. (In practice this is achieved by inserting an iron core through the cylinder;
this has the effect of concentrating the flux.) The “primary” coil has N1 turns and the secondary has
N2 as in the figure. If the current I in the primary is changing. show that the emf in the secondary is
given by
E2
N2
=
,
E1
N1
where E1 is the (back) emf of the primary. [This is a primitive transformer, which is a device for raising
or lowering the emf of an alternating current source. By choosing the appropriate number of turns,
any desired secondary emf can be obtained.]
b) The transformer takes an input AC voltage of amplitude V1 , and delivers an output voltage of
amplitude V2 , which is determined by the turns ratio (V2 /V1 = N2 /N1 ). If N2 > N1 the output voltage
is greater than the input voltage. Why doesn’t this violate conservation of energy?
c) In an ideal transformer the same flux passes through all turns of the primary and of the secondary.
Show that in this case M 2 = L1 L2 , where M is the mutual inductance of the coils. and L1 , L2 are
their individual self-inductancs.
d) Suppose the primary is driven with AC voltage Vin = V Icos(ωt), and the secondary is connected
to a resistor, R. Show that the two currents satisfy the relations
L1
dI2
dI1
+M
= V1 cos(ωt) ,
dt
dt
L2
dI2
dI1
+M
= −I2 R .
dt
dt
e) Using the result in c), solve these equations for I1 (t) and I2 (t). (Assume I1 has no DC component.)
f) Show that the output voltage (Vout = I2 R) divided by the input voltage (Vin ) is equal to the turns
ratio: Vout /Vin = N2 /N1 .
g) Calculate the input power (Pin = Vin I1 ) and the output power (Pout = Vout I2 ), and show that their
averages over a full cycle are equal.
Sol: a) Let be the flux of B through a single loop of either coil, so that Φ1 = N1 Φ and Φ2 = N2 Φ.
Then
Φ
Φ
E1 = −N1 ,
E2 = −N2 .
dt
dt
2
Thus we get the relation EE21 = N
N1 .
b) Power is the product of voltage and current. Thus if the voltage goes up, the current must go down.
The purpose of this problem is to see exactly how this works out, in a simplified model.
c) Suppose current I1 flows in coil 1, and I2 in coil 2. If Φ is the flux through one turn,
Φ1 = I1 L1 + M I2 = N1 Φ ,
Φ1 = I2 L2 + M I1 = N1 Φ .
Thus Φ = (I1 L1 +M I2 )/N1 = (I2 L2 +M I1 )/N2 . These satisfy for any I1 and I2 . Thus L1 /N1 = M/N2
and M/N1 = I2 /N2 . Diving one form the other, we get M 2 = L1 L2 .
d) The emf is the combination of the self inductance and mutual inductance. Thus we get
−E1 =
dΦ1
dI1
dI2
= L1
+M
= V1 cos(ωt) ,
dt
dt
dt
−E2 =
dΦ2
dI2
dI1
= L2
+M
= −I2 R .
dt
dt
dt
dI2
1
e) Multiplying the first equation by L2 , we get L2 L1 dI
dt + M L2 dt = L2 V1 cos(ωt). Plugging in
dI2
dI1
dI1
2 dI1
L2 dt = −M dt − I2 R, we get M dt + M (−M dt − I2 R) = L2 V1 cos(ωt). This gives
I2 (t) = −
L2 V1
cos(ωt).
MR
L 2 V1
1
We plug back this to the first equation to get the equation for I1 as L1 dI
dt + M M R ω sin(ωt) =
V1 cos(ωt). Now we can solve the I1 easily.
V1 1
L2
I1 (t) =
sin(ωt) +
cos(ωt) .
L1 ω
R
f) The ratio of the amplitude is
Vout
I2 R
L2 V1
R
L2
N2
=
=−
cos(ωt)
=−
=−
.
Vin
V1 cos(ωt)
MR
V1 cos(ωt)
M
N1
g) The input power is
Pin
V1
= Vin I1 = V1 cos(ωt)
L1
1
L2
V12
1
L2
2
sin(ωt) +
cos(ωt) =
sin(2ωt) +
cos (ωt) ,
ω
R
L1 2ω
R
while the output power is
Pout = Vout I2 = I22 R =
L22 V12
cos2 (ωt) .
M 2R
Taking the average we get
hPin i =
V12 L2
,
2L1 R
hPout i =
L22 V12
V12 L2
=
= hPin i ,
2M 2 R
2L1 R
where we use the average of cos2 (ωt) is 1/2 and the average of sin(ωt) cos(ωt) is 0.
6
Problem 6 : Betatron (Bonus problem, optional)
a) Let us consider the motion of a charged particle in a strong magnetic field, which is a circular
motion. This can be achieved with the magnetic force providing the centripetal acceleration as in the
~ points into the page. If the charge q moves counterclockwise,
left figure. A uniform magnetic field B
with speed v, around a circle of radius R, Find the momentum of the particle.
b) Electrons undergoing cyclotron motion can be speeded up by increasing the magnetic field. The
accompanying electric field will impart tangential acceleration. This is the principle of the betatron.
One would like to keep the radius of the orbit constant during the process. Show that this can be
achieved by designing a magnet such that the average field over the area of the orbit is twice the field
at the circumference. See the figure. Assume the electrons start from rest in zero field, and that the
apparatus is symmetric about the center of the orbit. (Assume also that the electron velocity remains
well below the speed of light, so that nonrelativistic mechanics applies.)
~ points inward, and has a fixed magnitude qvB. To sustain
Sol: a) The magnetic force F~ = q~v × B
uniform circular motion, this should be the same as the centripetal acceleration mv 2 /R. Thus
qvB = mv 2 /R,
where m is the particle’s mass. Thus the momentum is p = mv = qBR. This is known as the cyclotron
formula because it describes the motion of a particle in a cyclotron-the first of the modem particle
accelerators. It also suggests a simple experimental technique for finding the momentum of a particle:
send it through a region of known magnetic field, and measure the radius of its circular trajectory.
This is in fact the standard means for determining the momenta of elementary particles.
b) If R is to stay fixed, we have the following relation by taking a derivative of the formula in a) as
qR
dB
dv
=m
= ma = F = qE ,
dt
dt
→
E=R
dB
.
dt
Now we use Faraday’s law to get the field as
I
dΦ
~ · d~l = 2πRE = 2πR2 dB
−
= E
dt
dt
→
B=−
Φ
Φ
+ const. = −
.
2
2πR
2πR2
Where we use the initial condition that at t = 0, the field is zero and thus const. = 0. Thus the field
at R must be half the average field over the cross-section of the orbit.