Download Ch.20 Induced voltages and Inductance Faraday`s Law

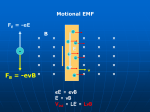
Ch.20
Induced voltages and Inductance
Faraday’s Law
• Last chapter we saw that a current produces a
magnetic field.
• In 1831 experiments by Michael Faraday and
Joseph Henry showed that a changing
magnetic field could induce a current in a
circuit.
Faraday’s setup.
Switch
Ammeter
0.0 mA
+
_
Battery
• The coil with the switch is connected to a battery.
(Primary coil)
• When current goes through a coil, it produces a
magnetic field.
• The coils are wrapped around an iron ring to
intensify the magnetic field.
• The secondary coil is hooked up to an ammeter.
This coil is not hooked up to a battery.
When the switch in the primary coil is closed,
the ammeter reads a current in the secondary
coil for a short moment, then returns to zero.
When the switch is opened, the ammeter
momentarily measures a current in the
opposite direction before returning to zero.
When there is a steady current in the primary
coil, there is no current read by the ammeter.
• Conclusion: An electric current can be
produced from a changing magnetic field.
• The current produced in the secondary coil
occurs only for the instant the magnetic field
through the secondary coil is changing.
• The secondary circuit behaves as though a
source of emf (a battery) was connected to it
for a short time.
• An induced emf is produced in the secondary
circuit by the changing magnetic field.
emf – electric motive force, not really a force.
This is a source of electrical work/energy per
unit charge.
work/charge = volt
Devices that increase the potential energy of
circulating charges (batteries, generators) are
sources of emf.
Think of emf as a voltage increase.
While the magnetic field inside the secondary
coil was changing, the secondary coil acted as
is it was connected to a battery.
The changing magnetic field induced an
electric field in the secondary wire that caused
the current to flow.
Changing magnetic fields induce electric fields.
A constant magnetic field can also induce an
electric field. Example of this is an electric
generator.
If the magnetic field is constant then what is
changing?
The property that creates an electric field is the
changing of the magnetic flux.
Magnetic flux
Magnetic flux is defined in the same way electric
flux was defined earlier.
Magnetic flux through a loop, is proportional
to the strength of the B-field passing through
the plane of the loop and the area of the loop.
B = B A cos
B cos is the component of the B-field that is
perpendicular to the loop.
B
side view of loop
Magnetic flux
• The value of the magnetic flux is proportional
to the number of B-field lines passing through
the loop.
•
= B A cos is maximized when = 0. This is
when the B-field is perpendicular to the loop.
B
• see fig. 20.3 for maximizing/minimizing the flux
• see example 20.1
Faraday’s law of Induction
Consider a wire loop connected to an ammeter.
Moving a magnet towards the loop will induce a
current in one direction.
When the magnet is stationary, there is no
induced current.
Moving the magnet away from the loop induces
a current in the opposite direction.
This is similar to the Faraday experiment shown earlier.
Faraday’s Law of induction
• An emf is induced in a cicuit when the
through the circuit changes with time.
B
• The instantaneous emf induced in a circuit
equals the negative rate of change of B with
respect to time.
• This is Faraday’s Law of magnetic induction.
N
B
t
Lenz’s Law: The induced current travels in the
direction that creates a magnetic field with
flux opposing the change in the original flux
through the circuit.
If the flux is increasing in one direction, the
induced current will be in the direction so that
its own magnetic flux will be in the direction
opposite of the original flux.
Nature wants to keep the flux constant.
The induced magnetic flux does not have to be
in the opposite direction of the original flux.
Fig. 20.5. The original flux is upwards. As the
B-field is reduced in strength, the flux is
reduced. Lenz’s law will show that the
induced current will be in the direction so that
the induced B-field is in the upward direction.
work out example 20.2
Application of Faraday’s law
• Ground fault interrupters, used to protect
against short circuits
• Pickups on electric guitars, converts the
vibrations of the strings to an electrical signal.
Motional emf
• Earlier we changed the B-field with time.
• Now we keep the field constant. Look at the
emf induced in a conductor moving through a
magnetic field.
1st look at straight conductor of length (L) moving with
constant velocity through a uniform B-field pointing
into the page.
In this example the velocity is normal to B-field.
Force on the electrons (-) is FB = qvB downward
Free electrons build up on the lower end, leaving a net
positive charge on the upper end. This produces an
E-field in the conductor.
Electrons keep moving until the magnetic force is
balanced out by the electric force qE.
qE = qvB
or E = vb
The potential difference across the conductor is
given by V = E L
so V = EL = BLv
The upper end of the conductor will be at a
higher potential than the lower end.
Now the conductor is part of a closed loop.
See pictures on page 667.
Conducting bar of length L slides along two fixed
parallel conducting rails. Let the stationary part of
the loop have a resistance R. A uniform and constant
B-field is perpendicular to the plane of the loop.
As the bar is pulled to the right, a magnetic force
acts on the free charges in the bar. Since the bar is
part of a closed loop, an induced current circulates.
The change in B and the induced current are
produced from the change in area of the loop
as the bar moves.
If bar moved a distance x in time t, the flux
changes as
B.
( A = L x)
B =B A = BL x
using Faraday’s Law with 1 loop (N = 1) and
ignoring the direction for now
B
t
x
BL
t
BLv
We call this motional emf since it is produced
from the motion of a conductor through a
magnetic field.
if we want to find the induced current, we use
the resistance of the circuit R.
V = IR I = V/R
I
R
BLv
R
gives the magnitude of the induces current.
Use Lenz’s Law and right hand rule to get
direction.