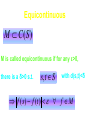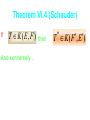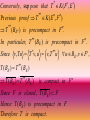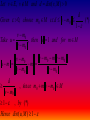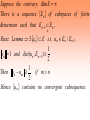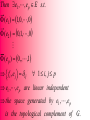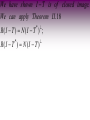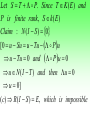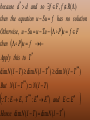* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download AAN_15
Survey
Document related concepts
Transcript
Chapter 6
Compact operators
Spectral Decomposition of
self-adjoint compact operators
VI.1 Definition. Elementary
Properties Adjoint
Compact Operator
Let E and F be Banach spaces
An operator
T LE, F
is called compact if
T BE
every seq.
has conv.
subseq.
is precompact
K(E,F) is the family of compact operators
in L(E,F); K(E,E)=K(E)
Theorem VI . 1
K(E,F) is a closed vector subspace of L(E,F).
for the norm
L( E , F )
K E , F is obviously vector subspace of L( E , F ).
Suppose Tn K ( E , F ), T L( E , F ) with Tn T
L( E ,F )
0
Since F is complete, it is sufficient to show that
for any 0, T BE is cov ered by a finite number
of ball B f i , . Fix n such that Tn T
Tn BE B f i , where I is finite
2
iI
T BE B f i ,
iI
T is compact .
L( E ,F )
2
and
Finite Rank
An operator
finite rank if
T L( E , F )
is called
dim R(T )
A continuous operator T of finite rank is
compact.
Corollary VI. 2
Let
Tn
be a sequence of continuous
operators of finite rank from E to F and
T L( E , F )
Tn T
0
L( E , F )
such that
then
T K (E, F )
Remark 1
p.1
The family << problem of approximation>>
(Banach, Grothendieck) concerns the
converse of Corollary VI.2 . Given a compat
operator T, does there exist a sequence
Tn
Tn T
of operators of finite rank such that
0
L( E , F )
?
Remark 1
p.2
In general, the answer is negative
(Enflo, 1972) – even for certain closed
vector subspace of
(1 p , p 2)
p
see for example Lindenstrauss- Tzafriri [2]
However the answer is affirmative in many
cases; for example of F is Hilbert
Let K T BE , being compact , can be cov ered by
B fi , , I is finite. Let G be the vector subspace
iI
generated by f i ' s and
let T PG T (T is of
finite rank )
T is compact . To show that T T 2
If x BE , then i0 I s.t. Tx f i (1)
0
then PG Tx PG f i
0
T x f i
0
( 2)
(1) ( 2) T x Tx 2
T T 2
x BE
Remark 1
p.3
From this proof, it follows that if F is
Schauder basis; then the answer is
affirmative.
Remark 2
p.1
Let us indicate also a technique quite useful
in nonlinear analysis which permits to
approximate a continuous map (linear or
nonlinear) by non-linear map of finite rank.
Remark 2 p.2
Let X be a Topology space, F is a Banach
space and
T:X F
is continuous
map such that T(X) is precompact in F.
Then for any
map
0,
there is a continuous
T : X F
of finite rank s.t.
T ( x ) T ( x ) x X
In
fact, K T ( X ), being compact , can be cov ered
by a
finite number of
K B ( f i , ) , I is
2
iI
Definite T by
T ( x )
qi ( x ) f i
iI
qi ( x )
balls.
finite
x X
iI
where qi ( x ) max Tx f i ,0
T ( x ) T ( x )
qi ( x ) f i
iI
qi ( x )
iI
qi ( x ) f i T ( x )
iI
qi ( x )
iI
T ( x)
qi ( x )( f i T ( x ))
iI
qi ( x )
iI
Proposition VI.3
Let E, F and G be Banach spaces.
If
T L( E , F )
[ resp. T K ( E , F )
then
and
and
S K (F ,G)
S L( F , G )
S T K ( E,G)
]
Equicontinuous
M C (S )
M is called equicontinuous if for any ε>0,
there is a δ>0 s.t.
s, t S
with d(s,t)<δ
f ( s ) f (t ) f M
Theorem (Arzelá-Ascoli)
A closed set
M C (S )
if and only if
(i) M is bounded on C(S)
(ii) M is equicontinuous
is compact
Theorem VI.4 (Schauder)
If
T K (E, F )
And conversely .
then
T K ( F , E)
*
To show that T * ( BF ) is precompact. Let vn BF ,
we show that one can extract a subsequence s.t
T *v n
k
converges in E . Let K T ( BE ), compact in F ,
Let H C ( K ) defined by
H n : x K vn , x ; n 1,2,
H satisfies the conditions of Artzela ' Ascoli Theorem
(i ) sup n ( x ) sup vn , x sup vn
xK
xK
xK
F
x vn
F
T T
(ii) Equicontinuous :
n ( x ) n ( y ) vn , x y vn x y x y
There is a subsequence n ( x ) of H s.t.
k
n converges in C ( K ) to a function ( x ).
k
In particular,
sup vn , Tu (Tu ) 0
k
uBE
as k
sup vn , Tu vn , Tu 0
k
uBE
sup T vn T vn , u 0
*
*
k
uBE
T vn T vn
*
*
k
E
0
k
as k ,
as k ,
T vn converges in E .
*
as k ,
Conversely, sup pose that T K ( F , E )
*
Pr evious proof T ** K ( E , F )
T ( BE ) is precompact in F .
**
In particular, T ** ( BE ) is precompact in F .
Since
v, Tu T *v, u v, T **u
u BE , v F ,
T ( BE ) T ** ( BE )
T ( BE ) T ( BE )
**
is compact in F
Since F is closed , T ( BE ) F
Hence T ( BE ) is precompact in F
Therefore T is compact .
VI.2 The Riesz-Fredholm
Theory
Lemma VI.1 (Riesz-Lemma)
Let E be a normed vector space and
be a closed vector subspace with
Then
u 1
0 , u E
and
M E
M E
such that
dist(u, M ) 1
Let v E , v M and d dist( v, M ) 0
d
Given 0, choose m0 M s.t.d v m0
(*)
1
v m0
Take u
, then u 1 and for m M
v m0
v m0 m v m0
v m0
um
m
v m0
v m0
d
v m0
, sin ce m0 m v m0 M
1 , by (*)
Hence dist(u, M ) 1
Remark
If dimM<∞ (or more generally if M is reflexive)
we can choose
0
in Lemma VI.1;
But not in general case (see [BT])
Theorem VI.5 (Riesz)
Let E be a normed vector space such that
BE
is precompact. Then E is of finite
dimension.
Suppose the contrary. dim E
There is a sequence En of subspaces of
finite
dim ension such that En 1 En ,
Riesz Lemma un E s.t. un En \ En 1
1
un 1 and dist(un , En 1 )
2
1
Then un um
if m n
2
Hence un contains no convergent subsequence.
Let
Theorem II.18
A : D( A) F
D ( A) E
closed linear operator with
then the following properties are equivalent
(i) R(A) is closed
(ii) R(A*) is closed
*
(iii)
R( A) N ( A )
(iv)
R( A ) N ( A)
*
Topological Complement
Let G be a closed vector subspace of
a Banach space E.
A vector subspace L of E is called
a topological complement of G if
(i)L is closed.
(ii)G∩L={0} and G+L=E
see
next
page
In this case, all
zE
can be expressed uniquely as z=x+y
with
x G, y L
It follows from Thm II.8 that the
projections z→x and z→y are linear
continuous and surjective.
Example for
Topological Complement
E: Banach space
G:finite dimensional subspace of E;
hence is closed.
Find a topological complement of G
see
next
page
Let e1 , e2 ,, en be a basis of G.
x G x 1 ( x )e1 n ( x )en
For i 1,, n
i : G R is linear continuous
i ( x ) i
G
x G
x
Since p( x ) i
G
x is sublinear,
by Hahn Banach Thm
i has an extension ˆi : E R s.t.
ˆi ( x ) i
G
x
xE
n
Let L ker ˆi .
i 1
Claim : L is a topo log ical complement of G.
Pf :
(1) Since ker ˆi is closed ,
n
L ker ˆi is closed .
i 1
( 2)To show that G L 0
If x G L , then
n
x i ( x )ei
, sin ce x G
i 1
n
n
i 1
i 1
ˆi ( x )ei 0 ei 0
Hence G L 0
n
, sin ce x L ker ˆi
i 1
(3) To show that E G L.
For any z E
n
let y ˆi ( z )ei G , then
i 1
n
z y z ˆi ( z )ei
i 1
For i0 1,, n
n
ˆi ( z y ) ˆi z ˆi ( z )ei
i 1
0
0
n
ˆi ( z ) ˆi ( z )ˆi ( ei )
0
i 1
ˆi ( z ) ˆi ( z ) 0
0
0
then z y L
z y ( x y) G L
Hence E G L
0
Remark
On finite dimensional vector space,
linear functional is continuous.
Prove in
next page
Let E be a vector space with dim E n.
Let e1 , e2 ,, en be a basis for E and
be a linear functional on E.
n
For x xi ei E
i 1
n
n
( x ) xi ei xi ei
i 1
i 1
( x)
n
xi ei
i 1
is bounded .
is continuous
12
2
xi
i 1
n
12
2
ei
i 1
n
Remark
Let E be a Banach space.
Let G be a closed v.s.s of E with
codimG < ∞, then
any algebraic complement is
topological complement of G
Typial example
in next page
Let
N E , dim N p
then
G x E f , x 0, f N
be a closed vector subspace of E and
codimG=p
Prove in
next page
證明很重要
Let
f1, f 2 ,, f p be
a basis for N .
Claim : there are e1 , e2 ,, e p E s.t.
f i , e j ij
1 i, j p
pf : Consider the map : E R p defined by
( x ) f1 , x ,, f p , x
xE
To show that is surjective
Suppose not , x0 R p \ ( E ) and
by Hahn Banach Thm ( Second Geometric Form)
we can find 1 , 2 ,, p 0 s.t.
( x ) x0
( x) 0
xE
xE
p
p
i 1
i 1
0 i fi , x i fi , x
xE
p
i fi 0
i 1
f1 ,, f p are linear dependent
Then e1 ,, e p E s.t.
( e1 ) 1,0,,0
( e2 ) 0,1,,0
( e p ) 0, ,,1
f i , e j ij
1 i, j p
e1 ,, e p are linear independent
the space generated by e1 ,, e p
is the topo log ical complement of G.
Lemma VI.6
(Fredholm Alternative)
Let E be a Banach space and T K ( E ) K ( E , E )
then (a) N(I-T) is of finite dimension
(b) R(I-T) is closed and more precisely
*
R( I T ) N ( I T )
(c)
N ( I T ) 0 R( I T ) E
(d)
dim N ( I T ) dim N ( I T )
*
(a ) Let E1 N ( I T ), then BE T ( BE )
1
Since T K ( E ), T ( BE ) is precompact
then BE is precompact
1
Thm VI .5 dim E1
(b) Suppose that f n un Tun I T un f as n
To show that f R( I T )
Since N ( I T ) is of finite dim ension,
there exist vn N ( I T ) such that
d n un vn dist(un , N ( I T ))
we have f n (un vn ) T (un vn )
Claim :
un vn is
( 4)
bounded .
[ Suppose the contrary. There is a subsequence
such that un vn
k
k
un v n
. Let wn
un v n
( 4) wn Twn 0
k
k
Extracting a subsequence ( still denoted by wn )
k
We may assume that Twn z
k
Then wn z and z N ( I T )
k
On the other hand ,
dist(un , N ( I T ) un vn
dist( wn , N ( I T )
1
un vn
un v n
In the lim it dist( z, N ( I T )) 1, which is absurb.]
un vn is bounded sequence.
Then there is a subsequence s.t. T un vn
( 4) un vn f . Put g f
k
k
then g Tg f i.e. f R ( I T )
Hence R ( I T ) is closed .
k
k
We have shown I T is of closed image.
We can apply Theorem II .18
*
R( I T ) N ( I T ) ;
R( I T ) N ( I T )
*
(c ) " "
Suppose the contrary. E1 R( I T ) E
Then E1 is a Banach space and T ( E1 ) E1
Since T is compact , T
E1
is compact
(b) ( I T ) E1 is a closed subspace of E1
Furthermore, ( I T ) E1 E1 because I T is injective.
Let E2 ( I T ) E1 , E3 ( I T ) E2 ,, En ( I T ) En 1 ,
Then E E1 E2 E3 , because I T is injective.
By Riesz Lemma , un En such that un 1 and
1
dist(un , En 1 )
2
For n m, En 1 En Em 1 Em
Tun Tum un Tun um Tum un um
Since un Tun um Tum un Em 1 ,
1
Tun Tum dist(um , Em 1 )
2
Then Tun contains no converging subsequence,
a contradiction.
R( I T ) E.
( c ) " "
Assume that R ( I T ) E
Then N ( I T * ) R ( I T ) 0, by Corollary II .17
Since T K ( E ), by Schauder Theorem T K ( E )
*
and then by previous proof we have R ( I T ) E
*
Again by Corollary II .17
N ( I T ) R( I T * ) 0.
( d ) Let d dim N ( I T ) and d * dim N ( I T * )
First to show that d * d
Suppose d d .
*
N ( I T ) admits a topo log y complement
and continuous projection P
from E onto N ( I T ).
*
R( I T ) N ( I T )
R ( I T ) has co dim d
*
and then admits
a topo log y complement F of dim ension d * .
a linear injection : N ( I T ) F .
Let S T P. Since T K ( E ) and
P is finite rank , S k ( E )
Claim : N ( I S ) 0
[0 u Su u Tu P u
u Tu 0 and P u 0
u N ( I T ) and then u 0
u 0]
( c ) R( I S ) E , which is impossible
because d d and so f F , f R( )
then the equation u Su f has no solution
Otherwise, u Su u Tu P u f F
then P u f
*
Apply this to T
*
dim N ( I T ) dim N ( I T ) dim N ( I T )
*
**
But N ( I T ) N ( I T )
**
T : E E ,
T : E E ) and E E
**
Hence dim N ( I T ) dim N ( I T )
*
Lemma VI.1 (Riesz-Lemma)
Let
For any
fixed , apply Green’s second
v
1( x, ) in the domain
u C , : C domain, bounded
\ B and then let 0 we have
identity to u2and
u
( x, )
u ( x, )udx ( x, )
u
ds
n x
n x