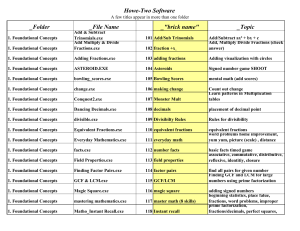
8 A list of all howe-two programs by sub menu with
... visualize and solve inequations emphasize structure needed to solve ax 206 Learn ax + b = cx + d + b = cx + d game for variety of linear equation in 207 linear matho one unknown (mental math) game(easy version) for variety of ...
... visualize and solve inequations emphasize structure needed to solve ax 206 Learn ax + b = cx + d + b = cx + d game for variety of linear equation in 207 linear matho one unknown (mental math) game(easy version) for variety of ...
Tensor Categories
... and Turaev, and many others. Initially, in many of these works tensor categories were merely a tool for solving various concrete problems, but gradually a general theory of tensor categories started to emerge, and by now there are many deep results about properties and classification of tensor catego ...
... and Turaev, and many others. Initially, in many of these works tensor categories were merely a tool for solving various concrete problems, but gradually a general theory of tensor categories started to emerge, and by now there are many deep results about properties and classification of tensor catego ...
Some Aspects of Harmonic Analysis on Commutative Topological
... the first separation condition, then one may say that X is regular in the strong sense, or that X satisfies the third separation condition. This implies that X is Hausdorff, because subsets of X with only one element are closed sets. If A is a commutative topological group, then A is regular as a to ...
... the first separation condition, then one may say that X is regular in the strong sense, or that X satisfies the third separation condition. This implies that X is Hausdorff, because subsets of X with only one element are closed sets. If A is a commutative topological group, then A is regular as a to ...
TANGENTS AND SECANTS OF ALGEBRAIC VARIETIES F. L. Zak
... X are reduced. In particular, if X is nonsingular and N < 2n, then all hyperplane sections of X are reduced. b) If a nondegenerate variety X n ⊂ PN has properties S3 and RN −n+2 (the last assumption means that N < 2n − b − 2), then all hyperplane sections of X are normal (and therefore irreducible a ...
... X are reduced. In particular, if X is nonsingular and N < 2n, then all hyperplane sections of X are reduced. b) If a nondegenerate variety X n ⊂ PN has properties S3 and RN −n+2 (the last assumption means that N < 2n − b − 2), then all hyperplane sections of X are normal (and therefore irreducible a ...
Multiplicative and Affine Poisson Structures on Lie Groups
... The Poisson bivector field π on a Poisson manifold P can also be regarded as a bundle map π # : T ∗ P → T P : (α, π # β) = π(α, β) (notice the sign convention here). For a smooth function f on P , the vector field Xf = π # (df ) is called the Hamiltonian vector field of f . When π is of maximal rank ...
... The Poisson bivector field π on a Poisson manifold P can also be regarded as a bundle map π # : T ∗ P → T P : (α, π # β) = π(α, β) (notice the sign convention here). For a smooth function f on P , the vector field Xf = π # (df ) is called the Hamiltonian vector field of f . When π is of maximal rank ...
Kazhdan`s Property (T)
... (iii) A lattice Γ in a locally compact group G has Property (T) if and only if G has it. Chapter 2 concentrates on a property which was shown in the late 70’s to be equivalent to Kazhdan’s property for a large class of groups: a topological group G has Property (FH) if any continuous action of G by ...
... (iii) A lattice Γ in a locally compact group G has Property (T) if and only if G has it. Chapter 2 concentrates on a property which was shown in the late 70’s to be equivalent to Kazhdan’s property for a large class of groups: a topological group G has Property (FH) if any continuous action of G by ...
Belmesnaoui Aqzzouz, Khalid Bouras WEAK AND ALMOST
... and conversely. To do this, we introduce a new property that we call the AM-compactness property of a Banach lattice. Also, we give some important consequences. More precisely, we will begin by characterizing Banach lattices on which the class of almost Dunford–Pettis operators coincides with that o ...
... and conversely. To do this, we introduce a new property that we call the AM-compactness property of a Banach lattice. Also, we give some important consequences. More precisely, we will begin by characterizing Banach lattices on which the class of almost Dunford–Pettis operators coincides with that o ...
LINEAR ALGEBRA
... xn = tn then (1) will be satisfied. By satisfied we mean that if we plug these numbers into the left side of (1) and do the arithmetic we will get b as an answer. The first thing to notice about the solution set to a single linear equation that contains at least two variables with non-zero coefficen ...
... xn = tn then (1) will be satisfied. By satisfied we mean that if we plug these numbers into the left side of (1) and do the arithmetic we will get b as an answer. The first thing to notice about the solution set to a single linear equation that contains at least two variables with non-zero coefficen ...
Linear Algebra - Cornell Computer Science
... x = 0, y = 8 x = −3, y = 2, x = −4, y = 0 x = 5, y = 18 Recall from our work above that there will be infinitely many solutions to a single linear equation. We’ll also leave it to you to verify that these four solutions are also four of the infinitely many solutions to the second equation in (4). Le ...
... x = 0, y = 8 x = −3, y = 2, x = −4, y = 0 x = 5, y = 18 Recall from our work above that there will be infinitely many solutions to a single linear equation. We’ll also leave it to you to verify that these four solutions are also four of the infinitely many solutions to the second equation in (4). Le ...
LINEAR ALGEBRA TEXTBOOK LINK
... integers, the collection of signed whole numbers such as 1,2,-4, and so on. This set, whose existence will be assumed, is denoted by Z. Other sets could be the set of people in a family or the set of donuts in a display case at the store. Sometimes parentheses, { } specify a set by listing the thing ...
... integers, the collection of signed whole numbers such as 1,2,-4, and so on. This set, whose existence will be assumed, is denoted by Z. Other sets could be the set of people in a family or the set of donuts in a display case at the store. Sometimes parentheses, { } specify a set by listing the thing ...
Trace of Positive Integer Power of Real 2 × 2 Matrices
... Traces of powers of matrices arise in several fields of mathematics, more specifically, Network Analysis, Numbertheory, Dynamical systems, Matrix theory, and Differential equations [1]. When analyzing a complex network, an important problem is to compute the total number of triangles of a connected ...
... Traces of powers of matrices arise in several fields of mathematics, more specifically, Network Analysis, Numbertheory, Dynamical systems, Matrix theory, and Differential equations [1]. When analyzing a complex network, an important problem is to compute the total number of triangles of a connected ...
Introductory Functional Analysis with Applications
... Functional analysis is an abstract branch of mathematics that originated from classical analysis. Its development started about eighty years ago, and nowadays functional analytic methods and results are important in various fields of mathematics and its applications. The impetus came from linear alg ...
... Functional analysis is an abstract branch of mathematics that originated from classical analysis. Its development started about eighty years ago, and nowadays functional analytic methods and results are important in various fields of mathematics and its applications. The impetus came from linear alg ...
Sheldon Axler Third Edition
... defined in this chapter as the sum of the eigenvalues and the product of the eigenvalues, both counting multiplicity. These easy-to-remember definitions would not be possible with the traditional approach to eigenvalues, because the traditional method uses determinants to prove that sufficient eigenval ...
... defined in this chapter as the sum of the eigenvalues and the product of the eigenvalues, both counting multiplicity. These easy-to-remember definitions would not be possible with the traditional approach to eigenvalues, because the traditional method uses determinants to prove that sufficient eigenval ...
linked PDF version! - Math-UMN
... The main novelty is that most of the standard exercises in abstract algebra are given here as worked examples. Some additional exercises are given, which are variations on the worked examples. The reader might contemplate the examples before reading the solutions, but this is not mandatory. The exam ...
... The main novelty is that most of the standard exercises in abstract algebra are given here as worked examples. Some additional exercises are given, which are variations on the worked examples. The reader might contemplate the examples before reading the solutions, but this is not mandatory. The exam ...
Coxeter groups
... reduced. Multiplication on F(A) is given by concatenation followed by removal of all forbidden occurrences so as to obtain a reduced word, and in which the empty word 1 is the identity element. The fact that F(A) is a group requires a proof. This proof will be postponed till Lecture 2; it hinges on ...
... reduced. Multiplication on F(A) is given by concatenation followed by removal of all forbidden occurrences so as to obtain a reduced word, and in which the empty word 1 is the identity element. The fact that F(A) is a group requires a proof. This proof will be postponed till Lecture 2; it hinges on ...
REPRESENTATION THEORY Tammo tom Dieck
... with the properties v(hg) = (vh)g and ve = v, and K-linear right translations rg : v 7→ vg. These will be called right representations as opposed to left representations defined above. The map rg : v 7→ vg is then the right translation by g. Note that now rg ◦ rh = rhg (contravariance). If V is a ri ...
... with the properties v(hg) = (vh)g and ve = v, and K-linear right translations rg : v 7→ vg. These will be called right representations as opposed to left representations defined above. The map rg : v 7→ vg is then the right translation by g. Note that now rg ◦ rh = rhg (contravariance). If V is a ri ...
M08/18
... Assume that n > 1. Let Bx , By be the complemented cyclic subgroups B obtained by Lemma 3.3 for x, y, respectively. Then |Bx | = |By | since A/hxi ∼ = A/hyi, and hence the integer ej determined by Lemma 3.3 is the same for x and y. We can in fact assume that already j is the same. Furthermore, we ca ...
... Assume that n > 1. Let Bx , By be the complemented cyclic subgroups B obtained by Lemma 3.3 for x, y, respectively. Then |Bx | = |By | since A/hxi ∼ = A/hyi, and hence the integer ej determined by Lemma 3.3 is the same for x and y. We can in fact assume that already j is the same. Furthermore, we ca ...
14 - science.uu.nl project csg
... of the group, a closely related lifting theorem by Casselman was used by Arthur in the proof of the Paley-Wiener theorem, see [1], Thm. II.4.1. However, no proof has yet appeared of Casselman’s theorem. The tools developed in this paper are used in [11], and they will also be applied in forthcoming ...
... of the group, a closely related lifting theorem by Casselman was used by Arthur in the proof of the Paley-Wiener theorem, see [1], Thm. II.4.1. However, no proof has yet appeared of Casselman’s theorem. The tools developed in this paper are used in [11], and they will also be applied in forthcoming ...
2010 Edition - Abstract Algebra: Theory and Applications
... abstract algebra. Traditionally, these courses have covered the theoretical aspects of groups, rings, and fields. However, with the development of computing in the last several decades, applications that involve abstract algebra and discrete mathematics have become increasingly important, and many s ...
... abstract algebra. Traditionally, these courses have covered the theoretical aspects of groups, rings, and fields. However, with the development of computing in the last several decades, applications that involve abstract algebra and discrete mathematics have become increasingly important, and many s ...
2009 Edition - Abstract Algebra: Theory and Applications
... abstract algebra. Traditionally, these courses have covered the theoretical aspects of groups, rings, and fields. However, with the development of computing in the last several decades, applications that involve abstract algebra and discrete mathematics have become increasingly important, and many s ...
... abstract algebra. Traditionally, these courses have covered the theoretical aspects of groups, rings, and fields. However, with the development of computing in the last several decades, applications that involve abstract algebra and discrete mathematics have become increasingly important, and many s ...
Abstract Algebra Theory and Applications
... This text is intended for a one- or two-semester undergraduate course in abstract algebra. Traditionally, these courses have covered the theoretical aspects of groups, rings, and fields. However, with the development of computing in the last several decades, applications that involve abstract algebr ...
... This text is intended for a one- or two-semester undergraduate course in abstract algebra. Traditionally, these courses have covered the theoretical aspects of groups, rings, and fields. However, with the development of computing in the last several decades, applications that involve abstract algebr ...
Ideal perturbation of elements in C*-algebras by Wha-Suck Lee
... where we embed a C*-algebra as a closed 2-sided ideal of another C*-algebra which lacks an identity. This embedding gives us licence to treat any C*-algebra as a C*-algebra without an identity for our purposes. This of fundamental importance in the thesis : it is an appropriate first theme. The seco ...
... where we embed a C*-algebra as a closed 2-sided ideal of another C*-algebra which lacks an identity. This embedding gives us licence to treat any C*-algebra as a C*-algebra without an identity for our purposes. This of fundamental importance in the thesis : it is an appropriate first theme. The seco ...
2015 Edition - Abstract Algebra: Theory and Applications
... involve abstract algebra and discrete mathematics have become increasingly important, and many science, engineering, and computer science students are now electing to minor in mathematics. Though theory still occupies a central role in the subject of abstract algebra and no student should go through ...
... involve abstract algebra and discrete mathematics have become increasingly important, and many science, engineering, and computer science students are now electing to minor in mathematics. Though theory still occupies a central role in the subject of abstract algebra and no student should go through ...
Undergraduate Texts in Mathematics
... • The part of the theory of polynomials that will be needed to understand linear operators is presented in Chapter 4. If you take class time going through the proofs in this chapter (which contains no linear algebra), then you probably will not have time to cover some important aspects of linear alg ...
... • The part of the theory of polynomials that will be needed to understand linear operators is presented in Chapter 4. If you take class time going through the proofs in this chapter (which contains no linear algebra), then you probably will not have time to cover some important aspects of linear alg ...
An Introductory Approach (Universitext)
... NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use i ...
... NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use i ...























