Download Lecture 05

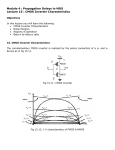
EE466: VLSI Design
Lecture 05: DC and transient response –
CMOS Inverters
4: DC and Transient Response
CMOS VLSI Design
Slide 1
Outline




DC Response
Logic Levels and Noise Margins
Transient Response
Delay Estimation
4: DC and Transient Response
CMOS VLSI Design
Slide 2
Activity
1) If the width of a transistor increases, the current will
increase
decrease
not change
2) If the length of a transistor increases, the current will
increase
decrease
not change
3) If the supply voltage of a chip increases, the maximum
transistor current will
increase
decrease
not change
4) If the width of a transistor increases, its gate capacitance will
increase
decrease
not change
5) If the length of a transistor increases, its gate capacitance will
increase
decrease
not change
6) If the supply voltage of a chip increases, the gate capacitance
of each transistor will
increase
decrease
not change
4: DC and Transient Response
CMOS VLSI Design
Slide 3
Activity
1) If the width of a transistor increases, the current will
increase
decrease
not change
2) If the length of a transistor increases, the current will
increase
decrease
not change
3) If the supply voltage of a chip increases, the maximum
transistor current will
increase
decrease
not change
4) If the width of a transistor increases, its gate capacitance will
increase
decrease
not change
5) If the length of a transistor increases, its gate capacitance will
increase
decrease
not change
6) If the supply voltage of a chip increases, the gate capacitance
of each transistor will
increase
decrease
not change
4: DC and Transient Response
CMOS VLSI Design
Slide 4
DC Response
 DC Response: Vout vs. Vin for a gate
 Ex: Inverter
– When Vin = 0
->
Vout = VDD
– When Vin = VDD
->
Vout = 0
VDD
– In between, Vout depends on
Idsp
transistor size and current
Vin
Vout
– By KCL, must settle such that
Idsn
Idsn = |Idsp|
– We could solve equations
– But graphical solution gives more insight
4: DC and Transient Response
CMOS VLSI Design
Slide 5
Transistor Operation
 Current depends on region of transistor behavior
 For what Vin and Vout are nMOS and pMOS in
– Cutoff?
– Linear?
– Saturation?
4: DC and Transient Response
CMOS VLSI Design
Slide 6
nMOS Operation
Cutoff
Linear
Saturated
Vgsn <
Vgsn >
Vgsn >
Vdsn <
Vdsn >
VDD
Vin
Idsp
Vout
Idsn
4: DC and Transient Response
CMOS VLSI Design
Slide 7
nMOS Operation
Cutoff
Linear
Saturated
Vgsn < Vtn
Vgsn > Vtn
Vgsn > Vtn
Vdsn < Vgsn – Vtn
Vdsn > Vgsn – Vtn
VDD
Vin
Idsp
Vout
Idsn
4: DC and Transient Response
CMOS VLSI Design
Slide 8
nMOS Operation
Cutoff
Linear
Saturated
Vgsn < Vtn
Vgsn > Vtn
Vgsn > Vtn
Vdsn < Vgsn – Vtn
Vdsn > Vgsn – Vtn
VDD
Vgsn = Vin
Vin
Vdsn = Vout
4: DC and Transient Response
Idsp
Vout
Idsn
CMOS VLSI Design
Slide 9
nMOS Operation
Cutoff
Linear
Saturated
Vgsn < Vtn
Vin < Vtn
Vgsn > Vtn
Vin > Vtn
Vdsn < Vgsn – Vtn
Vout < Vin - Vtn
Vgsn > Vtn
Vin > Vtn
Vdsn > Vgsn – Vtn
Vout > Vin - Vtn
VDD
Vgsn = Vin
Vin
Vdsn = Vout
4: DC and Transient Response
Idsp
Vout
Idsn
CMOS VLSI Design
Slide 10
pMOS Operation
Cutoff
Linear
Saturated
Vgsp >
Vgsp <
Vgsp <
Vdsp >
Vdsp <
VDD
Vin
Idsp
Vout
Idsn
4: DC and Transient Response
CMOS VLSI Design
Slide 11
pMOS Operation
Cutoff
Linear
Saturated
Vgsp > Vtp
Vgsp < Vtp
Vgsp < Vtp
Vdsp > Vgsp – Vtp
Vdsp < Vgsp – Vtp
VDD
Vin
Idsp
Vout
Idsn
4: DC and Transient Response
CMOS VLSI Design
Slide 12
pMOS Operation
Cutoff
Linear
Saturated
Vgsp > Vtp
Vgsp < Vtp
Vgsp < Vtp
Vdsp > Vgsp – Vtp
Vdsp < Vgsp – Vtp
VDD
Vgsp = Vin - VDD
Vtp < 0
Vin
Vdsp = Vout - VDD
4: DC and Transient Response
Idsp
Vout
Idsn
CMOS VLSI Design
Slide 13
pMOS Operation
Cutoff
Linear
Saturated
Vgsp > Vtp
Vin > VDD + Vtp
Vgsp < Vtp
Vin < VDD + Vtp
Vdsp > Vgsp – Vtp
Vout > Vin - Vtp
Vgsp < Vtp
Vin < VDD + Vtp
Vdsp < Vgsp – Vtp
Vout < Vin - Vtp
VDD
Vgsp = Vin - VDD
Vtp < 0
Vin
Vdsp = Vout - VDD
4: DC and Transient Response
Idsp
Vout
Idsn
CMOS VLSI Design
Slide 14
I-V Characteristics
 Make pMOS is wider than nMOS such that bn = bp
Vgsn5
Vgsn4
Idsn
Vgsn3
-Vdsp
Vgsp1
Vgsp2
-VDD
0
VDD
Vdsn
Vgsp3
Vgsp4
Vgsn2
Vgsn1
-Idsp
Vgsp5
4: DC and Transient Response
CMOS VLSI Design
Slide 15
Current vs. Vout, Vin
Idsn, |Idsp|
Vin0
Vin5
Vin1
Vin4
Vin2
Vin3
Vin3
Vin4
Vin2
Vin1
Vout
4: DC and Transient Response
CMOS VLSI Design
VDD
Slide 16
Load Line Analysis
 For a given Vin:
– Plot Idsn, Idsp vs. Vout
– Vout must be where |currents| are equal in
Idsn, |Idsp|
Vin0
Vin5
Vin1
Vin4
Vin2
Vin3
Vin3
Vin4
Vin2
Vin1
Vout
4: DC and Transient Response
CMOS VLSI Design
VDD
Vin
Idsp
Vout
Idsn
VDD
Slide 17
Load Line Analysis
 Vin = 0
Vin0
Idsn, |Idsp|
Vin0
Vout
4: DC and Transient Response
CMOS VLSI Design
VDD
Slide 18
Load Line Analysis
 Vin = 0.2VDD
Idsn, |Idsp|
Vin1
Vin1
Vout
4: DC and Transient Response
CMOS VLSI Design
VDD
Slide 19
Load Line Analysis
 Vin = 0.4VDD
Idsn, |Idsp|
Vin2
Vin2
Vout
4: DC and Transient Response
CMOS VLSI Design
VDD
Slide 20
Load Line Analysis
 Vin = 0.6VDD
Idsn, |Idsp|
Vin3
Vin3
Vout
4: DC and Transient Response
CMOS VLSI Design
VDD
Slide 21
Load Line Analysis
 Vin = 0.8VDD
Vin4
Idsn, |Idsp|
Vin4
Vout
4: DC and Transient Response
CMOS VLSI Design
VDD
Slide 22
Load Line Analysis
 Vin = VDD
Vin0
Idsn, |Idsp|
Vin5
Vin1
Vin2
Vin3
Vin4
Vout
4: DC and Transient Response
CMOS VLSI Design
VDD
Slide 23
Load Line Summary
Idsn, |Idsp|
Vin0
Vin5
Vin1
Vin4
Vin2
Vin3
Vin3
Vin4
Vin2
Vin1
Vout
4: DC and Transient Response
CMOS VLSI Design
VDD
Slide 24
DC Transfer Curve
 Transcribe points onto Vin vs. Vout plot
Vin0
Vin5
Vin1
Vin4
Vin2
Vin3
Vin3
Vin4
Vin2
Vin1
Vout
4: DC and Transient Response
VDD
A
B
Vout
VDD
C
D
0
Vtn
VDD/2
E
VDD+Vtp
VDD
Vin
CMOS VLSI Design
Slide 25
Operating Regions
 Revisit transistor operating regions
Region
nMOS
VDD
pMOS
A
A
B
B
Vout
C
C
D
D
0
E
Vtn
VDD/2
E
VDD+Vtp
VDD
Vin
4: DC and Transient Response
CMOS VLSI Design
Slide 26
Operating Regions
 Revisit transistor operating regions
Region
nMOS
A
Cutoff
Linear
B
Saturation
Linear
C
Saturation
Saturation
D
Linear
Saturation
E
Linear
VDD
pMOS
A
B
Vout
Cutoff
C
D
0
Vtn
VDD/2
E
VDD+Vtp
VDD
Vin
4: DC and Transient Response
CMOS VLSI Design
Slide 27
Beta Ratio
 If bp / bn  1, switching point will move from VDD/2
 Called skewed gate
 Other gates: collapse into equivalent inverter
VDD
bp
 10
bn
Vout
2
1
0.5
bp
 0.1
bn
0
Vin
4: DC and Transient Response
CMOS VLSI Design
VDD
Slide 28
Noise Margins
 How much noise can a gate input see before it does
not recognize the input?
Output Characteristics
Logical High
Output Range
VDD
Input Characteristics
Logical High
Input Range
VOH
NMH
VIH
VIL
Indeterminate
Region
NML
Logical Low
Output Range
VOL
Logical Low
Input Range
GND
4: DC and Transient Response
CMOS VLSI Design
Slide 29
Logic Levels
 To maximize noise margins, select logic levels at
Vout
VDD
b p/b n > 1
Vin
Vout
Vin
0
VDD
4: DC and Transient Response
CMOS VLSI Design
Slide 30
Logic Levels
 To maximize noise margins, select logic levels at
– unity gain point of DC transfer characteristic
Vout
Unity Gain Points
Slope = -1
VDD
VOH
b p/b n > 1
Vin
VOL
Vout
Vin
0
Vtn
4: DC and Transient Response
VIL VIH VDD- VDD
|Vtp|
CMOS VLSI Design
Slide 31
Transient Response
 DC analysis tells us Vout if Vin is constant
 Transient analysis tells us Vout(t) if Vin(t) changes
– Requires solving differential equations
 Input is usually considered to be a step or ramp
– From 0 to VDD or vice versa
4: DC and Transient Response
CMOS VLSI Design
Slide 32
Inverter Step Response
 Ex: find step response of inverter driving load cap
Vin (t ) 
Vin(t)
Vout (t  t0 ) 
dVout (t )

dt
4: DC and Transient Response
Vout(t)
Cload
Idsn(t)
CMOS VLSI Design
Slide 33
Inverter Step Response
 Ex: find step response of inverter driving load cap
Vin (t )  u(t  t0 )VDD
Vin(t)
Vout (t  t0 ) 
dVout (t )

dt
4: DC and Transient Response
Vout(t)
Cload
Idsn(t)
CMOS VLSI Design
Slide 34
Inverter Step Response
 Ex: find step response of inverter driving load cap
Vin (t )  u(t  t0 )VDD
Vin(t)
Vout (t  t0 )  VDD
dVout (t )

dt
4: DC and Transient Response
Vout(t)
Cload
Idsn(t)
CMOS VLSI Design
Slide 35
Inverter Step Response
 Ex: find step response of inverter driving load cap
Vin (t )  u(t  t0 )VDD
Vin(t)
Vout (t  t0 )  VDD
dVout (t )
I dsn (t )

dt
Cload


I dsn (t )  


Vout
Vout
Vout(t)
Cload
Idsn(t)
t  t0
 VDD  Vt
 VDD  Vt
4: DC and Transient Response
CMOS VLSI Design
Slide 36
Inverter Step Response
 Ex: find step response of inverter driving load cap
Vin (t )  u(t  t0 )VDD
Vin(t)
Vout (t  t0 )  VDD
dVout (t )
I dsn (t )

dt
Cload
Vout(t)
Cload
Idsn(t)

0


2
b
I dsn (t )  
V

V


DD
2

V (t )
 b VDD  Vt  out 2
 
 V (t ) V  V  V
 out
out
DD
t

4: DC and Transient Response
CMOS VLSI Design
t  t0
Vout  VDD  Vt
Slide 37
Inverter Step Response
 Ex: find step response of inverter driving load cap
Vin (t )  u(t  t0 )VDD
Vin(t)
Vout (t  t0 )  VDD
Vout(t)
Cload
dVout (t )
I dsn (t )

dt
Cload
Idsn(t)
Vin(t)

0


2
b
I dsn (t )  
V

V


DD
2

V (t )
 b VDD  Vt  out 2
 
 V (t ) V  V  V
 out
out
DD
t

4: DC and Transient Response
CMOS VLSI Design
t  t0
Vout  VDD  Vt
Vout(t)
t0
t
Slide 38
Delay Definitions
 tpdr:
 tpdf:
 tpd:
 t r:
 tf: fall time
4: DC and Transient Response
CMOS VLSI Design
Slide 39
Delay Definitions
 tpdr: rising propagation delay
– From input to rising output crossing VDD/2
 tpdf: falling propagation delay
– From input to falling output crossing VDD/2
 tpd: average propagation delay
– tpd = (tpdr + tpdf)/2
 tr: rise time
– From output crossing 0.2 VDD to 0.8 VDD
 tf: fall time
– From output crossing 0.8 VDD to 0.2 VDD
4: DC and Transient Response
CMOS VLSI Design
Slide 40
Delay Definitions
 tcdr: rising contamination delay
– From input to rising output crossing VDD/2
 tcdf: falling contamination delay
– From input to falling output crossing VDD/2
 tcd: average contamination delay
– tpd = (tcdr + tcdf)/2
4: DC and Transient Response
CMOS VLSI Design
Slide 41
Simulated Inverter Delay
 Solving differential equations by hand is too hard
 SPICE simulator solves the equations numerically
– Uses more accurate I-V models too!
 But simulations take time to write
2.0
1.5
1.0
(V)
Vin
tpdf = 66ps
tpdr = 83ps
Vout
0.5
0.0
0.0
200p
400p
600p
800p
1n
t(s)
4: DC and Transient Response
CMOS VLSI Design
Slide 42
Delay Estimation
 We would like to be able to easily estimate delay
– Not as accurate as simulation
– But easier to ask “What if?”
 The step response usually looks like a 1st order RC
response with a decaying exponential.
 Use RC delay models to estimate delay
– C = total capacitance on output node
– Use effective resistance R
– So that tpd = RC
 Characterize transistors by finding their effective R
– Depends on average current as gate switches
4: DC and Transient Response
CMOS VLSI Design
Slide 43
Effective Resistance
 Shockley models have limited value
– Not accurate enough for modern transistors
– Too complicated for much hand analysis
 Simplification: treat transistor as resistor
– Replace Ids(Vds, Vgs) with effective resistance R
• Ids = Vds/R
– R averaged across switching of digital gate
 Too inaccurate to predict current at any given time
– But good enough to predict RC delay
4: DC and Transient Response
CMOS VLSI Design
Slide 44
RC Delay Model
 Use equivalent circuits for MOS transistors
– Ideal switch + capacitance and ON resistance
– Unit nMOS has resistance R, capacitance C
– Unit pMOS has resistance 2R, capacitance C
 Capacitance proportional to width
 Resistance inversely proportional to width
d
g
d
k
s
s
kC
R/k
kC
2R/k
g
g
kC
kC
s
4: DC and Transient Response
d
k
s
kC
g
kC
d
CMOS VLSI Design
Slide 45
RC Values
 Capacitance
– C = Cg = Cs = Cd = 2 fF/mm of gate width
– Values similar across many processes
 Resistance
– R  6 KW*mm in 0.6um process
– Improves with shorter channel lengths
 Unit transistors
– May refer to minimum contacted device (4/2 l)
– Or maybe 1 mm wide device
– Doesn’t matter as long as you are consistent
4: DC and Transient Response
CMOS VLSI Design
Slide 46
Inverter Delay Estimate
 Estimate the delay of a fanout-of-1 inverter
A
2 Y
2
1
1
4: DC and Transient Response
CMOS VLSI Design
Slide 47
Inverter Delay Estimate
 Estimate the delay of a fanout-of-1 inverter
2C
R
A
2 Y
2
1
1
2C
2C
Y
R
C
C
C
4: DC and Transient Response
CMOS VLSI Design
Slide 48
Inverter Delay Estimate
 Estimate the delay of a fanout-of-1 inverter
2C
R
A
2 Y
2
1
1
2C
2C
2C
2C
Y
R
C
R
C
C
C
C
4: DC and Transient Response
CMOS VLSI Design
Slide 49
Inverter Delay Estimate
 Estimate the delay of a fanout-of-1 inverter
2C
R
A
2 Y
2
1
1
2C
2C
2C
2C
Y
R
C
R
C
C
C
C
d = 6RC
4: DC and Transient Response
CMOS VLSI Design
Slide 50
Example: 3-input NAND
 Sketch a 3-input NAND with transistor widths
chosen to achieve effective rise and fall resistances
equal to a unit inverter (R).
4: DC and Transient Response
CMOS VLSI Design
Slide 51
Example: 3-input NAND
 Sketch a 3-input NAND with transistor widths
chosen to achieve effective rise and fall resistances
equal to a unit inverter (R).
4: DC and Transient Response
CMOS VLSI Design
Slide 52
Example: 3-input NAND
 Sketch a 3-input NAND with transistor widths
chosen to achieve effective rise and fall resistances
equal to a unit inverter (R).
2
2
2
3
3
3
4: DC and Transient Response
CMOS VLSI Design
Slide 53
3-input NAND Caps
 Annotate the 3-input NAND gate with gate and
diffusion capacitance.
2
2
2
3
3
3
4: DC and Transient Response
CMOS VLSI Design
Slide 54
3-input NAND Caps
 Annotate the 3-input NAND gate with gate and
diffusion capacitance.
2C
2
2C
2C
2C
2
2C
2C
2C
3C
3C
3C
4: DC and Transient Response
2
CMOS VLSI Design
2C
2C
3
3
3
3C
3C
3C
3C
Slide 55
3-input NAND Caps
 Annotate the 3-input NAND gate with gate and
diffusion capacitance.
2
2
2
3
5C
3
5C
3
5C
4: DC and Transient Response
CMOS VLSI Design
9C
3C
3C
Slide 56
Elmore Delay
 ON transistors look like resistors
 Pullup or pulldown network modeled as RC ladder
 Elmore delay of RC ladder
t pd 

Ri to sourceCi
nodes i
 R1C1   R1  R2  C2  ...   R1  R2  ...  RN  CN
R1
R2
R3
C1
C2
4: DC and Transient Response
RN
C3
CMOS VLSI Design
CN
Slide 57
Example: 2-input NAND
 Estimate worst-case rising and falling delay of 2input NAND driving h identical gates.
2
2
A
2
B
2x
4: DC and Transient Response
Y
h copies
CMOS VLSI Design
Slide 58
Example: 2-input NAND
 Estimate rising and falling propagation delays of a 2input NAND driving h identical gates.
2
2
A
2
B
2x
Y
4hC
6C
4: DC and Transient Response
h copies
2C
CMOS VLSI Design
Slide 59
Example: 2-input NAND
 Estimate rising and falling propagation delays of a 2input NAND driving h identical gates.
2
2
A
2
B
2x
R
Y
(6+4h)C
Y
4hC
6C
h copies
2C
t pdr 
4: DC and Transient Response
CMOS VLSI Design
Slide 60
Example: 2-input NAND
 Estimate rising and falling propagation delays of a 2input NAND driving h identical gates.
2
2
A
2
B
2x
R
Y
(6+4h)C
Y
4hC
6C
h copies
2C
t pdr  6  4h  RC
4: DC and Transient Response
CMOS VLSI Design
Slide 61
Example: 2-input NAND
 Estimate rising and falling propagation delays of a 2input NAND driving h identical gates.
2
2
A
2
B
2x
Y
4hC
6C
4: DC and Transient Response
h copies
2C
CMOS VLSI Design
Slide 62
Example: 2-input NAND
 Estimate rising and falling propagation delays of a 2input NAND driving h identical gates.
2
2
A
2
B
2x
x
R/2
R/2
2C
Y
4hC
6C
Y
(6+4h)C
4: DC and Transient Response
h copies
2C
t pdf 
CMOS VLSI Design
Slide 63
Example: 2-input NAND
 Estimate rising and falling propagation delays of a 2input NAND driving h identical gates.
2
2
A
2
B
2x
x
R/2
R/2
2C
Y
(6+4h)C
Y
4hC
6C
h copies
2C
t pdf   2C   R2    6  4h  C   R2  R2 
4: DC and Transient Response
  7  4h  RC
CMOS VLSI Design
Slide 64
Delay Components
 Delay has two parts
– Parasitic delay
• 6 or 7 RC
• Independent of load
– Effort delay
• 4h RC
• Proportional to load capacitance
4: DC and Transient Response
CMOS VLSI Design
Slide 65
Contamination Delay
 Best-case (contamination) delay can be substantially
less than propagation delay.
 Ex: If both inputs fall simultaneously
2
2
A
2
B
2x
R R
Y
(6+4h)C
Y
4hC
6C
2C
tcdr   3  2h  RC
4: DC and Transient Response
CMOS VLSI Design
Slide 66
Diffusion Capacitance
 we assumed contacted diffusion on every s / d.
 Good layout minimizes diffusion area
 Ex: NAND3 layout shares one diffusion contact
– Reduces output capacitance by 2C
– Merged uncontacted diffusion might help too
2C
2C
Shared
Contacted
Diffusion
Isolated
Contacted
Diffusion
Merged
Uncontacted
Diffusion
2
2
2
3
3
3C 3C 3C
4: DC and Transient Response
CMOS VLSI Design
3
7C
3C
3C
Slide 67
Layout Comparison
 Which layout is better?
VDD
A
VDD
B
Y
GND
4: DC and Transient Response
A
B
Y
GND
CMOS VLSI Design
Slide 68