Download Solutions to Problems for Chapter One ( ) 0.0254 m ( ( ( ).

Solutions to Problems for Chapter One
1-1) The SI unit for length is the meter. The English unit for length is the foot. A measurement
of length in one of these systems can be transformed to the other by using the following
equivalence:
1in ≡ 2.54 cm ≡ 0.0254 m (exact) .
In the United States of America, by convention, the English System is still used by many people.
This problem is designed to help you gain some felicity in moving seamlessly between the two
systems. Use the equivalence given above, to find the following:
a)
b)
c)
d)
e)
a)
b)
c)
d)
1mile ≡
1×10 3 m ≡
1mph ≡
1 km / hr ≡
92,957 ,130 miles ≡
meters .
mile .
m/s.
mph .
m,
this last value is the average distance between the center of the Earth and the center of
the Sun. It is called an astronomical unit. It is the “meter” stick for the solar system.
1 mile ≡ 5,280 ft ≡ 5,280 (12 in ) ≡ 5,280 (12 ) (0.0254 m ) ≡ 1,609.344 m .
⎛ mile ⎞
1 km ≡ 1× 10 3 m ≡ 1× 10 3 ⎜
≡ 0.6214 mile .
⎝ 1,609.344 ⎟⎠
mile 1,609 , 344 m
1
≡
≡ 0.4470 m / s .
hr
3, 600 s
km 0.6214 mile
1 ≡
.
hr
hr
92,957 ,130 miles ≡ 92,957,130 (1,609.344 m ) ≡ 1.496 × 1011 m .
e)
1-2) The SI unit for mass is the kilogram. A pharmaceutical company manufacture one hundred
million pills of a specific medicine called cure-all. The dosage required in each pill is fifty
milligrams. In the manufacturing process, one per cent of the product is contaminated and must be
discarded. Calculate how much cure-all, in kilograms, is produced annually.
Recall that
1kg ≡ 1,000 grams .
The total mass needed is given by
(
)
(
)(
)
m = N pills m per pill = 100 × 10 6 ⎡⎣ 50 10 −3 10−3 kg ⎤⎦ = 5,000 kg .
Of this, of course, only ninety-nine per cent made it to the consumer;
msold = 0.99m = 4, 950 kg .
1-3) The SI unit for temporal duration is the second. Calculate the number of seconds that pass in
the following time intervals:
a) One hour.
b) One day.
c) One week.
d) One month (30 days) .
e) One year.
f)
Eighty years.
S 1-1
g)
h)
i)
One millennium.
Five billion years.
Fifteen billion years.
1 hr ≡ 60 min ≡ 60 ( 60 s ) ≡ 3,600 s .
1 mean solar day ≡ 24 hr ≡ 24 ( 3,600 s ) ≡ 8.640 × 104 s .
a)
b)
(
)
1 week ≡ 7 days ≡ 7 8.640 × 10 4 s ≡ 6.048 × 105 s .
c)
(
)
1 month ≡ 30 days ≡ 30 8.640 × 10 4 s ≡ 2.592 ×10 6 s .
d)
(
)
1 mean solar year ≡ 365 days ≡ 365 8.640 × 10 4 s ≡ 3.1536 × 107 s .
e)
(This value is nicely approximated by π ×10 s .)
7
(
)
80 years ≡ 80 3.1536 ×10 7 s ≡ 2.523 × 109 s .
f)
(
)
g)
1 millennium ≡ 1, 000 years ≡ 1,000 3.1536 ×10 7 s ≡ 3.1536 × 1010 s .
h)
5 billion years ≡ 5 × 10 9 3.1536 ×10 7 s = 1.5768 × 1017 s .
(
)
(
)
i)
15 billion years ≡ 15 × 10 3.1536 ×10 s = 4.7304 ×10 s .
1-4) The meter is the SI standard unit of length. In this exercise, we want you to get some sense
of the range of lengths that are found in the universe.
−17
a.) The radius of an electron is approximately Re = 1.0 ×10
m.
Calculate the approximate volume of the electron. (The size of the
electron is very difficult to measure. It really does act as if it were a point mass.)
9
7
(
Ve = ( 4 / 3)π Re3 = (4 / 3) π 1.0 × 10−17 m
b)
)
3
17
= 4.19 ×10 −51 m 3 .
The most abundant element in the visible universe is hydrogen. We model this
atom as monatomic and composed of one proton and one electron. The nucleus can be
−15
approximated as a sphere of radius R p = 1.0 × 10 m , while the entire atom is
−10
modeled as a sphere of radius RH = 0.50 ×10
m . Calculate the ratio of the
volume of the hydrogen atom to the volume of the electron.
V H ( 4 / 3)π R 3H ⎛ 0.50 × 10 −10 m ⎞
=
= 1.25 ×10 20 .
3 = ⎜
−17
⎟
Ve ( 4 / 3) π Re ⎝ 1.0 ×10 m ⎠
3
Calculate the ratio of the volume of hydrogen atom to the volume of the proton.
V H ( 4 / 3)π R 3H ⎛ 0.50 × 10 −10 m ⎞
=
= 1.25 ×1014
3 = ⎜
−15
⎟
Vp ( 4 / 3)π R p ⎝ 1.0 ×10 m ⎠
3
c)
The cross-sectional area of the electron is, approximately,
(
Acs ,e = π R e2 = π 1 ×10 −17 m
)
2
= π × 10−34 m 2 ,
the cross-sectional area of the proton is, approximately,
(
Acs ,p = π R 2p = π 1 × 10−15 m
S 1-2
)
2
= π × 10 −30 m 2 ,
and the cross-sectional area of the hydrogen atom is, approximately,
(
Acs ,H = π R H = π 0.5 × 10
2
−10
m
)
2
=
π
−20
2
×10 m .
4
The ratio of the sum of the cross-sectional area of the electron and the proton to that of
the entire cross-sectional area of the atom is , approximately,
(
) (
2
1 × 10−17 m + 1× 10 −15 m
Acs ,e + Acs ,p π Re2 + π R 2p
=
=
2
Acs ,H
π RH2
0.5 × 10−10 m
d)
(
)
)
2
= 4 ×10 −10
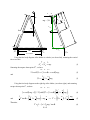
Suppose we launch an electrically neutral object with the same dimensions as an
electron toward a hydrogen atom like the one pictured below. If this object is just as
likely to strike at any point inside the atom, calculate a reasonable estimate of the
probability that there will be a collision. Calculate a reasonable estimate of the
probability that this object will pass on through without a collision. Assume the object
must pass through the boundary of the atom.
Model of A Monatomic Hydrogen Atom
Atom as Target
R1 = 3Re
e−
RH
e−
p
p
R2 = R p + 2Re
The neutral object will collide with the electron if it gets within a circle centered on the
electron of radius R1 . It will collide with the proton if it gets within a circle centered on the proton
of radius R2 . The ratio of the sum of the areas of the circles to that of the whole atom would
represent a reasonable estimate of the probability of a collision. If the neutral object is restricted to
area within the atom, then if is also reasonable to suggest it will “see” only approximately half of
the circle around the electron. So, we have
Pcollision =
2
(1 / 2 )π R12 + π R22 (1 / 2 ) (3Re ) + ( Rp + 2Re )
π RH2
(1 / 2) ( 3 ×10 −17 )
2
=
=
(
+ 10−15 + 2 ×10 −17
(0.5 × 10 )
−10 2
S 1-3
)
R 2H
2
= 4.2 ×10 −10 .
2
The probability, then, of no collision is given by
Pno collision = 1 − Pcollision = 0.99999999958 .
I recall an elementary particle physicist once describing the collision of elementary particles in an
accelerator like two people shooting bullets at each other while standing on the opposite borders of
the greaaaaat state of Texas and expecting the bullets to collide.
8
1-5.) The Sun has a mean radius of R = 6.96 ×10 m , while the mean radius of the Earth is
R⊕ = 6.371 × 10 6 m . On average, the distance from the center of the Earth to the center of the
11
Sun is r⊕ = 1.496 × 10 m ; called an astronomical unit. The speed of light in vacuum is one
of the most accurately measured quantities in physics. Its exact value, to nine significant digits is
c = 2.99792458 × 10 8 m / s . Many astronomers, this is written before the Planck mission data
has been vetted, believe that the age of the universe is tuniverse = 13.7 ×10 years .
a) The ratio of the Sun’s radius to that of the Earth is given by
9
R 6.96 ×10 8 m
=
= 109 .
R⊕ 6.371 ×10 6 m
.
Using a meter stick to represent the diameter of the Sun, the the diameter of the Earth
would be represented, approximately, by
b)
1 m
−3
≈ 9.2 × 10 m ≡ 9.2 mm .
109
The mean distance from the Sun to the dwarf planet Pluto is, approximately,
rPluto = 5.89 ×1012 m . Express this distance in astronomical units. We have
AU
⎞
12
12 ⎛
rPluto = 5.89 ×10 m ≡ 5.89 × 10 ⎜
11 ⎟ ≡ 39.4 AU .
⎝ 1.496 × 10 ⎠
The nearest star to our own Sun is Proxima Centauri. Its distance is approximately
rProxCent  = 4.05 × 1016 m . Express the distance to Proxima Centauri in
astronomical units. We write
AU
⎞
16
16 ⎛
rProxCent  = 4.05 × 10 m ≡ 4.05 ×10 ⎜
11 ⎟ ≡ 271,000 AU .
⎝ 1.496 ×10 ⎠
c)
While the astronomical unit is useful in the solar system, it is not so useful on
larger scales.
The distance light travels in one year is known as a light-year, and signified by ly .
Express the distance to Proxima Centauri in ly .
(
)(
)
ly ≡ 2.9979 × 108 m / s 3.1536 × 10 7 s ≡ 9.4542 ×1015 m .
Therefore,
ly
⎞
16
16 ⎛
rProxCent  = 4.05 × 10 m ≡ 4.05 ×10 ⎜
15 ⎟ ≡ 4.28 ly .
⎝ 9.4542 ×10 ⎠
d)
Astronomers think that our own galaxy, the Milky Way, is approximately 1.2 × 10 ly
in diameter. Express this diameter in meters. We can write
5
S 1-4
(
)
DMilky Way = 1.2 × 105 ly ≡ 1.2 ×10 5 9.4542 × 1015 m = 1.13 × 1021 m .
e)
If we model the universe as a sphere, then in meters, calculate a reasonable estimate of
the upper limit for the radius of the universe. We have
(
(
)(
Runiverse = ctuniverse = 2.9979 ×10 8 m / s 13.7 × 10 9 years
)(
)(
)
)
= 2.9979 ×10 8 m / s 13.7 ×10 9 3.1536 × 107 s = 1.30 × 10 26 m .
1-6) The SI standard unit for mass in the kilogram, kg . In this exercise, we want you to get some
sense of the range of masses that we find in the universe.
a) One of the smaller objects in the universe is the electron. The measured mass of the
− 31
electron is me = 9.109390 ×10
kg . Calculate the number of electrons one would
need for a total mass equivalent to one kilogram. We have
Ne =
b)
1 kg
30
= 1.098 × 10 .
− 31
9.109390 × 10 kg
The mass of monatomic hydrogen is measured to be mH = 1.673491 × 10
find the ratio of the mass of the hydrogen atom to the mass of the electron.
− 27
kg ,
mH 1.673491 × 10 −27 kg
=
= 1,837 .
m e 9.109390 ×10 − 31 kg
c)
− 27
The mass of a proton is determined to be mp = 1.672623 × 10
the sum of the masses of a proton and an electron.
(
kg . Calculate
)
mp + me = 1.672623 × 10− 27 + 9.109390 × 10− 31 kg = 1.673534 × 10−27 .
d)
How does that sum compare to the mass of a monatomic hydrogen atom?
mp + me = 1.673534 ×10 −27 > mH = 1.673491 × 10− 27 kg .
This suggests that free particles have slightly more mass than bound particles. Also
suggest, if there is to be conservation of energy, that there is something like “binding”
energy. Whatever energy is.
30
The mass of the Sun is measured to be M  = 1.99 × 10 kg . Calculate the ratio of
the mass of the Sun to that of a monatomic hydrogen atom.
M
1.99 ×10 30 kg
57
=
= 1.19 × 10 .
−27
mH 1.673491 × 10 kg
e)
The Sun is made up mostly of hydrogen and helium. Assume the mass is made up
only of hydrogen. Calculate a reasonable estimate of the number of hydrogen
nuclei in the Sun.
N protons = 1.19 ×10 57 .
f)
The mass of the Earth is measured to be M ⊕ = 5.97 × 10
the mass of the Sun to that of the Earth.
M  1.99 × 10 30 kg
5
=
= 3.33 × 10
24
M ⊕ 5.97 ×10 kg
S 1-5
24
kg . Calculate the ratio
g)
It is estimated that there are, on average, N stars per galaxy = 1 × 10 stars per galaxy in
the universe. Assume these stars are, on average, as massive as our own Sun.
Estimate of the mass of an average galaxy.
11
(
)(
)
M ave galaxy = N stars per galaxy M  = 1 ×1011 1.99 × 10 30 kg = 1.99 ×10 41 kg .
11
h) Astronomers estimate that there may be as many as N galaxies = 1 ×10 galaxies in the
universe. If this is accurate, calculate a reasonable estimate for the mass of the
universe.
(
)(
)
M univers = N galaxies M ave galaxy = 1 × 1011 1.99 × 10 41 kg = 1.99 × 1052 kg .
If this mass were made up of hydrogen atoms only, calculate the number of atoms this
would represent.
M universe
1.99 ×10 52 kg
79
NH = N p = Ne =
=
= 1.19 × 10 .
−27
mH
1.673491 × 10 kg
Using the number you found for the radius of the universe, calculate the average mass
density of our model hydrogen universe.
ρuniverse
M universe
1.99 ×10 52 kg
=
=
3
( 4 / 3) π Runiverse
( 4 / 3)π 1.3 ×10 26 m
(
)
3
= 2 ×10 −27
kg
.
m3
All of our exploration of the universe has been predicated on all of the matter being
ordinary, what we call baryonic. We have not stuck our toes, even a tad, into the
realm of dark matter and dark energy!
Calculate your mass. A weight of 2.205 lbs has a mass equivalent to 1 kg .
i)
m ( kg) = W ( lbs ) / 2.205 .
Assume all of your mass is made up of water, H 2 O . Calculate a reasonable estimate of
the number of water molecules in your body.
N H 2O = nN A ,
where n is the number of moles. An atom of oxygen has a molecular mass
M H 2O = 18.015 grams per mole, and Avogadro’s number is N A = 6.02 ×10 23
objects per mole.) The number of moles would be
n=
m ( kg)
W (lbs )
=
= ( 25.17 )W moles .
M H2 O (kg ) 2.205 (lbs / kg) (0.018015 kg/mole )
Therefore,
(
) (
)
N H 2O = nN A = (( 25.17 )W mole ) 6.02 ×10 23 / mole = 1.515 × 1025 W .
1-7) The SI standard unit of time is one second, s . In this exercise, we want you to get some
sense of the range of time values that we find in the universe.
a) The time needed for light to travel a distance of one meter is
t=
b)
1 m
= 3.3356410 ns .
2.99792458 ×10 8 m / s
The time needed for light to travel from the Sun to the Earth is
S 1-6
1.496 ×1011 m
t=
= 499 s ≡ 8.32 min
2.99792458 ×10 8 m / s
c)
A particular atom is approximately 2.0 ×10
cross this atom is
−10
m in diameter. The time for light to
2.0 ×10 −10 m
−19
t=
= 6.7 × 10 s .
8
2.99792458 ×10 m / s
d)
In laboratory experiments with light, scientists have found that light exhibits the peculiar
feature of interacting sometimes like a wave and sometimes like a particle. The particle
of light is called a photon. Photons are produced, among other places, in the cores of
stars as the result of nuclear reactions. Theorists estimate that a photon produced in the
core of the Sun might take as long as 500,000 years to make its way to the surface of
the Sun. Express this time in seconds.
(
)
500,000 years ≡ 500,000 3.1536 × 10 7 s = 1.58 ×1013 s .
A reasonable estimate of the average speed of the photon in this process is
save
R
6.96 × 10 8 m
=
=
= 4.4 × 10−5 m / s ≡ 4.4 µm / s .
13
500,000 yrs 1.58 × 10 s
c
2.9979 × 108 m / s
12
=
= 6.8 × 10 .
-5
save
4.4 ×10 m / s
The speed of light is dependent on the medium through which it passes. Stellar
interiors are quite opaque.
e)
Astrophysicists speculate that stars can not get much more massive than about
120M  . Such super-massive stars have radii of about 100R , where, recall,
R = 6.96 ×10 8 m . The time needed for a signal to travel with speed c from one
edge of such a super-massivve star to the other edge along a diameter is
t=
f)
2 (100R )
c
=
(
) = 464 s ≡ 7.74 min .
m / s)
200 6.96 × 108 m
(2.9979 ×10
8
If the average life expectancy of a human being is 80.0 years , calculate the ratio of this
time to that of the estimated age of the universe. We write
80.0 yrs
−9
= 5.84 ×10
9
13.7 ×10 years
S 1-7
Solutions to Problems for Chapter Two
2-1) Two vectors are given by:


A = 5 î − 4 ĵ + 8 k̂ , and B = −3 î + 7 ĵ − 6 k̂ .
Calculate the following quantities of interest:
a)
b)

 
A = A • A = Ax2 + Ay2 + Az2 = 52 + 4 2 + 8 2 = 105 = 10.2 .
(1)

A
5
4
8
 =  =
î −
ĵ +
k̂ = 0.4880 î − 0.3904 ĵ + 0.7807 k̂
A
105
105
105
= cosθ x î + cosθ y ĵ + cosθ z k̂ .
c)
d)
e)

 
B = B • B = Bx2 + By2 + Bz2 = 32 + 7 2 + 6 2 = 94 = 9.7 .
(3)

B
3
7
6
B̂ =  = −
î +
ĵ −
k̂ =− 0.3094 î + 0.7220 ĵ − 0.6189 k̂ .(4)
B
94
94
94
  
C = A + B = ⎡⎣ 5 î − 4 ˆj + 8 k̂ ⎤⎦ + ⎡⎣−3 î + 7 ĵ − 6 k̂ ⎤⎦
= 2 î + 3 ĵ + 2 k̂ .



C = 3B − 2 A = 3 ⎡⎣−3 î + 7 ˆj − 6 k̂ ⎤⎦ − 2 ⎡⎣ 5 î − 4 ĵ + 8 k̂ ⎤⎦
f)
g)
h)
i):
(2)
= −19 î + 29 ĵ − 34 k̂ .
  
C = A × B = î ⎡⎣ Ay B z − Az By ⎤⎦ + ĵ ⎡⎣ A z Bx − Ax B z ⎤⎦ + k̂ ⎡⎣ Ax B y − A y Bx ⎤⎦
= î ⎡⎣ (−4 )(−6 ) − ( 8) (7 )⎤⎦ + ĵ ⎡⎣( 8 )(−3) − ( 5) (−6 )⎤⎦ + k̂ ⎡⎣ (5 )( 7 ) − (−4 ) (−3)⎤⎦
(5)
(6)
= î [24 − 56 ] + ĵ [−24 + 30 ] + k̂ [ 35 − 12] = −32 î − 6 ĵ + 23 k̂ .
(7)
 
C = A • B = ⎡⎣ 5 î − 4 ĵ + 8 k̂ ⎤⎦ • ⎡⎣−3 î + 7 ĵ − 6 k̂ ⎤⎦ = −15 − 28 − 48 = −91 . (8)

e)
For
C = 2 î + 3 ĵ + 2 k̂ ,
(9)

2
2
2
the magnitude is C = 2 + 3 + 2 = 17 = 4.1 ,
(10)
while
 a unit vector is given by
 C
2
3
2
C=  =
î +
ĵ +
k̂ = 0.4851 î + 0.7276 ĵ + 0.4851 k̂
C
17
17
17
= cosθ x î + cosθ y ĵ + cosθ z k̂ .
Therefore,
while
θ x = θ z = cos−1 ⎡⎣ 2 / 17 ⎤⎦ = 61.0° ,
θ y = cos−1 ⎡⎣ 3 / 17 ⎤⎦ = 43.3° .
S 2-1
(11)
(12)
(13)
f)

C = −19 î + 29 ĵ − 34 k̂ ,
For
(14)

C = 192 + 292 + 34 2 = 2,358 = 48.6 ,

C
19
29
34
Ĉ =  = −
î +
ˆj −
k̂
C
2,358
2, 358
2, 358
while
(15)
= −0.3913 î + 0.5972 ĵ − 0.7002 k̂ = cos θ x î + cosθ y ĵ + cos θ z k̂ .
Therefore,
θ x = 113.0° ; θy = 53.3° ; θz = 134.4° .

g)
For
C = −32 î − 6 ĵ + 23 k̂ ,

C = − 32 2 + 6 2 + 232 = 1,589 = 39.9 ,

C
32
6
23
while
Ĉ =  = −
î −
ĵ +
k̂
C
1,589
1, 589
1,589
(16)
(17)
(18)
(19)
= −0.8028 î − 0.1505 ĵ + 0.5770 k̂ = cos θ x î + cos θ y ĵ + cos θ z k̂ . (20)
Therefore,
θ x = 143.4° ; θy = 98.7° ; θz = 54.8° .
(21)
2-2) A vector is given by

F = 24 î −13 ĵ − 35 k̂ .
Calculate the values of the angles θ x , θ y and θ z .
The magnitude of this vector is

F = 24 2 +132 + 352 = 1,970 = 44.38 .
We use the dot product to find the angles. We have
(1)

F • î = Fx = F cosθ x → θ x = cos −1 ( Fx / F ) = cos−1 24 / 1, 970 = 57.3° , (2)
and

F • ĵ = Fy = F cosθ y → θy = cos−1 Fy / F = cos −1
(
)
while
(
( −13 /
)
)
1,970 = 107° , (3)

F • k̂ = Fz = F cosθ z → θz = cos−1 (Fz / F ) = cos−1 −35 / 1,970 = 142.1° . (4)


2-3) Two vectors A and B have equal magnitudes of 2 . Solve graphically for the following:
a)
the angle between them if the magnitude of their sum is 3 .
b)
the angle between them if the magnitude of their sum is 2 .
c)
the angle between them if the magnitude of their
 sum is 4.
The diagram below suggests that if we add vector B to vector A , the sum must be
(
)
somewhere on the circumference of the circle. Using the dot product to play with magnitudes, we
have
 
C2 = A + B
(








) • ( A + B) = A • A + 2 A • B + B • B = A
2
+ B 2 + 2AB cosθ
= A 2 + B 2 + 2ABcos θ = 8 + 8 cos θ = 8 (1 + cosθ ) .
S 2-2
(1)
(
)
C 2 / 8 = 1 + cosθ → θ = cos −1 ⎡⎣ C 2 / 8 − 1⎤⎦ .
Also,

 =C
 +B
A
For C = 3 ,
b)
For C = 2 ,

B
θ

A
a)
(2)
θ = cos−1 ⎡⎣( 32 / 8 ) −1⎤⎦ = 82.8° .
θ = cos−1 ⎡⎣( 22 / 8) − 1⎤⎦ = 120° . θ = cos−1 ⎡⎣( 4 2 / 8 ) − 1⎤⎦ = 0° .
2-4) A straight line of magnitude 6 km is directed 30° west of north. Calculate:
c)
For C = 4 ,
a)
b)
the magnitude of the westerly component of the line,
the magnitude of the northerly component. (A diagram might prove useful.)
(3)
(4)
(5)
()
North ĵ
6 km
ϕ
()
East î
a)
b)
The magnitude of the westerly component is given by
(6 km )( sin 30°) = 3 km .
(1)
The magnitude of the northerly component is given by
(6 km )( cos 30°) = 5.2 km .
2-5) Given:
find the unit vector in the direction of

A = 2 î + ˆj − k̂ ,

B = −3 î + 2 ĵ + k̂ ,
S 2-3
(2)



C = 2B − 3A .

Vector C is given by

C = 2 ⎡⎣−3 î + 2 ĵ + k̂ ⎤⎦ − 3 ⎡⎣ 2 î + ĵ − k̂ ⎤⎦
= −12 î + ĵ + 5 k̂ .

The magnitude of vector C is given by

C = C = 12 2 + 12 + 52 = 170 = 13.04 .
(1)
(2)
Therefore, a unit vector can be found by
C
12
1
5
Ĉ =  =−
î +
ĵ +
k̂ =−0.9204 î + 0.0767 ˆj + 0.3835 k̂
C
170
170
170
= cosθ x î + cosθ y ĵ + cosθ z k̂ .
(3)
2-6) Show that if the sum of three vectors is zero, they must all lie in the same plane.
In a Cartesian coordinate system wecan write
 
A + B +C = 0.
(1)
This requires
Ax + Bx = −C x , Ay + By = −C y , Az + Bz = −C z .
(2)
Therefore,
 

A+ B=−C.
(3)
Vectors that are opposite must lie in the
same
plane.



2-7) In the diagram below, vectors A and B are position vectors. Vector
C
is the position

vector for the midpoint of the line segment that joins the tips of vectors A and B . Prove:
 1  
C=
A+ B .
2
(
()
)
y ĵ

A

C

B
()
x î

We define vector D by
S 2-4
  
D = B − A.
  1 
C = A+ D ,
2
  1 
C = B− D.
2
Therefore,
while
(1)
(2)
(3)
Adding equations (2) and (3) leads to our desired result. We have
  
 1  
2 C = A + B → C = A + B .
(4)
2


2-8) Vector A has a magnitude of 5 and is directed 37° north of east. Find a vector B such that
their sum is directed west with a magnitude of 3 . (East is î and north ĵ .)
(
)
()
North ĵ

B
5

A
()
3
37°
East î
  
C = A+ B
We require
5 cos 37° + Bx = −3 ,
and
5 sin 37° + B y = 0 .
Equation (1) implies
Bx = −3 − 5 cos37° = −7 ,
while equation (2) gives us
By = −5 sin 37° = −3 .

Therefore,
B =−7 î − 3 ĵ .


2-9) Find the angle between the vectors F1 = 2 î − 4 ˆj and F2 = 4 î + 6 ĵ .
(1)
(2)
(3)
(4)
(5)
We note first that the magnitudes are given by


F1 = 2 2 + 42 = 20 = 2 5 , and F2 = 4 2 + 6 2 = 52 = 2 13 .
The dot product gives us
 
 
F1 • F2 = F1 F2 cos ∠bet = 2 î − 4 ĵ
Therefore,
(
) (4 î + 6 ĵ ) = 8 − 24 = −16 .
•
⎡
⎤
−16
⎢
⎥ = 120° . ∠bet = cos
⎢ 2 5 2 13 ⎥
⎣
⎦
2-10) Two vectors are given by


A = 3 î − 2 ĵ , and B = − î + 5 ˆj .
−1
(
)(
S 2-5
)
(1)
(2)
(3)






Find a vector C in the x - y plane such that C = A + B and Ĉ is perpendicular to A + B .
First, we note that
  
D = A + B = 3 î − 2 ĵ + − î + 5 ĵ = 2 î + 3 ĵ .
The magnitude is given by
We require:
(
) (
)
(1)


 
C = D = A + B = 2 2 + 32 = 13 .
 
C • D = 0 = C x ( 2 ) + C y ( 3) ,
(2)
C x2 + Cy2 = 13 .
(4)
and
(3)
Equation (3) implies
C x = −C y ( 3 / 2) .
Substitution of equation (5) into equation (4) yields
( − ( 3 / 2) C )
2
y
and
(5)
+ C 2y = 13 = (13 / 4 ) C 2y ,
(6)
C y = ±2 .
(7)
C x = − ( ±2) (3 / 2 ) = 3 ,


D =− 3 î + 2 ˆj or D = 3 î − 2 ĵ .
Therefore,
and
2-11)
(8)
(9)

A


B

Two vectors A and B are adjacent sides of a parallelogram, as represented in the diagram above.
Do the following


a)
Derive expressions for the two diagonals in terms of A and B .
b)
a)


Prove the diagonals will be perpendicular if A = B .


c)
Prove that A × B is the area of the parallelogram.
We can write

 
D1 = A − B
which implies
 
 
D1 • D1 = D12 = A − B
(



(1)





) • ( A − B) = A • A − 2 A • B + B • B
= A 2 + B 2 − 2ABcos θ ,
S 2-6
(2)

D1

A
ϕ
r⊥
θ
θ
r⊥

D2

B
For the second diagonal, we can write 
 
D2 = A + B ,
 
 
 
 
   
D2 • D2 = D22 = A + B • A + B = A • A + 2 A • B + B • B
(
and
b)
)(
)
= A 2 + B 2 + 2BAcos θ .
If we take the dot product of the two diagonals, we find
 
 
 
   
D1 • D2 = A − B • A + B = A 2 + A • B − B • A − B 2 = A 2 − B 2 .
(
) (
)
(3)
(4)
(5)
Now, if the diagonals are perpendicular,
 then
 we require
D1 • D2 = 0 = A 2 − B 2 ,
A = B.
(6)
which requires:
(7)
c) Inspection of the diagram above should convince one that r⊥ , the so-called altitude, is given
r⊥ = A sin θ .
(8)
⎛1
⎞
A = ( r⊥ )( B − A cos θ ) + 2 ⎜ ( A cosθ )( r⊥ )⎟ ,
⎝2
⎠
(9)
by:
Also, the area of the parallelogram is
where the first term is the area of the rectangle and the second term is the area of the two triangles
that make up the total area of the parallelogram. So, we have
A = r⊥ B − r⊥ A cosθ + r⊥ A cosθ = r⊥ B = AB sin θ .
(10)
Now, by definition,
 
A × B = AB sin ∠bet = AB sin θ = A .
(11)
2-12) A point mass m is moving with constant
 speed v along a circular path of radius R , as
indicated below. The instantaneous velocity v is directed along a line tangent to the circle; a
ˆ . Using the information above, do the following:
direction signified by the unit vector ϕ
a)
Write an expression for the position vector in terms of the unit vector rˆ .
b)
Write an expression for the position vector in terms of the unit vectors î and ĵ .
ˆ.
c)
Write an expression for the velocity vector in terms of the unit vector ϕ
d)
Write an expression for the velocity in terms of the unit vectors î and ĵ .
ˆ and rˆ are perpendicular to each other.)
(The unit vectors ϕ
S 2-7
()
y ĵ

v ϕ̂
r̂ m

r
ϕ
()
x î
R
a)
We have
b)
We can write
Equations (1) and (2) imply

r = R r̂ .
(
(1)
)

r = R cos ϕ î + sin ϕ ĵ .
(2)
r̂ = cos ϕ î + sin ϕ ĵ .
(3)
c) By definition,

dR
dr̂
 dr d
v=
= [ R r̂ ] =
r̂ + R
.
(4)
dt dt
dt
dt
The radius is constant, so (dR / dt ) = 0 and equation (4) becomes
d
dϕ
dϕ ˆ ⎤

⎡
v = R ⎡⎣ cos ϕ î + sin ϕ ˆj ⎤⎦ = R ⎢ − sin ϕ
î + cos ϕ
j
dt
dt
dt ⎥⎦
⎣
dϕ
⎡ − sin ϕ î + cosϕ ĵ ⎤ = Rω ϕ̂ ,
=R
(5)
⎦
dt ⎣
where we have introduced the so-called angular speed ω , defined by
dϕ
ω=
,
(6)
dt
and the unit vector ϕ̂ defined by
ϕ̂ = − sin ϕ î + cos ϕ ĵ .
(7)
The unit vector r̂ signifies the so-called radial direction (centrifugal) direction. The unit vector ϕ̂
is perpendicular to r̂ and signifies the so-called tangential direction. To recapitulate,

v = v ϕ̂ = Rω ϕ̂ .
(8)
S 2-8
d)
In Cartesian coordinates, the velocity is given by

v = v ⎡⎣ − sin ϕ î + cos ϕ j ⎤⎦ = Rω ⎡⎣ − sin ϕ î + cos ϕ j ⎤⎦ .
(9)
2-13) Experiment confirms that if a point mass m is subjected, simultaneously, to N forces, then
its physical
response is the same as if it had been subjected to a single force, the net force, signified

by Fnet and defined by
N 

 


Fnet = F1 + F2 + + Fi + FN = ∑ Fi .
i=1
This result is called the superposition principle.
Suppose that an object is acted on by the following three forces simultaneously:

F1 = F1 F̂1 = 12 N î + 8 N ĵ − 6 N k̂ ,

F2 = F2 F̂2 = −8 N î + 10 N ĵ − 2 N k̂ ,

F3 = F3 F̂3 = 6 N î − 6 N ĵ + 6 N k̂ .
a)
b)
c)

a)
Draw a careful diagram of these forces, and include the net force Fnet .
b)
Find the magnitude of the net force.
c)
Find a unit vector representing the direction of the net force.
The net force is given by

 

Fnet = F1 + F2 + F3 = ⎡⎣10 î + 12 ĵ − 2 k̂ ⎤⎦ N .
(1)
The magnitude of the net force is given by

Fnet = 102 +12 2 + 2 2 N = 248 N = 15.75 N .
(2)
A unit
 vector can be found using
F
10
12
2
F̂net = net =
î +
ĵ −
k̂ = 0.6350 î + 0.7620 ˆj − 0.1270 k̂
Fnet
248
248
248
= cosθ x î + cosθ y ĵ + cosθ z k̂ .
2-14)
(3)
()
z k̂

r

r1

r2
()
y ĵ
()
x î
Two position vectors are given by
S 2-9

r1 = x1 î + y1 ĵ + z1 k̂ ,

r2 = x2 î + y2 ĵ + z2 k̂ ,
as represented in the diagram above. Do the following



a)
Write an expression for vector r in terms of vectors r1 and r2 .

b)
Use the dot product to find an expression for the magnitude
of
vector
r.

c)
Calculate a unit vector to represent the direction of vector r .
a) The position vector is given by
   ⎡
r = r2 − r1 = ⎣ x 2 î + y2 ĵ + z 2 k̂ ⎤⎦ − ⎡⎣ x1 î + y1 ĵ + z1 k̂ ⎤⎦
= ( x2 − x1 ) î + ( y 2 − y1 ) ĵ + ( z2 − z1 ) k̂ .
b)
(1)
The magnitude of the position vector is given by

r =
•
r r
= ⎡⎣( x 2 − x1 ) î + ( y2 − y1 ) ĵ + (z 2 − z1 ) k̂ ⎤⎦ • ⎡⎣ ( x2 − x1 ) î + ( y2 − y1 ) ĵ + ( z2 − z1 ) k̂ ⎤⎦
( x 2 − x1 )2 + ( y2 − y1 )2 + ( z2 − z1 )2
=
.
(2)
(You may recognize this as the so-called distance formula.)
c) A unit vector for this vector can be found using
=
Note:
2-15)
( x2 − x1 )

r

r ( x2 − x1 ) î + ( y2 − y1 ) ĵ + ( z2 − z1 ) k̂
r̂ =  =
r
( x2 − x1 )2 + ( y2 − y1 )2 + ( z2 − z1 )2
î +
( y2 − y1 )

r
ĵ +
(z2 − z1 )

r
k̂ == cos θ x î + cosθ y ĵ + cos θ z k̂ . (3)
⎡x −x ⎤
⎡y −y ⎤
⎡z − z ⎤
θ x = cos −1 ⎢ 2  1 ⎥ ; θ y = cos−1 ⎢ 2  1 ⎥ ; θz = cos−1 ⎢ 2  1 ⎥ . (4)
⎣ r ⎦
⎣ r ⎦
⎣ r ⎦
y
y′
x
x′
y′

r
x′
y
θ
ϕ
θ
x
S 2-10
A two-dimensional Cartesian coordinate system with axes x ′ and y ′ is rotated an angle θ
from a second Cartesian coordinate system with axes x and y , as represented in the diagram
above. Do the following:

a)
Find the components of the position vector r in each system.
b)
Use the results of part a) to calculate the how the components of the primed system are
related to those of the unprimed system. The trigonometric identity for cos (ϕ − θ )
may prove useful. (The magnitude of a vector is invariant under a rotation.
Mathematicians use this to define what a vector is: any quantity the components of
which transform in the way represented here.)
a) We can write

r = x î + y ˆj = x ′ ˆi ′ + y′ ˆj ′ .
y
(1)
y′
x
θ
in θ
θ

r
x′
xs
y
y′
x′
y
ϕ
θ
θ
cos
nθ
y si
θ
x
x ′ = x cosθ + y sin θ ,
y ′ = −x sin θ + y cosθ
b) We can write:
and
2-16)
(2)
z


B



A
x
S 2-11
y
Three edges of a cube of side length  lie along the x , y and z axes, respectively, is
represented in the diagram above. Do the following:

a)
Find the angle between vector B
 , a body diagonal, and the z-axis.

b)
Find the angle between vector A , a face diagonal, and vector B .
a) The vectors are given by:


A =  î +  ĵ ; B =  î +  ĵ +  k̂ ,


which implies:
A= 2 ; B = 3 .

To find θ , the angle vector B makes to the z -axis, we use the dot product. We find


k̂ • B = k̂ B cos θ = Bz =  3 cosθ =  .
(1)
(2)
(3)
Therefore,
⎡  ⎤
θ = cos−1 ⎢
= cos −1 ⎡⎣ 3−1/ 2 ⎤⎦ = 54.74° .
⎥
⎣ 3⎦
(4)
z

B

θ

ϕ

A

x

y

b) To find ϕ , the angle between vector A and B , we take the dot product of the two vectors
and get
 
 
A • B = A B cos ϕ = A x Bx + Ay B y + Az Bz
( )( )
=  2  3 cos ϕ = ( ) ( ) + ( )(  ) + (0 )(  ) = 22 .
Therefore,
⎡ 2 ⎤
ϕ = cos −1 ⎢
= cos−1 ⎡⎣ 2 ⋅ 6−1/ 2 ⎤⎦ = 35.26° .
⎥
⎣ 6⎦
Note that angles θ and ϕ are complimentary, as we would expect.
2-17) Show that

 
  
  
A × B × C = B A • C − C A• B .
(
)
(
)
(
(5)
(6)
)
We assume the vectors are in a Cartesian coordinate system. First, we break the equation up into
S 2-12
more manageable parts. From what we know about the cross product, we can write
 
B × C = î ⎡⎣ B yC z − Bz C y ⎤⎦ + ĵ ⎡⎣ Bz C x − Bx Cz ⎤⎦ + k̂ ⎡⎣ Bx Cy − ByC x ⎤⎦ .

 
A× B×C
So,
(
(
(
)
)
)
(1)
= î ⎡⎣ Ay BxC y − ByC x − Az ( Bz C x − Bx C z )⎤⎦
+ ĵ ⎡⎣ Az B yC z − Bz C y − Ax Bx C y − B yC x ⎤⎦
+ k̂ ⎡⎣ Ax ( Bz C x
(
− B C ) − A (B C
x
z
y
y
z
)
− B C )⎤⎦
z
y
= î ⎡⎣ Ay B xC y − A y By Cx − Az Bz C x + Az Bx Cz ⎤⎦
+ ĵ ⎡⎣ Az ByC z − Az B z Cy − Ax BxC y + Ax B yC x ⎤⎦
+ k̂ ⎡⎣ Ax Bz C x − A x B xC z − Ay B yC z + Ay B z Cy ⎤⎦ .
Next, we note
  
B A • C = ⎡⎣ Bx î + B y ˆj + Bz k̂ ⎤⎦ Ax C x + A yC y + A zC z
= î ⎡⎣ Ax B xC x + Ay B xC y + A z BxC z ⎤⎦
(
(
)
(2)
)
+ ĵ ⎡⎣ Ax B yC x + Ay By C y + Az B yC z ⎤⎦
Now, we calculate
+ k̂ ⎡⎣ Ax Bz C x + A y Bz C y + A z B z Cz ⎤⎦ .
  
− C A • B = ⎡⎣ −C x î − C y ˆj − Cz k̂ ⎤⎦ Ax B x + A y By + Az Bz
= − î ⎡⎣ Ax Bx C x + A y ByC x + Az Bz C x ⎤⎦
(
(
)
(3)
)
− ĵ ⎡⎣ Ax B xC y + Ay By C y + Az Bz C y ⎤⎦
− k̂ ⎡⎣ Ax Bx Cz + A y By Cz + A z B z Cz ⎤⎦ .
(4)
Adding the x -components of equations (3) and (4) yields
î ⎡⎣ A x B xC x + A y Bx C y + Az B xC z − Ax Bx Cx − Ay ByC x − Az Bz C x ⎤⎦
= î ⎡⎣ Ay B xC y + A z B xC z − A y ByC x − Az Bz C x ⎤⎦ .
(5)
Comparing the x -component of equation (2) with equation (5) we see that they are equal!
Adding the y -components of equations (3) and (4) we find
ĵ ⎡⎣ A x By C x + A y ByC y + Az ByC z − A x Bx C y − A y ByC y − Az Bz C y ⎤⎦
= ĵ ⎡⎣ Ax B yC x + A z ByC z − Ax Bx Cy − Az Bz C y ⎤⎦ .
Equation (6) is also identical to the y -component of equation (2)!
Adding the z -components of equations (3) and (4) gives us
S 2-13
(6)
k̂ ⎡⎣ Ax B z Cx + Ay Bz C y + Az Bz C z − A x Bx Cz − Ay By Cz − Az Bz C z ⎤⎦
= k̂ ⎡⎣ Ax Bz C x + A y Bz C y − A x Bx C z − Ay B yC z ⎤⎦ .
(7)
Finally, we compare equation (7) with the z -component of equation (2) and see they are equal!
Therefore,

 
  
  
A × B × C = B A • C − C A • B . QED
(8)
 

2-18) A parallelopiped, the adjacent edges of which are vectors A , B and C , is represented in the
diagram below. Show that the volume V of the parallelopiped is given by
  
V = A• B × C .
(
)
(
)
(
(
)
)
The volume of a parallelopiped is given by the product of the area of the base, the
parallelogram, times the altitude, V parallelopiped = r⊥2 Abase . As we say earlier, the area of a
parallelogram is given by



A = r⊥1 B = C sin θ B = BC sin θ .
(
So, the volume would be
)
(1)
V parallelopiped = r⊥2 ( BC sinθ ) = ( A sin ϕ ) ( BC sin θ ) = ABC sin θ sin ϕ .
(2)

ĵ C
base
r⊥1
θ

A

B
r⊥2
î

C
ϕ θ
k̂
r⊥1
ĵ

B

î

First, we note vectors B and C define a plane; we will assume it is the x - y plane.

Vector A can be written as
 
 
B × C = B C sin θ k̂ = BC sin θ k̂ .
()
S 2-14
(3)

A = A x î + Ay ĵ + A sin ϕ k̂ .
Therefore,
  
A • B × C = ⎡⎣ Ax î + A y ĵ + A sin ϕ k̂ ⎤⎦ • ⎡⎣ BC sin θ k̂ ⎤⎦
= ABC sin θ sin ϕ = V parallelopiped .
(
(4)
)
S 2-15
(5)
Solutions to Problems for Chapter Three
3-1) At time t = 0 , a child on a merry-go-round starts at a point on the +y -axis and walks
toward the +x -axis on a circular path of circumferential length  = 8 m with a constant speed,
relative to the merry-go-round, of v = 1 m / s Do the following:
a)
Calculate the child’s displacement, relative to the merry-go-round over the time
interval Δt = 1 s .
b)
Calculate the average velocity of the child over the time interval Δt = 3 s .
c)
Calculate the average acceleration from time t = 1 s to t = 3 s .
a)
y
to
Δ = Rθ

Δr

ro
t

r
θ
x
In general,
(
)
  
Δr = r − ro = R sin θ î + cos θ ˆj − R = R ⎡⎣ sin θ î − (1 − cos θ ) ĵ ⎤⎦ ,
Rθ = vt → θ = vt / R .
while
From the information given, we can write
(1)
(2)
2π R = C = 8 → R = 4 / π .
(3)
θ = vt / (4 / π ) = π vt / 4 .
(4)
The results of equation (3) into equation (2) yields
Using equations (3) and (4) in equation one gives us
⎛
 4 ⎡ ⎛ π vt ⎞
⎛ π vt ⎞ ⎞ ⎤
Δr = ⎢ sin ⎜
î − ⎜ 1 − cos ⎜
ĵ .
⎟
⎝ 4 ⎟⎠ ⎟⎠ ⎥⎦
π⎣ ⎝ 4 ⎠
⎝
So, for t = 1 . equation (5) gives us
b)
⎛
⎛ π (1)(1) ⎞ ⎞
 4 ⎡ ⎛ π (1)(1) ⎞
Δr = ⎢ sin ⎜
î
−
1−
cos
⎜⎝ 4 ⎟⎠ ⎟⎠
⎜⎝
π ⎢⎣ ⎝ 4 ⎟⎠
The average velocity is defined by
S 3-1
(5)
⎤
ĵ ⎥ = 0.90 m î − 0.37 m ĵ . (6)
⎥⎦

Δr
4 ⎡ ⎛ π vt ⎞
⎛

⎛ π vt ⎞ ⎞ ⎤
vave =
=
⎢ sin ⎜⎝
⎟⎠ î − ⎜ 1 − cos ⎜⎝
⎟ ĵ ⎥ .
Δt π Δt ⎣
4
⎝
4 ⎠ ⎟⎠ ⎦
For t = Δt = 3 s , we have

⎛
Δr
4 ⎡ ⎛ π (1) (3) ⎞
⎛ π (1)( 3) ⎞ ⎞

vave =
=
î
−
1
−
cos
⎢ sin ⎜
⎜⎝ 4 ⎟⎠ ⎟⎠
⎜⎝
Δt π ( 3) ⎢⎣ ⎝ 4 ⎟⎠
(
)
(7)
⎤m
ĵ ⎥
⎥⎦ s
= 0.30 î − 0.72 ĵ m / s .
c)
The average acceleration is defined by
(8)

Δv

aave =
,
Δt

(9)
where v is an instantaneous velocity.
ĵ
t1

r1

v1
î

r3
t3

v1

So, Δv is given by
(
  
Δv = v3 − v1 = v [v̂ 3 − v̂1 ]
) (
)
(
)
= v ⎡⎣ − cos45° î − sin 45° ĵ − cos 45° î − sin 45° ĵ ⎤⎦ = v −2 cos 45° î , (10)
Therefore,
(
)

2 (1 m / s ) 2 / 2
Δv
2v cos 45°

2
aave =
=−
î = −
î =− 0.707 m / s î . (11)
Δt
Δt
( 2 s )
3-2) At time t = 0 , a particle is at the origin of a Cartesian coordinates system moving with a
speed of 15 m / s directed at an angle 37° above the horizontal x -axis. At time t = 5 s , the

particle’s position is given by r = 20 m î + 35 m ĵ with a speed of 30 m / s directed at an
angle 53° above the horizontal. Do the following:
S 3-1
a)
b)
Calculate the average velocity of the particle over this 5 s interval.
Calculate the average acceleration of the particle over this same interval.
ĵ

v
53°
t = 5s

Δr

vo
37°
to = 0
a)
b)
î
The average velocity is given by

Δr 20 m
35 m
m
m

vave =
=
î +
ĵ = 4 î + 7 ĵ .
Δt
5 s
5 s
s
s
The average acceleration is given by
(
)
(
(1)
)

Δ v ( 30 m / s ) cos 53° î + sin 53° ĵ − (15 m / s ) cos37° î + sin 37° ĵ

aave =
=
Δt
5 s
= 1.2 m / s 2 î + 3.0 m / s 2 ĵ .
(2)
3-3) A rock of mass m = 0.085 kg is thrown with an initial speed of 25 m / s at an angle of
53° above the horizontal from a cliff that is 100 m in height above level ground. Assuming air
resistance is negligible, find the following quantities of interest:
a)
The time of flight.
b)
The maximum height.
c)
The maximum horizontal range.
d)
The velocity of the rock upon impact.
For constant acceleration, the equations of motion are
  
v = vo + at ,
(1)
and
(2)
  

r = ro + vo t + (1 / 2 ) at 2 .
The table below, helps us generate the specific equations of motion for this set of initial
conditions and constraints.

ro

vo

a
x
y
0
ho
vo cosθ o
vo sin θo
0
−g
So, the velocity components are given by
S 3-2
v x = vo cos θo ,
v y = v o sin θ o − gt .
and
(3)
(4)
The coordinates of the position vector are
x = vo (cos θ o ) t ,
(5)
y = ho + vo ( sin θ o ) t − (1 / 2 ) gt 2 .
and
ĵ

vo
to = 0
(6)
ttop vo cosθ o
θo
m
hmax
ho
tf
θ f î

vf
xR
a)
To find the time of flight, we note that y = 0 when t = t f . So, equation (6) becomes
0 = ho + vo (sin θ o ) t f − (1 / 2) gt 2f .
(7)
To solve this quadratic equation for t f , we multiply equation (7) by −2 / g ; the objective being to
get the coefficient on the quadratic term to be one. We have
⎡ v sinθo ⎤
2ho
t 2f − 2 ⎢ o
t
−
=0.
f
⎥
g
⎣ g ⎦
(8)
The roots of this quadratic equation are
2
⎡ v sinθo ⎤
⎡ v sin θ o ⎤
2h
tf = ⎢ o
± ⎢ o
+ o ,
⎥
⎥
g
⎣ g ⎦
⎣ g ⎦
(9)
where the negative is not physically relevant. Therefore, the time of flight is
⎡ 25 ( sin 53°) ⎤
⎡ 25 ( sin 53°) ⎤
2 (100 )
tf = ⎢
s+ ⎢
+
s = 7 s .
(10)
⎥
⎥
9.81
9.81
9.81
⎣
⎦
⎣
⎦
b)
To find the maximum height, we note y = hmax and vy = 0 when t = ttop . Using equation
(4) yields
0 = vo sinθo − gttop ,
(11)
⎡ 25 sin 53° ⎤
ttop = ⎢
and
(12)
⎥ s = 2.035 s .
⎣ 9.81 ⎦
2
Using this time in equation (6) will get our desired result. We find
S 3-3
2
hmax = ho + vo ( sin θ o ) ttop − (1 / 2 ) gttop
c)
2
= ⎡⎣100 + (25 sin 53°) (2.035 ) − (1 / 2 ) (9.81) (2.035 ) ⎤⎦ m = 120 m . (13)
We note x = x R when t = t f . Therefore, the maximum horizontal range is given by
xR = vo (cosθ o )t f = ( 25 cos53°) ( 7) m = 105 m .
d)
(14)
The y -component of the final velocity is given by
v fy = vo sin θ o − gt f = ⎡⎣ 25 sin 53° − (9.81 )( 7) ⎤⎦ m / s = −48.7 m / s , (15)
while the x -component is
v fx = vo cos θ o = 25 cos53° m / s = 15 m / s .
(16)
Therefore,

v f = 15 m / s î − 48.7 m / s ĵ .
(17)
3-4) A baseball of mass m = 145 grams is thrown horizontally with a speed 30 m / s to a
catcher 18.3 m away. Assuming the air resistance is negligible and we can ignore spin effects, do
the following:
a)
Calculate the vertical distance the ball will have moved before being caught.
b)
Calculate the angle at which the ball should be thrown so that it would be caught at
the same height from which it was thrown. Assume the same initial speed.
a)
ĵ

vo
î
to = 0
t
For these initial conditions and constraints, we have
So, we have
x y

ro 0 ho

vo vo 0

a 0 −g
  
v = vo + at ,
  

r = ro + vo t + (1 / 2 ) at 2 .
(1)
and
The coordinates of the position vector at the time of interest are
x = vo t ,
(2)
and
(4)
y = − (1 / 2 ) gt 2 .
S 3-4
(3)
solving equation (3) for t and substituting it into equation (4) yields
y = − (1 / 2 ) g ( x / vo ) = − (1 / 2 )( 9.81)(18.3 / 30 ) m = −1.83 m .
2
2
(5)
b)
ĵ
î
θo

vo
to = 0
tf

ro

vo

a
x
y
0
0
vo cosθ o
vo sin θo
0
−g
x = vo (cos θ o ) t ,
So,
y = vo sin θ o t − (1 / 2 ) gt 2 .
The y -coordinate is zero when t = t f , and equation (7) implies
and
0 = vo sinθo t f − (1 / 2) gt 2f ,
gt f
sinθo = (1 / 2 )
.
vo
and
equation (6) implies
and
xR = vo (cosθ o )t f ,
xR
tf =
.
vo cos θo
(6)
(7)
(8)
(9)
(10)
(11)
Equation (11) into equation (9) gives us
and
Therefore,
⎛ xR ⎞
g⎜
⎝ vo cos θ o ⎟⎠
sinθo = (1 / 2 )
,
vo
gx
2 sin θ o cosθ o = 2R = sin 2θ o .
vo
⎡ ( 9.81)(18.3 ) ⎤
⎡ gx ⎤
θ o = (1 / 2 ) sin −1 ⎢ 2R ⎥ = (1 / 2 ) sin −1 ⎢
⎥ = 5.75° .
2
⎢⎣ (30 )
⎥⎦
⎣ vo ⎦
S 3-5
(12)
(13)
(14)
3-5) A rocket of mass m = 2.125 kg is launched from rest at an angle 70° to the horizontal.
2
The propulsion system is able to maintain a constant, net acceleration of 8 m / s along its initial
direction for 6.5 s . After the engine shuts down, the rocket is in free-fall. Calculate the following:
a)
The maximum height.
b)
The maximum horizontal range. Assume it was launched from the ground.
ˆj ′

vo
ĵ
hmax
′
θo
ˆi ′
t = 6.5 s ; t ′o = 0
70°
î
to = 0
For the first 6.5 s , the rocket is subjected to a constant acceleration of
(
)(
)

a = 8 m / s 2 cos 70° î + sin 70° ĵ = 2.736 m / s 2 î +7.518 m / s 2 ˆj .
(1)
So, the velocity of the rocket at the time the engines shut off is given by
 

v = at = 17.8 m / s î + 48.9 m / s ĵ = vo′ ,
(2)
and the distance it has traveled horizontally is given by
Δx = (1 / 2 ) ax t 2 = (1 / 2 ) (2.736 ) (6.5 ) m = 57.8 m ,
2
(3)
while the vertical distance it has traveled is given by
Δy = (1 / 2 ) ayt 2 = (1 / 2 )( 7.518 )( 6.5 ) m = 158.8 m .
2
(4)
Once the engines are off, the rocket is in free-fall, and the initial conditions and constraints in
the primed system, as represented above is given by
x

ro′ 0

vo′ vox′

a′ 0
while
and
as well as
y
0
voy′
−g
v ′y = v ′oy − gt ′ ,
x ′ = vox′ t ′ ,
y ′ = voy
′ t ′ − (1 / 2) gt ′ 2 .
S 3-6
(5)
(6)
(7)
We have seen this before, at maximum height, t ′ = ttop
′ and y ′ = hmax
′ and v ′y = 0 . So,
equation (5) becomes
0 = voy′ − gttop
′ ,
(8)
[
]
and
ttop
′ = voy′ / g = 48.9 / 9.81 s = 5 s .
This result substituted into equation (7) yields
2
hmax
′ = ⎡⎣( 48.9 )(5 ) − (1 / 2 )( 9.81)( 5) ⎤⎦ m = 122 m .
Therefore,
b)
(9)
(10)
hmax = h′max + Δy = 122 m +159 m = 281 m .
For the time of flight, t ′ = t ′f , when y ′ = −Δy . Equation (7) becomes
and
(11)
−Δy = voy′ t ′f − (1 / 2 ) gt ′f 2 ,
(12)
⎛ 2voy′ ⎞
2Δy
t ′f2 − ⎜
t
′
−
=0.
f
⎝ g ⎟⎠
g
(13)
Therefore,
2
2
′ ⎞
⎛ v oy
2Δy ⎡ 48.9
2 (159 ) ⎤
⎛ 48.9 ⎞
⎥ s = 12.55 s .
t ′f =
+ ⎜ ⎟ +
=⎢
+ ⎜
+
⎝ 9.81 ⎟⎠
g
⎝ g⎠
g
9.81 ⎥
⎢⎣ 9.81
⎦
voy
′
The range for the primed system is given by
(14)
xR′ = vox
′ t f′ = (17.8 )(12.55 ) m = 223 m .
(15)
Therefore,
xR = x ′R + Δx = 223 m + 58 m = 281 m .
(16)
3-6) An Olympic athlete completes a long jump of 8.3 m having pushed off of the board with a
speed of 9.7 m / s . Assuming air resistance is negligible, calculate the following:
a)
b)
c)
The angle, with respect to the horizontal, at which she jumped.
The maximum vertical change of a point on her waistline.
The time of flight. Assume upon landing that her waistline is at the same height
from which she jumped.
y
ttop vo cosθ o

vo
0 = to
m
hmax
θo
tf
xR

ro

vo

a
x
y
0
0
vo cosθ o
vo sin θo
0
−g
S 3-7
x
The equations of motion are, therefore,
v x = vo cos θo ,
v y = v o sin θ o − gt ,
(1)
(2)
x = vo (cos θ o ) t ,
a)
(3)
y = vo ( sin θ o ) t − (1 / 2 ) gt 2 .
We note that when t = t f , y = 0 and equation (4) becomes
(4)
0 = vo ( sinθo )t f − (1 / 2 ) gt 2f .
Equation (5) implies
(1 / 2 ) gt f
(5)
= vo ( sinθo ) .
(6)
Therefore,
⎛ v sinθo ⎞
t f = 2⎜ o
.
⎝
g ⎟⎠
(7)
We also note that x = x R when t = t f . Using equation (7) in equation (3) yields
xR = vo (cosθ o )t f = vo (cos θ o )[ 2vo sin θ o / g ] = vo2 sin 2θ o / g .
(8)
xR g
,
vo2
(9)
Therefore,
sin2θ o =
and
b)
(
−2
1 −1 ⎡ x R g ⎤ 1 −1 ⎡ (8.3 m ) 9.81 m ⋅ s
θ o = sin ⎢ 2 ⎥ = sin ⎢
2
(9.7 m / s )2
⎢⎣
⎣ vo ⎦ 2
By symmetry, we note that
) ⎤⎥ = 30° .
⎥⎦
ttop = t f / 2 = vo sin θ o / g .
(10)
(11)
Equation (11) into equation (4) will give us the maximum height. We have
y = hmax = vo ( sin θo )[vo sin θ o / g ] − (1 / 2 ) g [ vo sinθo / g]
=
c)
(v o sin θ o )
2g
2
((9.7m / s) sin 30°)
=
(
2 9.81 m ⋅ s−2
)
2
2
= 1.20 m .
(12)
Using equation (7)
⎛ v sinθo ⎞ 2 ( 9.7m / s ) sin 30°
t f = 2⎜ o
=
= 0.99 s
⎝
g ⎟⎠
9.81 m ⋅ s −2
(
)
kg and charge q = −e = −1.6 ×10 −19 C is
6
moving horizontally with a speed of vo = 2.4 × 10 m / s when it moves into a region of space
3-7) An electron of mass me = 9.109 ×10
−31
where two horizontal, electrically charged plates generate a uniform vertical electric field, as
represented in the diagram below. The plates are 2 cm in length. The electron experiences a
S 3-8
vertical acceleration of magnitude 4 ×10 m / s directed upward. Calculate the following
quantities of interest:
a)
The time of flight t f for the electron between the plates.
b)
The value of z ; the distance the electron is deflected from its original path while
between the plates.

c)
The velocity v L of the electron as it leaves the region between the plates.
14
d)
2
The angle θ x ; the angle the later velocity vector makes to the positive branch of the
x -axis.

vL
θx
()
Up k̂
z
me
()
x î

vo
−e

E
 = 2 cm
We begin with a table.

ro

vo

a
x
z
0
0
vo
0
0
a
The equations of motion, then, are given by
a)
and
v x = vo ,
vz = at ,
x = vo t ,
z = (1 / 2 ) at 2 .
We note that x =  = 2 cm when t = t f . Therefore, equation (3) becomes
 = vot f ,
(
)
t f =  / vo = (0.02 m) / 2.4 ×10 6 m / s = 8.3 × 10 −9 s ≡ 8.3 ns .
S 3-9
(1)
(2)
(3)
(4)
(5)
(6)
b)
We use equations (4) and (6) to find the value of z at t = t f .
(
)(
)
z f = (1 / 2 ) at 2f = (1 / 2) 4 ×1014 m / s 2 8.3 ×10 −9 s = 0.0139 m ≡ 1.39 cm .(7)
c)
The later velocity is given by

v L = vo î + at ĵ .
So, at t = t f , equation (8) yields
(
)(
)

v L = 2.4 × 10 6 m / s î + 4 ×1014 m / s 2 8.3 × 10 −9 s ˆj

v L = 2.4 î + 3.3 ĵ ×10 6 m / s .
The angle the velocity vector makes to the positive branch of the x-axis is given by
v
⎡ 3.3 ⎤
θ x = tan−1 z = tan−1 ⎢
⎥ = 54.2° .
vx
⎣ 2.4 ⎦
(
d)
(8)
)
(9)
(10)
3-8) A point mass m is thrown from level ground with an initial speed vo at an angle θ o above
the horizontal. Assume air resistance is negligible. Do the following:
(
)2 / (2g ) .
a)
Show that the maximum height is given by: hmax = vo sin θ o
b)
Show that the time of flight is given by: t f = 2vo sin θ o / g .
c)
Describe the physical significance of the term vo sin θ o / g for projectile motion.
d)
e)
Show that the speed with which the point mass strikes the ground v f = v o .
Show that the maximum horizontal range value is given by:
xR = v2o sin 2θ o / g .
y
ttop vo cosθ o

vo
0 = to
m
hmax
θo
tf
xR

ro

vo

a
x
y
0
0
vo cosθ o
vo sin θo
0
−g
x
We have seen this kind of thing before. It is hoped that it will begin to register that all
projectile motion problems have some essentially common elements that one can generalize into a
few equations.
v x = vo cos θo ,
(1)
v y = v o sin θ o − gt ,
x = vo (cos θ o ) t ,
S 3-10
(2)
(3)
a)
y = vo ( sin θ o ) t − (1 / 2 ) gt 2 .
At maximum height, t = ttop and v y = 0 . Equation (2) yields
0 = vo sinθo − gttop .
Therefore,
(4)
(5)
ttop = vo sinθo / g .
(6)
So, y = hmax when t = ttop . Using equations (4) and (6) gives us
2
y = hmax = vo ( sin θo )t top − (1 / 2 ) gt top
= vo ( sin θ o )[ vo sinθ o / g ] − (1 / 2 ) g [vo sin θ o / g ]
2
=
b)
(v o sin θ o )
2g
2
.
(7)
Next, we note that y = 0 when t = t f . So, equation (4) becomes
0 = vo ( sinθo )t f − (1 / 2 ) gt 2f ,
(8)
(1 / 2 ) gt 2f = vo ( sinθo )t f .
and
Therefore,
(9)
t f = 2 ⎡⎣( vo sin θ o ) / g ⎤⎦ = 2t top .
(10)
One might expect this kind of result from symmetry.
c)
I call the time ttop . It is the time the projectile takes to go from its initial height to its
maximum height.
d)
The x-component of speed is the same as the initial x-component of speed; there is no
acceleration parallel to the x-axis to change v x .
v f ,x = vo cosθ o ,
v f ,y = vo sin θ o − gt f
So,
while
Therefore,
(11)
= vo sin θ o − g [ 2v o sin θ o / g ] = −vo sinθo .
(
(12)
)
v 2f = v 2f , x + v2f , y = (v o cosθ o ) + ( −vo sinθo ) = vo2 cos2 θ o + sin 2 θ o = vo2 ,
and
v f = vo .
2
e)
The maximum range is given by
2
(13)
(14)
xR = vo (cosθ o )t f
vo2
v 2o
= vo ( cosθ o ) ⎡⎣ 2 ( vo sin θ o ) / g ⎤⎦ = ( 2 sin θ o cosθ o ) = sin 2θ o .
g
g
S 3-11
(15)
3-9) At time to = 0 , a point mass m is thrown with an initial speed vo at an angle θ o above the
horizontal from a point a vertical distance ho above level ground, as represented in the diagram
below. Assume air resistance is negligible. Derive general equations for the following quantities of
interest:
a)
The maximum height, hmax .
b)
The time of flight t f .
c)
The speed with which the point mass strikes the ground v f .
d)
The angle the final velocity vector makes to the positive branch of the x -axis, θ f .
e)
The maximum horizontal range, xR .
The difference between this problem and the previous is the introduction of an initial height
ho . This change will result in a change in the equations and, of course, increased complexity in the
equations of motion.
()
Up k̂
m

vo
θo
to
hmax
ho
tf
xR

ro

vo

a

vf
x
z
0
ho
vo cosθ o
vo sin θo
0
−g
v x = vo cos θo ,
vz = vo sin θo − gt ,
x = vo (cos θ o ) t ,
a)
z = ho + vo ( sin θ o ) t − (1 / 2 ) gt 2 .
At maximum height, t = ttop and vz = 0 . Equation (2) yields
S 3-12
θf
()
x î
(1)
(2)
(3)
(4)
0 = vo sinθo − gttop .
ttop = vo sinθo / g .
Therefore,
(5)
(6)
So, z = hmax when t = ttop . Using equations (4) and (6) gives us
2
z = hmax = ho + vo ( sinθo )t top − (1 / 2 ) gt top
= ho + vo ( sin θ o )[ vo sin θ o / g ] − (1 / 2) g [vo sin θ o / g ]
2
= ho +
b)
(vo sin θ o )
2
2g
.
(7)
Next, we note that z = 0 when t = t f . So, equation (4) becomes
and
0 = ho + vo (sin θ o ) t f − (1 / 2) gt 2f ,
(8)
⎡ v sinθo ⎤
2h
t 2f − 2 ⎢ o
tf − o = 0 .
⎥
g
⎣ g ⎦
(9)
(It is usually worth the effort to do the algebra necessary to make the coefficient of the quadratic
term equal to one.) The roots, then, are given by
2
⎡ v sinθo ⎤
⎡ v sinθo ⎤ 2ho
tf = ⎢ o
± ⎢ o
⎥
⎥ + g ,
⎣ g ⎦
⎣ g
⎦
(10)
where the minus term is not physically meaningful to this physical state of affairs.
One might expect this kind of result from symmetry.
c)
At time t f , the x-component of the final velocity is the same as the initial x-component; there
being no acceleration parallel to the x-axis to change v x . So,
v f ,x = vo cosθ o .
(11)
The z-component of the final velocity is given by
v f ,z = vo sinθ o − gt f
Therefore,
2
⎡ v sinθ
⎡
v
sin
θ
⎤
2ho ⎤
o
o
o
o
⎢
⎥
= vo sin θ o − g
+ ⎢
+
⎥
g ⎥
⎢ g
⎣ g ⎦
⎣
⎦
2
⎡
⎡ vo sinθo ⎤ 2ho ⎤
⎥ = − (vo sin θ o )2 + 2ho g .
= − ⎢g ⎢
+
⎥
g ⎥
⎢
⎣ g
⎦
⎣
⎦
(12)
v 2f = v 2f , x + v2f , z = vo2 cos 2 θ o + vo2 sin 2 θ o + 2gho ,
and
(
)
v f = vo2 cos2 θ o + sin 2 θ o + 2gho = v2o + 2gho .
S 3-13
(13)
d)
The angle θ f , measured to the positive branch of the x-axis, is given by
⎡ v cos θ
o
θ f = cos ⎢ o2
⎢⎣ vo + 2gho
−1
e)
The maximum range is given by
⎤
⎥.
⎥⎦
(14)
xR = vo (cosθ o )t f
2
⎡ v sinθ
⎡ vo sin θ o ⎤
2ho ⎤
o
o
⎢
⎥
= vo ( cosθ o )
+ ⎢
⎥ + g
g
g
⎢
⎥
⎣
⎦
⎣
⎦
v2o sin θ o cos θ o
v2o sin 2 θ o 2ho 2
2
2
=
+ vo cos θ o
+
vo cos2 θ o
2
g
g
g
2
v2o sin θ o cos θ o
⎛ vo2 sin θ o cos θ o ⎞
2ho 2
v2o sin 2 θ o / g
2
=
+ ⎜
⎟⎠ + g vo cos θ o v2 sin 2 θ / g
g
g
⎝
o
o
2
2
v2o sin θ o cos θ o
⎛ vo2 sin θ o cos θ o ⎞ ⎛ v2o sin θ o cos θ o ⎞
2ho
=
+ ⎜
+
2
⎟⎠ ⎜⎝
⎟⎠ v sin2 θ / g
g
g
g
⎝
o
o
⎡
2ho g ⎤
⎢1 + 1 + 2 2 ⎥
v o sin θ o ⎦
⎣
v2o sin 2θo ⎡
2ho g ⎤
=
⎢1 + 1 + 2 2 ⎥ .
2g
vo sin θ o ⎦
⎣
v2o sin θ o cos θ o
=
g
(15)
3-10) Find the magnitude of the radial (centripetal) acceleration of the following:
a)
A point at the equator of the Earth. (You may ignore the Earth’s orbital motion.)
b)
The Earth in its orbit of the Sun. (Treat the orbit as circular.)
c)
The Sun in its orbit of the center of the Milky Way Galaxy. (Treat the orbit as
20
8
circular with a radius of 3 ×10 m and the Sun’s orbital period is 2 × 10 yrs .
We recall that the magnitude of the radial acceleration is given by
arad = v 2 / R = Rω 2 ,
where v and ω are the tangential and angular speeds, respectively.
a)
2
arad
⎛ 2π rad ⎞
6
= R⊕ ⎜
= 6.371 × 10 m
⎟
⎝ τ
⎠
(
rot
b)
arad = r⊕
)
4π 2
( 24 ( 3,600 s))
2
= 3.37 ×10
−2
m
.
s2
4π 2
4π 2
11
−3 m
=
1.496
×10
m
=
5.9
×
10
.
2
τ orb
s2
( 365 ( 24 )( 3600 s))2
(
)
S 3-14
(1)
(2)
c)
arad = rgal
4π 2
4π 2
20
−10 m
= 3 × 10 m
= 3 × 10
. (3)
2
2
τ gal
s2
⎡⎣ 2 ×10 8 ( 365 ( 24 )( 3600 s ))⎤⎦
(
)
3-11) a) The speed of an electron in an hydrogen atom is v = 2.2 × 10 m / s and its orbital
−11
radius is R = 5.3 × 10 m ; we model the orbit as circular. Calculate the magnitude of the
electron’s radial acceleration. b) A neutron star has an equatorial radius R = 20 km and is
observed to rotate once every second. Calculate the radial acceleration of a point on the equator of
the star.
(a)
(b)
6

arad
−e
R
e

arad

v
R
a)
arad
b)
arad
(
2.2 ×10 6 m / s
v2
=
=
R
5.3 × 10−11 m
)
2
= 9.1 × 10 m / s .
22
2
4π 2
4π 2
3
5
2
= Rω = R 2 = 20 ×10 m
2 = 7.9 × 10 m / s .
τ
(1 s )
(
2
)
(1)
(2)
3-12)
m

v
R
R⊕
M⊕
A geosynchronous satellite is one which appears to be fixed in the sky. The orbit is circular
7
and has a radius of R = 4.2 ×10 m . Calculate the magnitude of its radial acceleration relative
to the Earth’s center.
S 3-15
arad
4π 2
4π 2
7
2
= Rω = R 2 = 4.2 × 10 m
2 = 0.22 m / s .
τ
(24 ( 3,600 s))
(
2
)
(1)
3-13) Two balls are thrown from the top of a cliff with equal initial speeds vo . One is thrown at
an angle θ o above the horizontal and the other at an angle θ o below the horizontal. Show that the
(
)
difference in their range values is vo sin 2θ o / g .

v1
0 = to
m
2
θo
θo

v2

xR1 − x R2

Table for v1
x

ro,1
0

vo ,1 vo cos θ o

a1
0

The range for v1 is given by
y
ho
vo sin θ o
−g

ro,2

vo ,2

a2
x
y
0
ho
vo cosθ o
−vo sin θ o
0
−g
xR1 = v o ( cosθ o ) t f1 ,
(1)
xR2 = v o ( cosθ o ) t f2 .
(2)
xR1 − x R2 = vo (cos θo )t f1 − vo (cos θ o ) t f 2 = vo cos θ o ⎡⎣ t f1 − t f2 ⎤⎦ .
(3)

while the range for v2 is given by
Therefore,
Table for v2
We have seen that in general,
2
v sin θ o
⎡ v sinθo ⎤ 2ho
tf = o
+ ⎢ o
⎥ + g .
g
⎣ g
⎦
So, equation (4) represents time t f1 while t f2 is given by
v sin ( −θ o )
⎡ v sin (−θo ) ⎤ 2ho
t f2 = o
+ ⎢ o
⎥ +
g
g
g
⎣
⎦
2
S 3-16
(4)
2
v sin θ o
⎡ v sin θ o ⎤ 2ho
=− o
+ ⎢ o
⎥ + g .
g
⎣ g
⎦
(5)
Therefore, equation (3) becomes
xR1 − x R2 = vo cos θ o ⎡⎣ t f1 − t f2 ⎤⎦
2
⎡ v sin θ
⎡ vo sin θ o ⎤ 2ho
o
o
= vo cosθ o ⎢
+ ⎢
⎥ + g
⎢ g
⎣ g
⎦
⎣
⎛ v sin θ
o
− ⎜− o
+
g
⎜⎝
2
⎡ vo sin θ o ⎤
2ho ⎞ ⎤⎥
⎢
⎥ + g ⎟⎟ ⎥
⎣ g ⎦
⎠⎦
⎛ 2vo sin θ o ⎞ v2o
= vo cosθ o ⎜
⎟⎠ = g sin 2θ o .
⎝
g
3-14)
(6)
y 
vo
θo
0 = to
m
2R
tf
R
x
A ball is thrown with an initial speed vo at an angle θ o above the horizontal from the top of a
building of h = 2R . It lands at a distance R from the base. Show that
R=
Our equations of motion are
and
2v2o cos2 θ o ( 2 + tan θ o )
g
.
x = vo (cos θ o ) t ,
y = 2R + vo (sin θ o ) t − (1 / 2) gt .
2
(1)
(2)
When t = t f , x = R and equation (1) yields
R = vo (cos θ o ) t f → t f = R / vo (cosθ o ) .
Next, we note that y = 0 when t = t f . Equations (3) and (2) combine to give us
S 3-17
(3)
2
⎡
⎤
⎡
⎤
R
R
0 = 2R + vo ( sin θo ) ⎢
⎥ − (1 / 2 ) g ⎢
⎥ ,
v
cos
θ
v
cos
θ
(
)
(
)
o
o
o
o
⎣
⎦
⎣
⎦
and
R2
0 = 2R + R tanθ o − 2
.
2vo cos 2 θ o
Solving for R , we find
R=
2v2o cos2 θ o ( 2 + tan θ o )
g
(4)
(5)
.
(6)
3-15) A projectile of mass m is fired up an inclined plane with an initial speed vo at an angle θ
to the horizontal, as represented in the diagram below. Air resistance is negligible.
y
tf

vo
m
a)
( cos ϕ , sin ϕ )
ϕ
θ

x
If the angle of the incline is ϕ with respect to the horizontal, show that the range
along the incline is given by
b)
2vo2 sin (θ − ϕ ) cosθ
=
.
g cos2 ϕ
Use the trigonometric identity for sin A cos B to get the maximum distance
vo2
 max =
.
g (1 + sin ϕ )
c)
If the projectile is fired down the incline instead, show that the maximum distance is
.  max
vo2
=
.
g (1 − sin ϕ )
We begin by setting up a table. We can write

ro

vo ,1

a1
x
y
0
0
vo cos θ o
vo sin θ o
0
−g
,
which gives us the following equations of motion:
and
x = vo (cos θ )t ,
y = vo ( sin θ ) t − (1 / 2 ) gt 2 .
S 3-18
(1)
(2)
At time t = t f , we have x =  cosϕ . Using these conditions, equation (1) becomes
a)
x =  cosϕ = vo ( cosθ ) t f ,
cos ϕ
tf =
.
vo (cosθ )
and, therefore,
(3)
(4)
Substitution of equation (4) into equation (2) yields
2
⎛  cos ϕ ⎞
⎛  cos ϕ ⎞
(
)
 sin ϕ = vo ( sin θ )⎜
−
1
/
2
g
⎜⎝ v ( cosθ ) ⎟⎠ .
⎝ v (cos θ )⎟⎠
o
Equation (5) implies
and
b)
(5)
o
 2 g cos2 ϕ
 sin ϕ =  tanθ cos ϕ − (1 / 2 ) 2
,
vo cos 2 θ
vo2 cos2 θ
vo2 cosθ
 = 2 (tan θ cos ϕ − sin ϕ )
= 2 (sin θ cos ϕ − cosθ sin ϕ )
g cos 2 ϕ
g cos 2 ϕ
2vo2 sin (θ − ϕ ) cosθ
=
.
g cos2 ϕ
(6)
(7)
Using the trigonometric identity
sin A cos B =
we can write equation (7) as
1
⎡⎣ sin ( A + B ) + sin ( A − B )⎤⎦ ’
2
(8)
vo2
=
⎡ sin ( 2θ − ϕ ) − sin ϕ ⎤⎦ .
(9)
g cos2 ϕ ⎣
From equation (7), it is obvious that at θ = ϕ ,  would be a minimum. So, to find a candidate for
a maximum value, we take the derivative of equation (9) with respect to θ and set it equal to zero.
To that end, we write
d
vo2
d
vo2
=
⎡ sin ( 2θ − ϕ ) − sin ϕ ⎤⎦ =
2 cos ( 2θ − ϕ ) = 0 .
dθ g cos2 ϕ dθ ⎣
g cos2 ϕ
(10)
Equation (10) requires
cos −1 ⎡⎣ cos ( 2θ − ϕ )⎤⎦ = 2θ − ϕ = cos−1 [ 0 ] = π / 2 .
Substitution of equation (11) into equation (9) gives us
 max
c)
(11)
⎤
vo2 ⎡ sin (π / 2 ) − sin ϕ ⎤ v2o ⎡ 1− sin ϕ ⎤ vo2 ⎡
1 − sin ϕ
= ⎢
=
=
⎥ g ⎢ 1 − sin 2 ϕ ⎥ g ⎢ (1− sin ϕ )(1 + sin ϕ ) ⎥
g ⎣
cos2 ϕ
⎦
⎣
⎦
⎣
⎦
2
vo
=
.
(12)
g (1+ sin ϕ )
For a projectile fired down the incline, we have
S 3-19
y

vo
x
ϕ
tf
( cos ϕ ,− sin ϕ )
θ
m

and
2
⎛  cos ϕ ⎞
⎛ cos ϕ ⎞
(
)
− sin ϕ = vo (sin θ ) ⎜
−
1
/
2
g
⎜⎝ v ( cosθ ) ⎟⎠ .
⎝ v ( cosθ ) ⎟⎠
o
(13)
o
Therefore,
vo2 cos2 θ
vo2 cosθ
 = 2 (tan θ cos ϕ + sin ϕ )
= 2 (sin θ cos ϕ + cosθ sin ϕ )
g cos 2 ϕ
g cos 2 ϕ
2vo2 sin (θ + ϕ ) cosθ
vo2
=
=
⎡⎣ sin (2θ + ϕ ) + sin ϕ ⎤⎦ .
g cos2 ϕ
g cos 2 ϕ
(14)
Taking the derivative, we find
d
vo2
d
vo2
d
=
⎡⎣ sin ( 2θ + ϕ ) + sin ϕ ⎤⎦ =
⎡ −2cos ( 2θ + ϕ )⎤⎦ = 0 . (15)
2
2
dθ g cos ϕ dθ
g cos ϕ dθ ⎣
So,
cos −1 ⎡⎣ cos ( 2θ + ϕ )⎤⎦ = 2θ + ϕ = cos−1 [ 0 ] = π / 2 .
(16)
Therefore,
⎤
vo2 ⎡ sin (π / 2 ) + sin ϕ ⎤ v2o ⎡
1+ sin ϕ
vo2
 max = ⎢
⎥ = g ⎢ (1 + sin ϕ ) (1 − sin ϕ ) ⎥ = g (1 − sin ϕ ) .
g ⎣
cos2 ϕ
⎦
⎣
⎦
3-17) The position of a particle of mass m is given by

r = Ao cos (ωt ) î + Ao sin (ω t ) ĵ ,
where Ao and ω are constants. Do the following:
a)
(17)
a)
Find the magnitude of the position vector.
b)
Describe the shape of the path of point mass m .
c)
Derive expressions for the velocity and the acceleration of the point mass.
 

d)
Find r , v and a if Ao = 1.0 m and ω = π / 10 rad / s .
The magnitude is given by

r =r=
(A
o
(
)
cos (ω t )) + ( Ao sin (ωt )) = Ao2 cos 2 (ω t ) + sin2 (ωt ) = Ao .
2
b) The shape of the path is circular.
c) The instantaneous velocity is given by
2
S 3-20
(1)
(
)
 d
v = ⎡⎣ Ao cos (ωt ) î + sin (ω t ) ĵ ⎤⎦ = Ao ⎡⎣ −ω sin (ω t ) î + ω cos (ω t ) ĵ ⎤⎦
dt
= Aoω ⎡⎣ − sin (ω t ) î + cos (ω t ) ĵ ⎤⎦ .
The acceleration is given by
{
}
 d
a=
Aoω ⎡⎣ − sin (ω t ) î + cos (ω t ) ĵ ⎤⎦
dt
= −A oω 2 ⎡⎣ cos (ωt ) î + sin (ω t ) ĵ ⎤⎦ .
d)
and
(2)
(3)
⎛ ⎛ π −1 ⎞ ⎞
⎛ ⎛ π −1 ⎞ ⎞ ⎤

⎛ π rad ⎞ ⎡
v = (1.0 m ) ⎜
− sin ⎜ ⎜ s ⎟ t ⎟ î + cos ⎜ ⎜ s ⎟ t ⎟ ĵ ⎥
⎟
⎢
⎝ 10 s ⎠ ⎣
⎝ ⎝ 10 ⎠ ⎠
⎝ ⎝ 10 ⎠ ⎠ ⎦
⎛ ⎛ π −1 ⎞ ⎞
⎛ ⎛ π −1 ⎞ ⎞ ⎤
⎛ π m⎞ ⎡
=⎜
−
sin
s
t
î
+
cos
⎜⎝ ⎜⎝ 10 ⎟⎠ ⎟⎠
⎜⎝ ⎜⎝ 10 s ⎟⎠ t ⎟⎠ ĵ ⎥ ,
⎝ 10 s ⎟⎠ ⎢⎣
⎦
(4)
⎛⎛ π
⎛⎛ π

⎛ π rad ⎞ ⎡
⎞ ⎞
⎞ ⎞ ⎤
a = − (1.0m ) ⎜
cos ⎜ ⎜ s −1 ⎟ t ⎟ î + sin ⎜ ⎜ s−1 ⎟ t ⎟ ĵ ⎥
⎟
⎢
⎝ 10 s ⎠ ⎣
⎝ ⎝ 10 ⎠ ⎠
⎝ ⎝ 10 ⎠ ⎠ ⎦
2
2
3-18)
⎛ π 2 m ⎞ ⎡ ⎛ ⎛ π −1 ⎞ ⎞
⎛ ⎛ π −1 ⎞ ⎞ ˆ ⎤
= −⎜
cos
s
t
î
+
sin
⎢
⎜
⎟
⎜⎝ ⎜⎝ 10 s ⎟⎠ t ⎟⎠ j ⎥ .
⎝ 100 s 2 ⎟⎠ ⎣ ⎜⎝ ⎝ 10 ⎠ ⎟⎠
⎦
(5)
y

vo
to = 0
m
θ = 10°
x
ϕ = 20°

tf
A skier takes off at a speed of 108 km / hr at an angle θ o = 10° above the horizontal, as
represented in the diagram above. Calculate the distance  along a 20° slope she goes before she
lands.
By now, you too may be able to write down the equations of motion for constant acceleration
without the need for a table. We have
v x = vo cos θo ,
(1)
v y = v o sin θ o − gt ,
S 3-21
(2)
x = vo (cos θ o ) t ,
(3)
y = vo ( sin θ o ) t − (1 / 2 ) gt 2 .
(4)
We note first that at time t = t f , x =  cosϕ and y = − sin ϕ . So, equation (3) becomes
 cos ϕ = vo (cos θo )t f ,
 cos ϕ
tf =
.
vo (cosθ o )
which implies
(5)
Equation (5) into an appropriate equation (4) yields
2
⎡  cos ϕ ⎤
⎡  cosϕ ⎤
− sin ϕ = vo (sin θ o ) ⎢
⎥ − (1 / 2 ) g ⎢
⎥ .
v
cos
θ
v
cos
θ
(
)
(
)
o
o
o
o
⎣
⎦
⎣
⎦
(6)
After some algebra, we can write
g cos2 ϕ
⎡ sin θ o cos ϕ
⎤
=
2
+
sin
ϕ
⎢
⎥,
vo2
⎣ cosθ o
⎦
2
2vo
⎡ cosθ o ( sinθo cos ϕ + cosθ o sin ϕ )⎤⎦
=
g cos2 ϕ ⎣
2vo2
⎡ sin (θ o + ϕ ) cosθ o ⎤⎦
=
g cos2 ϕ ⎣
and
2 (108 (1000 m ) / ( 3600 s ))
2
=
(9.81 m / s ) cos
2
2
20°
⎡⎣ sin (10° + 20° ) cos10° ⎤⎦ = 102.3 m .
(7)
(8)
3-19)
θo
0 = to

vo
x
h

tf
y
A car is out of control and moving with a speed of vo when it slides off of a steep embankment of
height h at an angle θ o to the horizontal, as represented in the diagram below. The car lands a
distance  from the base. Show that the speed with which the car left the embankment is given by
vo =

cosθ o
g
.
2 ( h −  tanθ o )
S 3-22
Our equations of motion are given by
x = vo (cos θ o ) t ,
(1)
y = vo ( sin θ o ) t + (1 / 2 ) gt 2 .
We note that at time t = t f , x =  and y = h . So, equation (1) gives us
and
(2)
 = vo (cos θo )t f ,

tf =
.
vo cos θo
which implies
(3)
(4)
Equation (4) into an appropriate equation (2) yields
2
⎛
⎞
⎛

 ⎞
(
)
h = vo ( sinθo )⎜
+
1
/
2
g
⎜⎝ v cosθ ⎟⎠ ,
⎝ vo cos θ o ⎟⎠
o
o
(5)
g 2
h = tan θ o + 2
.
2vo cos2 θ o
(6)
2
g
v =
.
2
cos θ o 2 ( h −  tan θ o )
(7)
and
After more algebra, we have
2
o
Therefore, then,
vo =

cosθ o
g
.
2 ( h −  tanθ o )
S 3-23
(8)
Solutions to Problems for Chapter Four
−10
4-1) A molecule of HCl is represented in the diagram below. where  = 1.3 × 10 m where the
mass of hydrogen and chlorine are, respectively, mCl = 35mH = 35 u and the atomic mass unit
is u = 1.661 × 10
molecule.
−27
kg . With respect to the hydrogen atom, calculate the center of mass of this
y
mH
x
mCl

We can write
⎡ m H ( 0 ) + mCl ( ) ⎤
⎡ mCl
⎤
⎡ 35mH
⎤

rcm = ⎢
⎥ î = ⎢
⎥  î = ⎢
⎥  î
m
+
m
m
+
m
m
+
35m
⎣
H
Cl
⎦
⎣ H
Cl ⎦
⎣ H
H ⎦
⎡ 35 ⎤
⎡ 35 ⎤
−10
−10
= ⎢ ⎥  î = ⎢ ⎥ 1.3 ×10 m î = 1.26 × 10 m ≡ 0.126 nm .
(1)
⎣ 36 ⎦
⎣ 36 ⎦
4-2) A water molecule, H 2 O , is represented in the diagram below, where the distance from the
(
)
−10
center of the oxygen atom to center of each hydrogen atom is given by  = 10 m . The masses
−27
are related by mO = 16m H = 16 u , where the atomic mass unit is u = 1.661 × 10 kg . With
respect to the oxygen, calculate the center of mass of this molecule. Assume the x-axis bisects the
105° angle.
y
mO
mH
105°
x

mH
By symmetry, we can write
⎡ mO (0 ) + 2mH ( cos (105° / 2 )) ⎤
⎡ 2mH (cos (105° / 2 )) ⎤

rcm = ⎢
⎥ î = ⎢
⎥  î
m
+
2m
m
+
2m
O
H
O
H
⎣
⎦
⎣
⎦
⎡ 2mH (cos (105° / 2 )) ⎤
⎡ ( cos (105° / 2 )) ⎤ −10
=⎢
 î
=
⎥
⎢
⎥ 10 m î = 6.76 pm î . (1)
16m
+
2m
9
H
H
⎣
⎦
⎣
⎦
(
S 4-1
)
4-3) A uniform square of side length 2R has a circular hole of radius R / 2 removed, as
represented in the diagram below. Find the center of mass relative to the center of the original
square. The center of the hole has coordinates ( R / 2, R / 2 ) . (Hint: treat the hole as having
negative mass.)
y
m
R/ 2
2R
x
M
The mass of the original square is given by
M = σ Aarea = σ (2R ) = 4σ R 2 ,
(1)
m = − σ Aarea = − σπ ( R / 2 ) = − σπ R 2 / 4 .
(2)
2
where σ signifies the uniform surface mass density. The mass of the hole is given by
2
So, we have
⎡ M ( 0 ) + m ( R / 2 )⎤⎦ î + ⎡⎣ M ( 0) + m ( R / 2 )⎤⎦ ĵ

rcm = ⎣
M +m
R ⎡⎛ m ⎞
⎛ m ⎞ ⎤
= ⎢⎜
î
+
⎟
⎜⎝
⎟ ĵ
2 ⎣⎝ M + m ⎠
M + m ⎠ ⎥⎦
R ⎡ ⎛ − σπ R 2 / 4
⎞
⎛
− σπ R 2 / 4
⎞ ⎤
= ⎢⎜
î
+
⎜⎝ 4σ R 2 − σπ R 2 / 4 ⎟⎠ ĵ ⎥
2 ⎣ ⎝ 4σ R 2 − σπ R 2 / 4 ⎟⎠
⎦
⎛ ⎛ − (π / 4 ) ⎞ ⎞ ˆ ⎤
R ⎡ ⎛ − (π / 4 ) ⎞
= ⎢⎜
î + ⎜ ⎜
(3)
⎟ j ⎥ =− 0.122 î − 0.122 ĵ .
2 ⎢⎣ ⎝ 4− (π / 4 )⎟⎠
⎝ ⎝ 4 − (π / 4 ) ⎟⎠ ⎠ ⎥⎦
4-4) A uniform disk of radius R has a circular hole of radius R / 2 removed, as represented in
the diagram below. Find the center of mass relative to the center of the original disk. (Hint: treat
the hole as having negative mass.)
The mass of the original disk is given by
M = σ Aarea = σ (π R ) = σπ R 2 ,
(1)
m = − σ Aarea = − σπ ( R / 2 ) = − σπ R 2 / 4 .
(2)
2
where σ signifies the uniform surface mass density. The mass of the hole is given by
2
So, by symmetry, we have
⎡ M ( 0) + m( R / 2) ⎤
R⎡ m ⎤
R ⎡ − σπ R 2 / 4
⎤

rcm = ⎢
î
=
î
=
î
⎥
M +m
2 ⎢⎣ M + m ⎥⎦
2 ⎢⎣ σπ R 2 − σπ R 2 / 4 ⎥⎦
⎣
⎦
S 4-2
=
R ⎡ − (1 / 4 ) ⎤
î = − 0.16 R î .
2 ⎢⎣ 1− (1 / 4 ) ⎥⎦
(3)
y
R/ 2
R
x
m
M
4-5) A uniform sphere of radius R has a spherical hole of radius a removed. The center of the
hole is a distance r from the center of the sphere, as represented in the diagram below. Find the
center of mass. (Hint: treat the hole as having negative mass.)
y
a
m
r
R
x
M
The mass of the original sphere is given by
(
)
M = ρVolume = ρ ( 4π / 3) R 3 ,
where ρ signifies the uniform volume mass density. The mass of the hole is given by
(
)
m = − ρVolume = −ρ ( 4π / 3) a 3 .
(1)
(2)
So, by symmetry, we have
⎡ M ( 0 ) + m ( r) ⎤

⎡ m ⎤
rcm = ⎢
î
=
⎥
⎢⎣ M + m ⎥⎦ r î
⎣ M +m ⎦
⎡
⎤
−ρ ( 4π / 3) a 3
⎡ a3 ⎤
=⎢
⎥ r î = − ⎢ 3
3 ⎥ r î .
3
3
R
−
a
ρ
4
π
/
3
R
−
ρ
4
π
/
3
a
(
)
(
)
⎢⎣
⎥⎦
⎣
⎦
(
(
) (
)
)
S 4-3
(3)
4-6) A uniformly thin rod is bent into the shape of an equilateral triangle, as represented in the
diagram below. Calculate the center of mass of this triangle.
y
m


m
x
m

The mass of each side is given by
m = λ ,
(1)
where λ signifies the uniform linear mass density. (By symmetry, it appears that the x-component

of the center of mass should be at rcm,x =  / 2 î . Let us calculate to see.) We can write
m ((  / 2 ) cos60°) + m (  / 2 ) + m (  − ( / 2 ) cos 60°)

rcm,x =
î
3m

(cos 60° + 3 − cos 60°) 
=
î = î .
3
2
2
(2)
For the y-component, we write
m ((  / 2 ) sin 60°) + m (0 ) + m ((  / 2 ) sin 60°)

rcm,y =
î
3m
( sin 60°)
3

rcm,y =
 ĵ =
 ĵ .
3
6
(3)
4-7) A uniformly thin rod is bent into the shape of an isosceles right triangle, as represented in the
diagram below. Calculate the center of mass of this triangle.
y
m
 2

m′
45° = θ
m

S 4-4
x
The mass of each leg is given by
m = λ ,
(1)
( )
(2)
where λ signifies the uniform linear mass density. The mass of the hypotenuse is given by
m′ = λ  2 = m 2 .
For the x-component of the center of mass we can write
( ((
)
))
))  î = 1 + 2 ( 2 − (
2 cos 45°
m ( 0 ) + m (  / 2 ) + m ′  −  2 / 2 (cos 45°)

rcm,x =
î
2m + m ′
=
( (
m + m′ 2 −
2 cos 45°
2m + m ′
2
1+ 2
=
(
2 2+ 2
2+ 2
)
 î =
2
î .
4
((
)
For the y-component, we write
))  î
2
(2)
)
m (  / 2 ) + m ( 0 ) + m ′  2 / 2 sin 45°

rcm,y =
î
2m + m ′
=
m + m′
(( 2 ) sin 45°)  î = 1 + 2 (( 2 )(
2m + m ′
=
(
2 2+ 2
2
1+ 2
(
2 2+ 2
)
 î =
2 /2
)
))  î
2
î .
4
(3)
4-8) Find the center of mass of a uniform hollow cone of of height h and circular base of radius
a as represented in the diagram below. All of the mass is uniformly “smeared” on the lateral
surface of the cone.
z
θ
h
d
θ dz
ϕ
r⊥ d
r⊥
d dA
z
M
a
x
S 4-5
Where to begin. Note that as the mass is uniformly “smeared” on the lateral surface of the
cone, we can write
dM = σ dA ,
(1)
where σ is the uniform surface mass density, and dA is an infinitesimal area on the lateral surface
of the cone and given by
dA = r⊥ dϕ d .
(2)
We note also that
d cosθ = dz ,
(3)
which implies
dz
d =
=
cosθ
using
h2 + a2
s
dz = dz ,
h
h
(4)
s = h2 + a2 ,
(5)
r⊥ h − z
=
,
a
h
(6)
the so-called slant height, though it would seem to this author, slant distance would be more
descriptive.
We also note that
therefore,
r⊥ =
We can now rewrite equation (2) as
a
(h − z ) .
h
(7)
⎛a
⎞
⎛ s ⎞ sa
dA = ⎜ ( h − z )⎟ dϕ ⎜ dz ⎟ = 2 dϕ (h − z ) dz .
⎝h
⎠
⎝h ⎠ h
(8)
We can now calculate the lateral surface area of the cone. We have
sa
ALS = ∫ dA = 2
h
2π
h
0
0
∫ dϕ ∫ (h − z ) dz
h
=
sa
1 2⎤
sa
⎡
⎡1 2 ⎤
2
2
2
π
hz
−
z
=
2
π
h ⎥ = π sa = π a h + a .
[
]
[
]
2
2
⎢
⎥
⎢
h
2 ⎦0 h
⎣
⎣2 ⎦
We now know the mass:
M = σπ sa .
(9)
(10)
By symmetry, we know the x and y coordinates of the center of mass must be zero. So,


M rcm ,z = ∫ rdM ,z dM =
=
∫(
∫ ( z k̂ )σ dA
⎛ sa
⎞ σ sa
z k̂ σ ⎜ 2 dϕ ( h − z ) dz ⎟ = 2
⎝h
⎠
h
)
2π
h
∫ dϕ ∫ (hz − z ) dz k̂
2
0
0
h
=
σ sa
1


⎡1 2 1 3⎤
2
π
hz
−
z
k̂
=
σπ
sah k̂
=
M
r
=
σπ
sa r
[
]
cm
,z
cm ,z .
⎢2
h2
3 ⎥⎦ 0
3
⎣
S 4-6
(11)
Therefore,
1

rcm,z = h k̂ .
3
(12)
4-9) A particle of mass m is moving east with a speed 3u . At the same time, a second particle of
mass 4m is moving west with a speed 2u , as represented in the diagram below. a) Calculate the
velocity of the center of mass of the two mass system. b) Calculate the velocity of the center of
mass of this system if the second particle is moving east also.
y
4m
m
2u
3u
x
We know that for discrete masses,
N

rcm =

∑m r
i i
i=1
N
∑m
i
1
=
M tot
N

∑m r
i i
,
(1)
i=1
i=1
and, therefore,

drcm
1 d N 
1

vcm =
=
mi ri =
∑
dt
M tot dt i=1
M tot
a)
b)

dri
1
∑ mi dt = M
i=1
tot
N
1

∑ mi v i = M
i=1
tot
N
N

∑p
i
. (2)
i=1
If we assign east as î , we can write
We have
3mu î − 8mu î

vcm =
= −u î .
m + 4m
(3)
3mu î + 8mu î 11

vcm =
= u î .
m + 4m
5
(4)
S 4-6
Solutions to Problems for Chapter Five
−2
5-1) Calculate the mass of a body that weighs 2 N at a point in space where g = 9.81 m ⋅ s .
The weight is given by
W = mg ,
(1)
and, therefore,
m=
W
2 N
=
= 0.204 kg .
g 9.81 m ⋅ s −2
(2)
5-2) Calculate the distance from the center of the Earth at which a standard kilogram would
weight one Newton.
This would require
g=
Therefore,
(6.67 ×10
W 1 N GM ⊕
=
= 2 .
m 1 kg
r
)(
(1)
)
N ⋅ m2 ⋅ kg−2 5.97 ×10 24 kg (1 kg/1 N ) = 1.995 × 107 m .
5-3) A constant horizontal force of 40 N acts on a body of mass m that is on a smooth,
r=
−11
(2)
horizontal surface. The body was at rest when the force was initiated. The body is observed to
move 100 m in 5 s . Do the following:
a)
Calculate the mass of the object.
b)
If the force is removed after the 5 s , calculate the distance the body will move in the
next 5 s .
a) As the acceleration is constant, and the initial speed was zero, we have
d = (1 / 2) (F / m ) t 2 ,
(1)
So,
b)
m = (1 / 2 ) (F / d ) t 2 = (1 / 2 )[40 N/100 m ](5 s ) = 5 kg .
2
We have, if there is no acceleration,
(2)
d = vot = [at ′ ]t = ( F / m )tt ′ = ( 40 N/5 kg )( 5 s ) (5 s ) = 200 m . (3)
5-4) A hockey puck leaves a player’s stick with a speed of 10 m / s and slides a distance of
40 m before coming to rest. Calculate the coefficient of kinetic friction between the puck and the
ice.
A free-body diagram may help.
ĵ

v
N
î
fk
mg
Summing forces in the y direction, we find
S 5-1
N − mg = may = 0 ,
N = mg .
(1)
− fk = ma = − µk N = −µ k mg ,
a
µk = − .
g
(3)
and
Summing forces in the x direction gives us
and
(2)
(4)
We also know that for constant acceleration,
v 2 = vo2 + 2a ( Δx ) = 0 .
v 2o
a=−
.
2 ( Δx )
Therefore,
(5)
(6)
Substitution of equation (6) into equation (4) yields
⎡⎣ −vo2 / 2 ( Δx) ⎤⎦
µk = −
= v2o / 2g (Δx )
g
(10 m / s )2
=
= 0.127
2 (9.81 m ⋅ s −2 ) (40 m )
5-5) An electron of mass me = 9.1 ×10
.
(7)
−31
kg leaves the cathode of a radio tube with negligible
6
speed and travels in a straight path to the anode 1 cm away where is has a speed 6 × 10 m / s .
Assuming a constant electrical force and field, define an appropriate coordinate system and do the
following:

a)
Calculate a , the acceleration of the electron.
b)
Calculate t f , the so-called “time of flight.”
c)
E
Calculate F , the electric force exerted on the electron.
A free-body diagram may help.
ĵ
me
î

FE
1 cm
to = vo = 0
a)
t; v
For constant acceleration and an initial speed of zero, we have
v 2 = 0 + 2a ( Δx) ,
and, therefore,

a=
(
)
(1)
2
6 ×10 6 m / s
v2
15
2
î =
î = 1.80 × 10 m / s î .
2 ( Δx)
2 ( 0.01 m )
S 5-2
(2)
b)
The time of flight would be given by
(
v f = at f ,
) (
(3)
)
t f = v f / a = 6 × 106 m / s / 1.8 × 1015 m / s2 = 3.33 ns .
(4)


F E = me a = 9.1 ×10 −31 kg 1.80 ×1015 m / s 2 = 1.64 × 10 −15 N .
(5)
and,
c) We have
(
)(
)
5-6) At some time t , the center of the Moon is a distance r = 3.8 × 10 m ≡ 59.65 R⊕ from the
center of the Earth, as represented in the diagram below. The mass of the Moon is measured to be
M M = 7.36 × 1022 kg . Calculate the magnitude of the gravitational force exerted by the Moon
8
on the three blocks shown if m1 = m2 = m3 = 1 kg . (We model the Moon and the Earth as
spheres. They are not quite spherical. Because of their rotation, they are slightly oblate.)

F3G

F2G

F1G
MM
m3
m1
m2
M⊕
r
For mass one, we have
F1 =
G
(
GM M m1
=
GM M m1
=
GM M m1
(r − R⊕ )2 (aR⊕ − R⊕ )2 ((a − 1) R⊕ )2
)(
)
⎡ 6.67 × 10−11 N ⋅ m 2 ⋅ kg −2 7.36 × 10 22 kg (1kg ) ⎤
⎥ = 3.52 × 10 −5 N .
=⎢
2
⎢
⎥
(59.65 − 1) 6.371 × 10 6 m
⎣
⎦
(
(
))
(1)
For mass two, we have
F2 =
G
(
GM M m1
(r + R⊕ )
2
=
GM M m1
(aR⊕ + R⊕ )
)(
2
=
GM M m1
( ( a + 1) R )
2
⊕
)
⎡ 6.67 × 10−11 N ⋅ m 2 ⋅ kg −2 7.36 × 10 22 kg (1kg ) ⎤
⎥ = 3.29 × 10 −5 N .
=⎢
2
⎢
⎥
(59.65 + 1) 6.371 × 10 6 m
⎣
⎦
(
(
))
For mass three, we have
F3 =
G
(
GM M m1
r + R⊕
2
2
)
2
=
GM M m1
GM M m1
GM M m1
=
=
r 2 + R⊕2 (aR⊕ )2 + R⊕2
a2 + 1 R⊕2
(
S 5-3
)
(2)
(
)(
)
⎡ 6.67 × 10−11 N ⋅ m 2 ⋅ kg −2 7.36 × 10 22 kg (1kg ) ⎤
⎥ = 3.40 × 10 −5 N .
=⎢
(3)
2
2
6
⎢
⎥
59.65 + 1 6.371 × 10 m
⎣
⎦
5-7) A communications satellite of mass m = 200 kg orbits the center of the Earth on a circular
orbit of radius R = 40,000 km . Do the following:
(
)(
)
a)
b)
Calculate the magnitude of the gravitational force exerted on the satellite by the Earth.
Calculate the ratio of the weight of the satellite in orbit to its weight on the surface of the
Earth.
24
(The mass of the Earth is measured to be M ⊕ = 5.97 × 10 kg and the average radius of the
Earth is R⊕ = 6.371 × 10 m .)
6

v

FSG
R⊕
m
R
M⊕
a)
The force exerted on the satellite by the Earth is given by
b)
(
)(
)
6.67 × 10−11 N ⋅ m 2 ⋅ kg −2 5.97 × 1024 kg (200kg)
GM ⊕ m
F =
=
2
R2
4 ×10 7 m
G
S⊕
(
= 49.8 N .
The ratio is given by
(
(
)
(1)
)
)
2
2
m GM ⊕ / R 2
Worbit
⎛ 6.371 × 106 m ⎞
⎛ R⊕ ⎞
=
=⎜
=⎜
= 0.0254 .
(2)
⎝ R ⎟⎠
Wsurface m GM ⊕ / R⊕2
⎝ 4 ×10 7 m ⎟⎠
5-8) A block of mass 1 kg is on a frictionless surface inclined 37° to the horizontal and
subjected to a horizontal force of 5 N , as represented in the diagram below. Do the following:
draw a free-body diagram with an appropriate coordinate system and calculate the magnitude of the
acceleration of the block parallel to the incline.
ĵ
î
mg
co
s
θ
N
F
θ
mg
s
θ
inθ
mg
S 5-4
θ
Summing forces parallel to the x-axis we find
F cos θ − mg sin θ = ma ,
a = ( F / m ) cosθ − g sinθ
and
(
(1)
)
= ((5 N ) / (1 kg)) cos 37° − 9.81 m ⋅ s −2 sin 37° = −1.91 m / s 2 .
(2)
The negative sign signifies that with respect to the indicated coordinate axis, the acceleration was
2
oppositely directed. Its magnitude, of course, is 1.91 m / s .
5-9) A hot-air balloon of mass M descends with an acceleration of magnitude a . Calculate the
mass of the ballast that must be thrown off if the balloon is to accelerate upwards with the same
magnitude of acceleration.
A free-body diagram may prove helpful.
Fbuoyancy
ĵ
Fbuoyancy
ĵ
( M − m) g
Mg
initial
So, initially,
and
We require
later
Mg − Fbuoyancy = Ma ,
Fbuoyancy = M (g − a ) .
Fbuoyancy − ( M − m ) g = ( M − m ) a .
and
M (g − a ) − ( M − m ) g = ( M − m ) a .
The physics is done and the algebra begins. We find
Mg − Ma − Mg + mg = Ma − ma ,
(1)
(2)
(3)
(4)
(5)
ma + mg = Ma + Ma = m ( g + a ) = 2Ma .
(6)
Therefore,
m = 2Ma / (g + a ) .
(7)
5-10) Two blocks of masses m1 = 5 kg and m2 = 6 kg are attached to opposite ends of a light
and
string. The light string is draped over a frictionless pulley. The blocks are constrained to move on
a frictionless wedge, as represented in the diagram below. Do the following:
a)
Calculate the magnitude of the acceleration of each block.
b)
Calculate the tension in the string.
a) We begin with a free-body diagram, see below, and appropriate coordinates axes. We sum
forces parallel to the frictionless surface angled θ to the horizontal and find
m2 g sin θ − T = m2 a .
(1)
Summing the forces parallel to the other surface we get
S 5-5
T − m1g sin ϕ = m1 a .
(2)
î
N1
T
ϕ
g si
m2
m1 g
T
in ϕ
θ
m2 g
î
nθ
gs
m1
N2
Adding equations one and two will eliminate the tension and give us
m2 g sin θ − m1g sin ϕ = m2 a + m1a .
Therefore,
⎡ m sinθ − m1 sin ϕ ⎤
a=⎢ 2
⎥g
m1 + m2
⎣
⎦
⎡ ( 6 kg ) sin 60° − ( 5 kg ) sin 30° ⎤
m
−2
=⎢
9.81 m
⋅
s
=
2.40 .
⎥
s2
(5 kg ) + ( 6 kg )
⎣
⎦
(
)
(3)
(4)
To find the tension, we can use equation (1) or (2). Using (2) we have
(
)
T = m1 ( g sin ϕ + a ) = ( 5 kg) ⎡⎣ 9.81 m ⋅ s −2 sin 30° + 2.40 m ⋅ s −2 ⎤⎦
(
)
= (5 kg ) ⎡⎣ 9.81 m ⋅ s−2 sin 30° + 2.40 m ⋅ s −2 ⎤⎦ = 36.5 N .
Equation (1) yields
(
)
T = m2 ( g sin θ − a ) = (6 kg) ⎡⎣ 9.81 m ⋅ s−2 sin 60° − 2.40 m ⋅ s −2 ⎤⎦ = 36.6 N .
(5)
(6)
5-11)
Two blocks, m1 and m2 , hang one under the other from strings, as represented in the
diagram below. Draw free-body diagrams for each block. Use Newton’s second law to do the
following:
a)
Derive a general equation for T2 , the tension in the lower string.
b)
a)
b)
Derive a general equation for T1 , the tension in the upper string.
c)
If m1 = 2 kg and m2 = 3 kg , calculate the values of T2 and T1 .
For block two, we have
m2 g − T2 = m2 a2 = 0 → T2 = m2 g .
For block one, we have
(1)
m1 g + T2 − T1 = m1 a1 = 0 → T1 = m1g + T2 = m1 g + m2 g = (m1 + m2 ) g . (2)
c) If m1 = 2 kg and m2 = 3 kg , then the tension in the string holding up block two is
(
)
T2 = m2 g = ( 3 kg ) 9.81 m ⋅ s −2 = 29.4 N .
S 5-6
(3)
For string one,
(
)
T1 = (m1 + m2 ) g = (2 kg + 3 kg) 9.81 m ⋅ s −2 = 49.1 N .
T1
T2
T1
m2
m1
(4)
m1
m2 g
T2
T2
m1 g
m2
5-12) Two blocks of equal mass, m1 = m2 = m , are attached to opposite ends of a light string that
is draped over a frictionless pulley. One block is constrained to move over a rough inclined plane,
as represented in the diagram below. The plane is inclined an angle θ = 37° to the horizontal and
the coefficient of kinetic friction is µk . Assume the system is released from rest. Do the
following:
a)
Draw an accurate free-body diagram and appropriate coordinate system. Use this,
and Newton’s second law, to derive a general equation for the magnitude of the
acceleration of each block.
b)
Derive a general equation for the tension.
c)
Derive an expression for the mass on the incline if the blocks had differing masses and
if, when released, they did not accelerate but moved with constant speed.
d)
Calculate the physical quantities of interest is m1 = m2 = 5 kg and µk = 0.25 .
N
ĵ
T
fk
θ
inθ
s
mg
θ
mg
î
s
co
mg
î
T
mg
a) Since we have kinetic friction, I will begin with summing forces perpendicular to the inclined
plane. We have
N − mg cosθ = may = 0 ,
(1)
so
and
N = mg cosθ ,
fk = µ k N = µ k mg cosθ .
(2)
(3)
Summing forces parallel to the incline we find
T − mg sin θ − µ k m cos θ = ma .
S 5-7
(4)
For the hanging block, we have
mg − T = ma .
We add equations (4) and (5) will eliminate the tension. When we do this, we have
mg − T + T − mg sin θ − µk mgcos θ = ma + ma = 2ma ,
a=
and
b)
c)
Using equation (5), we have
1
⎡1 − 1(sin θ + µ k cos θ )⎤⎦ g .
2⎣
T = m ( g − a) .
(5)
(6)
(7)
(8)
If m1 ≠ m2 , then equation (7) takes on the form
⎡ m1 − m2 ( sin θ + µ k cosθ ) ⎤
a=⎢
⎥g .
m
+
m
1
2
⎣
⎦
If the blocks were to move with constant velocity, then a = 0 and equation (9) implies
m1 = m2 ( sin θ + µk cosθ ) ,
(
)
and
m2 = m1 / sin θ + µ k cos θ .
d) The acceleration would be given by
a=
(
(
(10)
(11)
)
1
⎡⎣1 − 1(sin 37° + (0.25 ) cos 37°)⎤⎦ 9.81 m ⋅ s −2 = 0.97 m / s 2 .
2
The tension would be
(9)
(12)
)
T = ( 5 kg ) 9.81 m ⋅ s −2 − 0.97 m / s 2 = 44.2 N .
(13)
5-13) Two blocks, m1 and m2 , are attached to opposite ends of a light string that is draped over a
frictionless pulley. Both blocks move on rough surfaces for which the coefficient of kinetic friction
is µk . Block two moves on a surface inclined an angle θ = 53° to the horizontal, as represented
in the diagram below. A constant force of magnitude F is applied to block one causing it to
accelerate left, as viewed. Draw an accurate free-body diagram and an appropriate coordinate
system. Use the information and Newton’s second law to do the following:
a)
Derive a general equation for the magnitude of the acceleration of each block.
b)
Derive a general equation for the tension in the string.
c)
Calculate the value of the force and the tension if the magnitude of the acceleration is
1 m / s 2 and, m1 = 4 kg and m2 = 5 kg , while µk = 0.500 .
a) Summing the y forces on block one we get
N 1 − m1 g = m1 ay = 0 ,
(1)
N 1 = m1 g ,
fk1 = µk N 1 = µk m1g .
(2)
F − T − µ k m1g = m1a .
(4)
N 2 − m2 gcos θ = m2 a y = 0 ,
(5)
so
and
Summing the x forces on block one we have
(3)
Turning to block two we have
S 5-8
N 2 = m2 gcos θ ,
fk2 = µ k N 2 = µ k m2 gcos θ .
so
and
ĵ
(6)
(7)
N1
î
F
T
T
fk1
m1 g
N2
fk2
î
θ
os θ
c
g
in
gs
m2
m2
ĵ
m2 g
θ
Further,
T − m2 g sin θ − µk m2 cos θ = m2 a .
Adding equations (4) and (8) will eliminate the tension. Doing so gives us
(8)
F − T − µ k m1g + T − m2 g sinθ − µk m 2 g cosθ = m1a + m2 a .
After some algebra, we find
(
and, therefore,
b)
c)
)
F − µ k m1 + m2 ( sinθ + µk cosθ ) g = ( m1 + m 2 ) a ,
(10)
⎡ F − ( µk m1 + m2 ( sinθ + µk cosθ )) ⎤
a=⎢
⎥g.
m1 + m2
⎢⎣
⎥⎦
(11)
The tension can be found using equation (4) or (8). We have
(
)
(
)
(12)
)(
)
T = F − m1 ( µk g + a ) = m2 ( sinθ + µk cosθ ) g + a .
Using equation (10), we write
(
(9)
(
)
F = (m1 + m2 ) a + µ k m1 + m2 ( sinθ + µ k cos θ ) g
) (
= ( 4kg + 5kg) 1m / s 2 + ( 0.5 ) 4kg + 5kg (sin 53° + (0.5 ) cos 53°) 9.81 m ⋅ s −2
= 82.55 N .
(13)
The tension is
( (
) (
))
T = ( 82.55 N ) − ⎡⎣ 4kg (.5 ) 9.81 m ⋅ s −2 + 1 m / s 2 ⎤⎦ = 58.9 N .
(14)
5-14) A car of mass m travels around a circular turn of radius R at speed v , as represented in the
diagram, in a front view of the car. The road is banked for safety. For a specific speed and radius,
there is an optimal angle θ optimal at which the car can negotiate the turn safely without the need for
any friction parallel to the road surface and perpendicular to the motion. Use Newton’s second law
for circular motion to calculate the optimal banking angle.
S 5-9
N sin θ
N
N cosθ
θ
k̂
r̂
θ
R
mg
Summing the vertical forces we have
and
N cosθ − mg = mavertical = 0 ,
mg
N=
.
cosθ
(1)
(2)
Summing the radial forces we have
Therefore,
5-15)
mv 2
mg
−N sin θ = −
=−
sin θ = −mg tanθ .
R
cos θ
2
−1 ⎡ v ⎤
θ = tan ⎢ ⎥ .
⎣ Rg ⎦
N sin θ
N θ N cosθ
θ
(3)
(4)
N ′ sin θ
N′
N ′ cosθ
mg
Mg
A 70 kg pilot pilots an airplane through a horizontal, circular turn of radius 2 km , as
represented in the diagram above. The speed of the plane is 400 km / hr . The plane is subject to
four major forces. Thrust and drag which are directed out of and into the page, respectively. The
other two forces are the weight and the lift. The lift is directed perpendicular to the banking angle
θ . Do the following:
S 5-10
a)
a)
Calculate the value of the angle θ .
b)
Calculate the pilot’s apparent weight.
For the plane, the vertical forces are given by
and
Summing radial forces gives us
Therefore,
N cosθ − Mg = Mavertical = 0 ,
Mg
N=
.
cosθ
(1)
(2)
Mv 2
⎡ Mg ⎤
−N sin θ = −
= −⎢
sin θ = −Mg tan θ .
R
⎣ cos θ ⎥⎦
⎡ ( 400 (1,000 m ) / 3600 s )2
⎡ v2 ⎤
−1
θ = tan ⎢ ⎥ = tan ⎢
−2
⎣ Rg ⎦
⎢⎣ ( 2 (1,000 m )) 9.81 m ⋅ s
−1
(
)
⎤
⎥ = 32.2° .
⎥⎦
(3)
(4)
b) As to the pilot, the force exerted on the pilot by the seat is called the “apparent weight”. In
this linguistic usage, weight is associated with the value measured on an appropriate scale. So, it is
as if there is a scale between the pilot and the seat. In this case, N ′ represents the apparent weight
of the pilot. So, we have
mv 2
− N ′ sinθ = −
,
R
( 70 kg )( 400 (1,000 m ) / 3600 s )2
(5)
mv2
N′ =
=
= 811 N .
and
(6)
R sin θ
(2,000 m )( sin 32.2° )
5-16) A small block of mass m is placed inside a cylinder of radius R that rotates with a period
τ about a horizontal axis, as represented in the diagram below. A static frictional force exerted on
the block by the cylinder will carry the block through an angle ϕ m before the block begins to slip.
Do the following:
a)
Draw an accurate free-body diagram with an appropriate coordinate system. Using
Newton’s second law for circular motion, prove that
(
))
(
g sin ϕ m = µs g cos ϕ m + v 2 / R ,
where µs is the coefficient of static friction.
b)
Derive a general equation for the possible values of ϕ m in terms
ϕ m = ϕ m ( µ s , g, R,τ ) .
c)
Calculate a value for ϕ m if µs = 0.75 , R = 0.40 m , and τ = 2 s .
a) At the angle ϕ m , the static friction is at a maximum and we have
mv2
−N m + mg cos ϕ m = −
,
R
and
N m = m g cos ϕ m + (v 2 / R ) .
(
)
S 5-11
(1)
(2)
For the angle at which slipping begins, the tangential acceleration must be zero and, therefore,
(
(
fs = µ s N = mg sin ϕ m = µ s m g cos ϕ m + v2 / R
and, therefore,
(
(
g sin ϕ m = µs g cos ϕ m + v 2 / R
)) ,
)) .
(3)
(4)
ϕm
R
N
ϕ
fs
ϕ̂
mg
r̂
b)
From equation (4), we have
(
)
g sin ϕ m = µs g cosϕ m + µ s v2 / R = µ s gcos ϕ m + 4π 2 R µs / τ 2 ,
and
(
)
sin ϕ m = µs ⎡⎣ cos ϕ m + 4π 2 R / τ 2 g ⎤⎦ = µ s [cos ϕ m + C ] ,
C = 4π 2 R / τ 2 g .
where
Squaring equation (7) we get
sin2 ϕ m = µs2 ⎡⎣ cos2 ϕ m + 2C cosϕ m + C 2 ⎤⎦ .
(5)
(6)
(7)
(8)
We can rewrite equation (8) as
and
1 − cos2 ϕ m = ⎡⎣ µ 2s cos2 ϕ m + 2 µ 2s C cos ϕ m + µs2C 2 ⎤⎦ ,
µs2 cos 2 ϕ m + cos2 ϕ m + 2µ s2C cos ϕ m + µs2 C 2 − 1 = 0 .
(µ
2
s
)
+ 1 cos ϕ m + 2 µ C cosϕ m + µ C − 1 = 0 .
2
2
s
2
s
2
µs2 C
µ 2s C 2 − 1
cos ϕ m + 2 2
cos ϕ m +
=0.
µs + 1
µs2 +1
2
(9)
(10)
(11)
(12)
The roots are
2
µ s2C
⎡ µ 2s C ⎤ 1 − µs2 C 2
cos ϕ m = − 2
± ⎢− 2
⎥ + µ 2 +1 ,
µs + 1
µ
+
1
⎣ s
⎦
s
and
S 5-12
(13)
cos ϕ m = −
µs2 ( 4π 2 R / τ 2 g )
µ 2s + 1
(
⎡ µ 2s 4π 2 R / τ 2 g
± ⎢−
µs2 + 1
⎢⎣
⎡ 4π 2 Rµ 2s
4π Rµ
=− 2
± ⎢− 2
2
τ g µ 2s +1
⎢⎣ τ g µ s + 1
2
(
c)
2
s
)
(
)
2
) ⎤⎥
⎥⎦
2
+
(
1− µ s2 4π 2 R / τ 2 g
µs2 + 1
(
⎤ 1− 4 π 2 R µs / τ 2 g
⎥ +
µ 2s + 1
⎥⎦
)
)
2
2
.
(14)
Using the values given we have
cos ϕ m = −0.1449 ±
(−0.1449)2 + 0.5817 = 0.6314
,
(15)
and, therefore,
ϕ m = cos−1 ( 0.6314 ) = 50.8° .
(16)
5-17) A daredevil cyclist of mass m moves with speed v in a horizontal circle of radius R in a
cylindrical “well of death,” as represented in the diagram below. Do the following:
a)
Draw an accurate free-body diagram with an appropriate coordinate system. Use
Newton’s second law to derive a general equation for the minimum coefficient of
static friction required for the stunt to be successful.
b)
Calculate the value of the minimum coefficient of static friction if v = 7 m / s and
R = 4 m .
R
m
k̂
r̂
N
mg
fs
a) For the minimum value of the static friction, the static friction would be a maximum and
summing vertical forces would give us
µs N − mg = mavertical = 0 .
(1)
µs =
Therefore,
Summing radial forces we find
mg
.
N
mv 2
−N = −
.
R
(2)
(3)
Substitution of equation (3) into (2) yields
µs =
mg
Rg
= 2 .
2
mv / R v
S 5-13
(4)
b)
For the values given, we have
( 4 m ) (9.81 m ⋅ s −2 )
µs =
= 0.80 .
( 7 m / s )2
(5)
5-18) An atwood machine was a machine that facilitated experimental confirmation of Newton’s
second law. It was, and still is, used to measure g . Two block of equal mass M hang on either
side of a pulley. A small square “rider” of mass m is placed on one of the blocks, as represented
in the diagram below. When released from rest the system accelerates for a distance h until the
rider is “caught” by a ring that allows the block to pass through. The block then moves a distance
 at a constant speed for some time t . Show that the experimental value of g is given by
g = (2M + m ) 2 / 2mht 2 .
m
M
h
M
to = 0
T
T

t
Mg
( M + m) g
A free-body diagram of the accelerating masses may prove useful. (See above.)
For the block without the rider, we have
T − Mg = Ma ,
while for the block and rider we have
( M + m) g − T = ( M + m) a .
Adding equations (1) and (2) eliminates the tension and gives us
( M + m ) g − T + T − Mg = ( M + m ) a + Ma ,
and
a = mg / (2 M + m ) .
(1)
(2)
(3)
(4)
As the acceleration is constant and the initial speed is zero, the speed of the rider at the instant
it is “caught” is given by
v = 2ah = 2mgh / (2M + m ) .
(5)
The speed of the riderless mass at the instant it has moved the distance  in time t is given
by equation (5)--the acceleration is constant over this time interval. So,
v = 2mgh / 2M + m =  / t .
Squaring equation (6) and solving for g we have
2mgh / (2M + m ) = 2 / t 2 → g = (2M + m )  2 / 2mht 2 .
S 5-14
(6)
(7)
5-19) The electron in a hydrogen atom orbits a stationary proton with a speed 2.2 ×10 m / s .
−11
We model the orbit as circular, centered on the proton, with radius R = 5.3 × 10 m . Do the
following:
a)
Calculate τ , the period of the electron in its orbit of the proton.
b)
Calculate the magnitude of the net force acting on the electron.
6

v
R

FE
−e
e
a)
ϕ̂
me
r̂
The path is circular and the speed is constant, so we have
2π R
,
τ
2π 5.3 × 10−11 m
v=
τ=
and
b)
(
(1)
)
)
2π R
=
= 1.51 × 10−16 s .
6
v
2.2 ×10 m / s
(
The magnitude of the electrical force is given by
v2
−F = −me
,
R
E
and
(2)
(
F = 9.109 × 10
E
( 2.2 × 10 m / s)
kg )
(5.3 ×10 m )
6
−31
−11
(3)
2
= 8.32 ×10 −8 N .
(4)
5-20) A small block of mass m moves with constant speed v on a horizontal circular path, as
represented in the diagram above. The radial (centripetal) force exerted on the small mass is
provided by a light string attached to a hanging mass M . The coefficient of static friction is µs .
Show that the ratio of Rmax to Rmin , the maximum and minimum possible radii, respectively, is
given by
Rmax M + µ s m
=
.
Rmin M − µ s m
In general, summing vertical forces on the hanging mass, we find
T − Mg = Mavertical = 0 → T = Mg .
(1)
The net radial force on the moving mass depends on the static friction orientation. The minimum
radius occurs when the tension and static friction are both directed toward the center. The
maximum radius occurs when the tension and static friction are directed oppositely. So, for
minimum radius, we have
−T − µs N = −Mg − µ s mg = −mv 2 / Rmin ,
(2)
and
Rmin ( M + µ s m ) g = mv2 .
S 5-15
(3)
N

v
R
T
fs
N
fs
T fs
Rmin
mg
Rmax
T

vmax
mg
Mg
The maximum radius occurs when the direction of the radial forces are opposite. So, we have
−T + µs N = −Mg + µ s mg = −mv 2 / Rmax ,
(4)
and
Therefore,
Rmax ( M − µs m ) g = mv 2 = Rmin ( M + µ s m ) g .
Rmax M + µ s m
=
.
Rmin M − µ s m
(5)
(6)
5-21)
θ
8

5

k̂
TU
m
R
r̂
mg
θ
TL

A block of mass m is attached to a vertical rotating spindle by two light strings of equal length  ,
as represented in the diagram above. The period of the spindle’s rotation is τ . Using Newton’s
second law, do the following:
a)
Derive a general equation for TU , the tension in the upper string.
Derive a general equation for TL , the tension in the lower string. (The tensions are
not the same. Your equations should have a functional form
T = T ( m, ,g,τ ) . )
Summing the vertical forces on the block, we have
b)
a)
S 5-16
TU cos θ − TL cos θ − mg = mavertical = 0 ,
mg
5
TU − TL =
= mg .
cosθ 4
and
(1)
(2)
Summing the radially directed force we get
⎛ 2π ⎞
−TU sin θ − TL sinθ = −mRω = −m (  sin θ )⎜
,
⎝ τ ⎟⎠
2
2
and
TU + TL = 4π m / τ .
Adding equations (2) and (4) eliminates the lower tension leaving us
2
2
(4)
5
2
2
mg + 4π m / τ ,
4
m ⎡ 4π 2 5 ⎤
TU = ⎢ 2 + g ⎥ .
2⎣ τ
4 ⎦
TU − TL + TU + TL =
and
b)
(3)
(5)
(6)
Substitution of equation (6) into equation (2) yields
m ⎡ 4π 2  5 ⎤ 5
m ⎡ 4π 2  5 ⎤ 5 m
m ⎡ 4π 2  5 ⎤
TL = ⎢ 2 + g ⎥ − mg = ⎢ 2 + g ⎥ −
g = ⎢ 2 − g⎥ .
2⎣ τ
4 ⎦ 4
2⎣ τ
4 ⎦ 2 2
2⎣ τ
4 ⎦
24
5-22) Model the Earth as a uniform sphere of mass M ⊕ = 5.97 × 10 kg and radius
(7)
R⊕ = 6.371 × 10 6 m . At the surface, g = go = 9.810 m / s 2 . At a height h above the
surface, g < go . The ratio g / go can be used to measure h . Use the model and Newton’s law of
universal gravitation to derive a general equation for h in terms of g / go and R⊕ .
R⊕
P
h
M⊕
We can write
g=
GM ⊕
=
GM⊕
( R⊕ + h )2 ( R⊕ (1 + h / R⊕ ))2
=
Rearranging terms, we have
while
1 + h / R⊕ =
⎡ GM ⎤
1
= ⎢ 2⊕ ⎥
2
⎣ R⊕ ⎦ (1+ h / R⊕ )
go
.
(1 + h / R⊕ )2
g
(1 + h / R⊕ )2 = o
g
(1)
,
⎡ g
⎤
go
→ h = R⊕ ⎢ o − 1⎥ ,
g
⎣ g
⎦
S 5-17
(2)
(3)
5-23)
ϕ

m
A simple pendulum is represented in the diagram above. The period τ of a simple pendulum
of length  , bob mass m and for which ϕ , the angular displacement, is small, is given by
τ = 2π  / g .
2
It is adjusted to keep correct time at sea level where g = 9.810 m / s . When this “clock” is
moved to the top of a mountain, it loses 1 min / day . Do the following:
a)
Calculate the value for g at the top of the mountain.
a)
b)
Calculate the height of the mountain.
At sea level, then,
τ = 2π  / g .
(1)
The value for the period on the mountain top is given by
τ top = (τ + t ) = 2π  / gtop ,
(2)
where t is the “loss”. The square of the ratio of equations (1) and (2) gives us
τ2
and
b)
gtop
gtop
4π 2  / g
=
=
,
2
4 π  / gtop
g
(τ + t )2
2
24 (60 ))
τ2
(
−2
−2
=
2 g =
2 ( 9.810 m ⋅ s ) = 9.796 m ⋅ s .
(τ + t )
( 24 ( 60 ) +1)
(4)
Using what we found in the preceding problem, we can write
⎡ g
⎤
⎡ 9.810
⎤
6
h = R⊕ ⎢ o −1⎥ = 6.371 × 10 m ⎢
− 1⎥ = 4.55 km .
⎣ g
⎦
⎣ 9.796
⎦
(
5-24)
(3)
R⊕
)
m
MM
M⊕
M
r⊕M
r⊕
A person of mass m = 70 kg stands on the surface of the Earth; the Earth modeled in
problem 5-22). Do the following:
S 5-18
(5)
a)
G
m⊕
F
b)
Calculate the magnitude of the gravitational force exerted on the person by the Earth.
(
(
)
(
)
Calculate the magnitude of the gravitational force exerted on the person by the Moon.
22
8
(The mass of the Moon is M M = 7.36 × 10 kg and r⊕M = 3.84 × 10 m is the
average distance from the center of the Earth to the center of the Moon.)
G
mM
F
c)
)
6.67 ×10 −11 N ⋅ m2 ⋅ kg −2 ( 70 kg ) 5.97 ×10 24 kg
GmM ⊕
=
=
= 687 N .(1)
2
R⊕2
6.371 × 106 m
(
)
(
)
6.67 × 10−11 N ⋅ m 2 ⋅ kg −2 ( 70 kg ) 7.36 × 1022 kg
GmM M
=
=
2
2
r⊕M
3.84 ×10 8 m
(
)
= 0.0023 N .
(2)
Calculate the magnitude of the gravitational force exerted on the person by the Sun.
30
11
(The mass of the Sun is M  = 1.99 × 10 kg and r⊕ = 1.496 × 10 m is the
average distance from the Earth to the Sun.)
G
mM
F
(
)
(
6.67 × 10−11 N ⋅ m 2 ⋅ kg −2 ( 70 kg ) 1.99 ×10 30 kg
GmM M
=
=
2
2
r⊕M
1.496 × 1011 m
(
)
= 0.415 N .
5-25) Using the data of the preceding problem, do the following:
a)
Calculate the magnitude of the Moon’s gravitational field at the Earth.
b)
Calculate the magnitude of the Sun’s gravitational field at the Earth.
a) The magnitude of the Moon’s gravitation field at the Earth is given by
(
)(
)
)
(3)
)
6.67 × 10 −11 N ⋅ m 2 ⋅ kg−2 7.36 ×10 22 kg
GM M
−5 m
gM =
=
=
3.3
×10
2
2 . (1)
8
rM ⊕
s
3.84 ×10 m
b)
(
The magnitude of the Sun’s gravitational field at the Earth
(
)(
)
6.67 × 10 −11 N ⋅ m 2 ⋅ kg−2 1.99 × 10 30 kg
GM M
−3 m
g =
=
=
5.9
×10
. (2)
2
rM ⊕
s2
1.496 × 1011 m
(
)
5-26) The gravitational field at any point outside a uniform spherical mass distribution can be
calculated as if all of the mass were at the center of the sphere. (Spheres have point symmetry.)
Represented in the diagram below is a uniform sphere of mass M and radius R from which a
spherical segment radius R / 2 has been removed. Calculate the magnitude of the net gravitational
force that would be exerted on a test mass mt at a point a distance  from the center of the original
sphere, where  > R . The test mass is on a radial line that passes through the center of the hole.
The “mass” of the hole is proportional to the ratios of the volumes of the hole to the original
sphere.
M hole
⎡ ( 4 / 3) π ( R / 2 ) 3 ⎤
M
= −⎢
M
=
−
.
⎥
3
8
⎢⎣ ( 4 / 3)π R
⎥⎦
So, the gravitational field at the point of the test mass is given by
S 5-19
(1)
⎡1
⎤
⎤
GM ⎡
M /8
1
/
8
⎥
⎥ = −GM ⎢ 2 −
g=− 2 +⎢
2
2

⎢

⎢⎣ ( − ( R / 2 )) ⎥⎦
 (1 − ( R / 2)) ⎥⎦
⎣
⎡
⎤
⎢
⎥
⎤
GM
1/8
GM ⎡
4 2 / 8 ⎤
GM ⎡
2
⎢
⎥
= − 2 1−
=
−
1
−
=
−
1
−
⎢
⎥
⎢
⎥ . (2)
 ⎢ ⎛ 2 − R ⎞ 2 ⎥
2 ⎢⎣ ( 2 − R )2 ⎥⎦
2 ⎢⎣ 2 ( 2 − R )2 ⎥⎦
⎢ ⎜⎝
⎟ ⎥
2 ⎠ ⎦
⎣
(
)
M
mt
R
0.5 R

Therefore, the magnitude of the gravitational force is given by
G
⎤
GMmi ⎡
2
Fmi M = mi g =
1−
⎢
⎥.
2 ⎢⎣ 2 (2 − R )2 ⎥⎦
(3)
5-27) For small angular displacements, the period of a simple pendulum of length  and “bob”
mass m is given by
τ ⊕ = 2π  / g ,
2
where, at the surface of the Earth, g⊕ = 9.810 m / s . Do the following:
a)
Calculate the value of  if at the Earth’s surface the period is 2 s .
b)
a)
Calculate the value of the period of this “clock” if it were transported to the surface of
the Moon. Recall, M ⊕ ≈ 81.1 M M and R⊕ ≈ 3.7 RM .
The length of the pendulum is given by
τ ⊕2 = 4 π 2  / g ,
(1)
−2
τ ⊕2 g (2 s ) ( 9.81 m ⋅ s )
=
=
= 0.994 m ≡ 99.4 cm .
4π 2
4π 2
2
and
The period of this “clock” on the Moon would be given by
τ M2 = 4π 2  / gM .
The ratio of equations (3) and (1) gives
(2)
b)
S 5-20
(3)
τ M2
4π 2  / g M
=
→ τ M =
τ ⊕2
4π 2  / g
g
τ ⊕ .
gM
(4)
We know also that
2
g
GM ⊕ / R⊕2 ⎛ M ⊕ ⎞ ⎡ RM ⎤
2
(
)
(
)
=
=
81.1
1
/
3.7
= 5.924 .
⎢
⎥
2 = ⎜
gM GM M / RM ⎝ M M ⎟⎠ ⎣ R⊕ ⎦
Equations (5) and (4) imply
(5)
τ M = 5.924 ( 2 s ) = 4.87 s .
(6)
5-28)
M
G
m
Fmn
R
FmfG m
2
1
a
a
r
A dumbbell consisting of two point masses of equal mass m separated by a massless rod of
length 2a oriented along a radial line of a uniform spherical mass M is represented in the
diagram above. Assume that M >> m and the gravitational interaction between the two point
masses is negligible. Do the following:
a)
Calculate the magnitude of the net gravitational force exerted each point mass due to its
mass interaction with the sphere.
b)
Calculate the difference between these two magnitudes. (This difference would result
in a tension in the rod. This tensile force is an example of a “tidal” force.)
c)
Show that if r >> a , then
ΔF =
a)
4GMma
.
r3
The gravitational force on the nearest point mass is given by
Fm1 =
G
GMm
(r − a )2
.
(1)
The gravitational force on the point mass farthest is given by
Fm2 =
G
b)
GMm
( r + a )2
.
(2)
The difference is given by
ΔF =
G
GMm
−
GMm
( r − a )2 (r + a )2
⎡
⎤
1
1
⎥,
= GMm ⎢
−
2
2
⎢⎣ r 2 (1 − ( a / r ))
r 2 (1+ ( a / r )) ⎥⎦
S 5-21
(3)
and
GMm ⎡ ⎛
a⎞
ΔF = 2 ⎢ ⎜ 1− ⎟
r ⎣⎝
r⎠
G
c) We know that for t << 1 , (1 + t ) ≈ 1 + nt .
Using this, we can write
−2
−2
a⎞ ⎤
⎛
− ⎜1 + ⎟ ⎥ .
⎝
r⎠ ⎦
n
a⎞
⎛
⎜⎝ 1 − r ⎟⎠
−2
while
⎛
⎜⎝ 1 +
a⎞
r ⎟⎠
(4)
(5)
≈ 1 + ( −2)( −a / r ) = 1 + 2a / r ,
(6)
≈ 1 + ( 2) (−a / r ) = 1 − 2a / r .
(7)
−2
Substitutions of these approximations into equation (4) gives us
ΔF ≈
G
5-29) GMm
4GMma
⎡ (1 + 2a / r ) − (1− 2a / r )−2 ⎤ =
.
2
⎦
r ⎣
r3
î
î
T
m1 g
T
m2 g
cosθ
m2 g
(8)
N
θ m2 g
sin θ
Two blocks of mass m1 and m2 , where m1 > m2 , are connected to opposite ends of light
string. In turn, the string is draped over a frictionless pulley. Block two is constrained to move over
a smooth inclined plane, as represented in the diagram above. The plane is inclined an angle θ to
the horizontal. Assuming the system is released from rest and mass one moves downward, do the
following:
a)
Using Newton’s second law, derive an equation of the magnitude of the acceleration of
each block relative to the Earth.
b)
Derive an equation for the tension in the string.
c)
Derive an equation for the speed of each block at the instant each block has moved a
distance  .
d)
If m1 = 12 kg , m2 = 8 kg , θ = 20° and  = 0.75 m , calculate the values of the
quantities of interest in parts a) b) and c).
a) We begin with a free-body diagram. Summing the forces on the block moving downward, we
have
m1 g − T = m1a .
(1)
Summing the forces on the block moving parallel to the inclined plane we find
T − m2 g sin θ = m2 a .
(2)
adding equations (1) and (2) yields
S 5-22
m1 g − T + T − m2 g sin θ = m1 a + m2 a ,
(m1 − m2 sin θ ) g = ( m1 + m2 ) a .
and
Therefore,
b)
(3)
(4)
⎡ m − m2 sin θ ⎤
a=⎢ 1
⎥g.
⎣ m1 + m2 ⎦
(5)
Using equation (1), we can write
⎛
m − m2 sin θ ⎞
T = m1 ( g − a ) = m1 ⎜ g − 1
g⎟
m1 + m2
⎝
⎠
⎛ m1 + m2 − ( m1 − m 2 sin θ ) ⎞
m1 m2 g
= m1 ⎜
g
=
1
+
sin
θ
(
)
.
⎟
m1 + m2
m1 + m2
⎝
⎠
c)
As the acceleration is constant and the initial speed is zero, we have
⎡ m − m2 sin θ ⎤
v = 2a = ⎢ 1
⎥ 2g .
m
+
m
⎣
1
2
⎦
d)
(6)
(7)
For the acceleration, we have
⎡ (12kg ) − (8kg ) sin 20° ⎤
⎡ m − m2 sin θ ⎤
a=⎢ 1
g
=
9.81 m ⋅ s −2
⎥
⎢
⎥
⎣ m1 + m2 ⎦
⎣ (12kg) + (8kg)
⎦
2
= 4.54 m / s .
(
The tension in the string is given by
(1 + sin 20°)(12 kg ) (8 kg )( 9.81 m ⋅ s −2 )
T=
= 63.2 N .
(12 kg ) + (8 kg)
)
(8)
(9)
The speed is given by
⎡ (12kg ) − (8kg) sin 20° ⎤
m
v = ⎢
2 9.81 m ⋅ s −2 ( 0.75 m ) = 2.61 2 .
(10)
⎥
12kg
+
8kg
s
(
)
(
)
⎣
⎦
5-30) Re-do the preceding problem this time with friction on the incline. Use µk for the
coefficient of kinetic friction. For part d), let µk = 0.35 . The free-body diagram is shown below.
(
)
Summing forces again we find this time
m1 g − T = m1a ,
T − m2 g sin θ − µk m2 g cos θ = m2 a .
(1)
m1 g − T + T − m2 g sin θ − µk m2 g cosθ = m1a + m 2 a ,
(3)
⎡ m1 − m2 ( sin θ + µ k cosθ ) ⎤
a=⎢
⎥g .
m
+
m
1
2
⎣
⎦
(4)
and
Adding these two equations gives us
and, therefore,
S 5-23
(2)
î
î
T
T
fk
m2 g
cosθ
m2 g
m1 g
N
θ m2 g
sin θ
The tension is given by
⎛
m1 − m2 ( sinθ + µk cosθ ) ⎞
T = m1 ( g − a ) = m1 ⎜ g −
g⎟
m1 + m2
⎝
⎠
⎛ m1 + m2 − ( m1 − m 2 (sin θ + µ k cos θ ))⎞
m1 m2 g
= m1 ⎜
.(5)
⎟ g = (1+ sin θ + µ k cos θ )
m1 + m2
m1 + m2
⎝
⎠
The speed, then, is given by
⎡ m1 − m2 ( sin θ + µk cosθ ) ⎤
v = 2a = ⎢
⎥ 2g .
m
+
m
1
2
⎣
⎦
(6)
Using the values given, the acceleration is given by
⎡ (12kg) − (8kg ) (sin 20° + .35 cos 20°) ⎤
m
−2
a=⎢
9.81 m
⋅
s
=
3.25 .
⎥
s2
(12kg ) + ( 8kg )
⎣
⎦
(7)
(1 + sin 20° + .35 cos 20°)(12 kg) (8 kg ) (9.81 m ⋅ s −2 )
T=
= 78.7 N .
(12 kg ) + ( 8 kg )
(8)
(
)
The tension is
The speed is
⎡ (12 kg ) − ( 8 kg )( sin 20° + .35 cos 20°) ⎤
v = ⎢
2 9.81 m ⋅ s −2 (0.75 m)
⎥
(12 kg ) + (8 kg)
⎣
⎦
= 2.21 m / s .
(9)
5-31) A block of mass m is released from rest at the top of a smooth inclined plane that makes an
angle θ , with respect to the vertical, as represented in the diagram above. The release point is a
vertical distance h above a level, rough surface for which the coefficient of kinetic friction is µk .
(
)
Do the following:
a)
Derive an equation for the speed of the block at the bottom of the incline.
b)
Assuming an uneventful transition at the bottom, derive an equation for the distance 
the block will slide along the level, rough surface for coming to rest.
c)
If m = 5 kg , h = 2 m , θ = 25° and µk = 0.42 , find the values of the physical
quantities of interest in parts a) and b).
S 5-24
a)
Summing the forces parallel to the frictionless incline we get
mg cos θ = ma ,
and, therefore,
a = g cos θ .
As the acceleration is constant and the initial speed zero, we can write
(1)
(2)

v = 2a ( Δ r ) = 2 (g cos θ )(h / cosθ ) = 2gh .
b)
Summing vertical forces over the rough surface, we have
N ′ − mg = may = 0 ,
(4)
N ′ = mg ,
fk = µ k mg .
so
and
(3)
(5)
(6)
N
h
θ
N′
mg
si
fk
nθ
mg
θ
mg
cos
θ
mg
Summing forces parallel to the motion we find
− µk mg = ma ,
a = − µk g .
(7)
and
As the acceleration over the rough surface is constant, we can write
v 2 = 0 = vo2 + 2 − µk g  ,
(
and
c)
)
vo2
2gh
h
=
=
=
.
2 µk g 2 µ k g µ k
(8)
(9)
(10)
For the values given, the speed at the bottom of the hill would be
(
)
v = 2gh = 2 9.81 m ⋅ s −2 (2 m ) = 6.26 m / s .
(11)
The distance the block would slide on the level surface is given by
=
h
2 m
=
= 4.76 m .
µ k 0.42
(12)
5-32) A small sphere of mass m is attached to one end of a light string of length  . The other end
of the string is attached to a horizontal rod of length a . The horizontal rod is attached to a vertical
spindle that rotates at a constant angular speed with a period τ , as represented in the diagram
below. When rotating at this angular speed, the string makes an angle θ to the vertical. Do the
following:
a)
Derive an equation for the radius of the horizontal circular path on which the sphere will
move.
b)
Derive an equation for the tension in the string.
S 5-25
c)
d)
Derive an equation for the speed of the sphere.
If m = 2 kg , = 2a = 1 m , θ = 63.44° and τ = 1.675 s , calculate the values for
the physical quantities of interest in parts a), b) and c).
a

θ
T cos θ
k̂
T
m
T sin θ
R = a +  sinθ
r̂
mg
τ
a)
The radius is given by
b)
Summing the vertical forces we find
and
c)
R = a +  sinθ .
(1)
T cos θ − mg = mavert = 0 ,
mg
T=
.
cosθ
(2)
(3)
Summing radial forces, we have
mv2
mg sin θ
−T sin θ = −
=−
= −mg tanθ .
R
cosθ
So, the speed is given by
v = Rg tan θ =
d)
(a +  sinθ ) gtan θ
.
(4)
(5)
For the values given, we have, for the radius,
R = a +  sinθ = (0.5 m ) + (1 m ) sin 63.44° = 1.394 m .
The tension is given by
T=
( 2 kg )( 9.81 m ⋅ s −2 )
The speed of the bob is given by
v=
cos63.44°
= 43.9 N .
((0.5 m ) + (1 m ) sin 63.44° )( 9.81 m ⋅ s ) tan 63.44° = 5.23 m / s .
−2
(6)
(7)
(8)
A block of mass m is released from rest a distance ho above an elastic spring with
5-33)
spring constant ksp . Do the following:
a)
b)
Use Newton’s second law to derive a general equation for vo , the speed of the block at
the instant it strikes the spring.
Draw a free-body diagram of the relevant forces acting on the block after it strikes the
spring but before it comes to instantaneous rest. Use this free-body diagram to derive
S 5-26
a general equation for the acceleration of the block relative to the floor to which the
spring is secured. (Assume the x-axis is parallel to the motion of the block.)
c)
dv dv dx
=
to generate a differential equation. Solve the differential
dt dx dt
equation to find xmax , the maximum compression of the spring.
Use a =
−1
If m = 10 kg , ho = 2 m and ksp = 5,123 N ⋅ m , then find the values of the
physical quantities of interest in parts a) and c).
The acceleration of gravity over the short fall is constant, so we can write
d)
a)
v 2 = 0 + 2gho → v = 2gho .
(1)
b)
m
ho
x=0
ksp x
x
ksp
mg
î
c)
The forces acting on the block are given by
mg − k sp x = ma ,
(2)
and
a=−
So,
k sp
m
dv v = −
Integrating, we find
0
∫
dv v = −
2 gho
1 2
v
2
0
=−
2 gho
k sp
2m
x+g =
ksp
m
k sp
m
dv v
.
dx
(3)
x dx + g dx .
x max
∫
0
(4)
x max
x dx + g
∫
dx
0
x max
x
x max
+ gx 0
2
= −gho = −
0
ksp
2m
xmax + gx max .
2
(5)
So,
−
We can rearrange equation (6) into
ksp
2m
xmax + gx max + gho = 0 .
2
S 5-27
(6)
⎡ mg ⎤
⎡ mg ⎤
2
xmax
− 2⎢
x
−
2
⎥ max
⎢ ⎥ ho = 0 .
k
⎢⎣ sp ⎥⎦
⎢⎣ k sp ⎦⎥
(7)
The roots of this equation are
2
xmax
⎡ mg ⎤
⎡ mg ⎤
⎡ mg ⎤
=⎢
±
+
2h
⎥
⎢
⎥
⎥ ,
o ⎢
k
k
k
⎢⎣ sp ⎥⎦
⎢⎣ sp ⎦⎥
⎢⎣ sp ⎥⎦
(8)
of which the negative is not physically meaningful.
5-34)
N
T
fk
m2 g
T
T
2T
2T
m1 g
Carefully consider the diagram above. Mass m2 is constrained to move over a level, rough
surface. When m1 = 3 kg then a1 = 0.60 m / s . However, a1 = 1.60 m / s if
2
2
m1 = 4 kg . Do the following:
a)
Calculate the value of m2 .
b) Calculate the magnitude of the frictional force on m2 .
(Note that the blocks do not have the same magnitude of acceleration. Treat the pulleys as massless
and frictionless.)
For the first state, we have for block one
m1 g − 2T = m1 a ,
(1)
and
For the other block
and
m1
( g − a) .
2
T − fk = m2 (2a ) = 2m2 a ,
T=
m1
(g − a ) − fk = m 2 (2a) = 2m2 a .
2
S 5-28
(2)
(3)
(4)
Therefore,
2 fk = m1 ( g − a ) − 4m2 a .
(5)
For the second state, we would have
and
Rearranging terms,
2 fk = m1′ ( g − a ′ ) − 4m2 a ′ ,
(6)
m1′ ( g − a′ ) − 4m2 a ′ = m1 ( g − a ) − 4m 2 a .
(7)
m1′ ( g − a′ ) − m1 (g − a ) = 4m2 ( a′ − a ) ,
(8)
and, therefore,
m2 =
b)
m1′ ( g − a′ ) − m1 ( g − a ) ( 4 )( 9.81 − 1.6 ) − ( 3)( 9.81 − 0.6 )
=
kg = 1.30 kg . (9)
4 (a ′ − a )
4 (1.6 − 0.6 )
Using equation (5), we have
1
1
⎡⎣ m1 ( g − a ) − 4m2 a ⎤⎦ = ⎡⎣ ( 3) (9.81 − 0.6 ) − 4 (1.3)( 0.6 )⎤⎦ N
2
2
= 12.26 N .
(10)
5-35) Two blocks of equal mass m1 = m2 = m are attached to opposite ends of a light string that
fk =
is draped over a frictionless pulley, as represented in the diagram below. Block two is constrained
to move over a rough inclined plane. The plane is inclined an angle θ to the horizontal. The
coefficient of kinetic friction between the block and the surface is µk . Assume the system is
released from rest. Do the following:
a)
Use Newton’s second law to derive an equation for the magnitude of the acceleration of
the acceleration of each block.
b)
If m1 = m2 = 5 kg , θ = 37° and µk = 0.25 , calculate the value of the magnitude
of the acceleration of each block .
c)
Calculate the speed of each block at the instant each block has moved a distance
 = 1.25 m .
T
N
fk
î
mg
a)
θ
T
mg cos θ
mg sinθ
î
mg
For the block on the incline, summing forces perpendicular to the incline we have
N − mg cosθ = ma⊥ = 0 ,
and
N = mg cosθ ,
and the kinetic friction
fk = µ k N = µ k mg cosθ .
Summing the forces parallel to the incline we have
T − mg sin θ − µ k mg cosθ = ma .
For block one, we have
S 5-29
(1)
(2)
(3)
(4)
mg − T = ma .
(5)
T − mg sin θ − µ k mg cosθ + mg − T = 2ma ,
(6)
Adding equations (4) and (5) yields
and
mg ⎡⎣1 − ( sin θ + µ k cos θ )⎤⎦ = 2ma ,
1
a = ⎡⎣1 − ( sin θ + µk cosθ )⎤⎦ g .
2
and
b)
(7)
(8)
The value of the acceleration
a=
(
)
1
⎡⎣1 − ( sin 37° + ( 0.25 ) cos 37°)⎤⎦ 9.81 m ⋅ s −2 = 0.97 m / s 2 .
2
(9)
c) As the acceleration is constant and the initial speed is zero, we have, for the speed after having
moved a distance 
(
)
v = 2a = 2 0.97 m / s 2 (1.25 m) = 1.56 m / s .
(10)
5-36) A block of mass mb is on the front of a cart of mass mc , as represented in the diagram

above. A force F acts on the cart parallel to the smooth level floor over which the system moves.
Do the following:
a)
Draw an accurate free-body diagram of the forces acting on the cart. Use Newton’s
second law to derive a general equation for the acceleration of the cart.
b)
Draw an accurate free-body diagram of the forces acting on the block. Use Newton’s
second law to derive a general equation for the acceleration of the block.
c)
Derive an equation for µs ,min , the minimum coefficient of static friction required to
keep the block from sliding off.
d)
If mb = 2 kg , mc = 3 kg and F = 60 N , calculate the value of µs ,min .
N
fs

F
N′
N′
ĵ
fs
mc g
a)
and
mb g
î
Summing the vertical forces on the cart we have
N − mc g − fs = mcavert = 0 ,
N = mc g + fs .
(1)
(2)
Summing the horizontal forces on the cart we find
F − N ′ = mc a ,
and
S 5-30
(3)
a=
b)
F − N′
,
mc
(4)
Summing the vertical forces on the block we get
fs − mb g = mb avert = 0 .
fs = mb g ,
(5)
Therefore,
and, substituting equation (6) into equation (2) yields
(6)
N = mc g + mb g = ( mc + mb ) g .
(7)
Summing the horizontal forces on the block we find
c)
N ′ = mb a .
Substitution of equation (8) into equation (3) leaves
(8)
F − mb a = mca ,
F = (mb + mc ) a ,
F
a=
.
mb + mc
and
and
(9)
(10)
(11)
Substituting equation (11) into equation (8) leaves
⎡ F ⎤
N ′ = mb ⎢
⎥ .
m
+
m
⎣ b
c ⎦
(12)
⎡ ⎡ F ⎤⎤
fs = µ s N ′ = µ s ⎢ mb ⎢
⎥ ⎥ = mb g .
m
+
m
c ⎦⎦
⎣ ⎣ b
(13)
If we calculate for the minimal value for the coefficient of static friction, then at that value
motion would be impending and we could write
Therefore,
µs = ( mb + m c )
d)
For the values given by
g
.
F
(14)
⎡ 9.81 ⎤
µs = ( 2 + 3) ⎢
⎥ = 0.82 .
⎣ 60 ⎦
(15)
5-37) A block of mass m is placed on a second block the mass of which is M , as represented in
the diagram below. The two masses are connected by a light string. The pulley is frictionless. Do
the following:
a)
Draw an accurate free-body diagram of the relevant forces acting on each block. Use
Newton’s second law to derive a general
equation for the magnitude of the acceleration

of each block if a constant force F is applied to block M in the direction indicated.
The coefficient of kinetic friction for all level surfaces is µk .
b)
If m = 2 kg , M = 4 kg and µk = 0.20 , calculate the magnitude of the applied
2
force that would accelerate each block with a magnitude 2 m / s .
S 5-31
N′
T
fk1
mg
N
mg
ĵ
î
T
Mg
a)
fk1

F
fk2
Summing the vertical forces on the top block,
N ′ − mg = mavert = 0 ,
N ′ = mg ,
fk1 = µk mg .
and
and
(1)
(2)
(3)
Summing the horizontal forces on the top block gives us
T − µ k mg = ma .
Summing the vertical forces on the bottom block results in
(4)
N − mg − Mg = Mavert = 0 ,
N − = (m + M )g ,
fk2 = µ k ( m + M ) g .
and
and
(5)
(6)
(7)
Summing the horizontal forces on the bottom block gives us
and
and, therefore,
b)
F − µk mg − µ k mg − ma − µk ( m + M ) g = Ma .
F − µk [3m + M ] g = ( m + M ) a ,
F − µ k [ 3m + M ] g
a=
.
(m + M )
(8)
(9)
(10)
For the values given, we have
F = (m + M ) a + µ k [ 3m + M ] g
(
)
= ⎡⎣( 2 + 4 )( 2) + (.2 )( 3( 2 ) + 4 ) 9.81 m ⋅ s −2 ⎤⎦ N = 31.62 N .
(11)
5-38) A so-called conical pendulum is represented in the diagram below. A “bob” of mass m is
attached to one end of a light string of length  . The other end is attached to a frictionless pivot.
The bob is given a horizontal push that results in horizontal circular motion in which the angle the
string makes to the vertical remains at a constant value θ . Use Newton’s second law of motion to
S 5-32
show that τ , the period of this motion, is given by
τ = 2π cos θ / g .
θ

T cos θ
T
R =  sin θ
T sin θ
m

vtangential
k̂
ϕ̂
mg
r̂
Summing the vertical forces,
mg − T cosθ = mavert = 0 ,
(1)
and
T=
Summing the radial forces we find
mg
.
cosθ
(2)
mv 2
m ( 2π  sin θ / τ )
⎡ mg ⎤
−T sin θ = − ⎢
sin
θ
=
−mg
tan
θ
=
−
=
−
,
 sin θ
 sinθ
⎣ cosθ ⎥⎦
2
and
Therefore,
4π 2 m sinθ
mg tan θ =
.
τ2
(3)
(4)
4 π 2 m sin θ
 cosθ
τ=
= 2π
.
(5)
mgtan θ
g
5-39) A car travels in a horizontal circle of radius r on a road banked at an angle θ to the
horizontal, as represented in the diagram above. The coefficient of static friction is µs . Do the
following:
a)
Show that the maximum speed possible without breaking free and sliding up the incline
is given by
vmax =
rg ( µ s + tanθ )
.
1 − µ s tan θ
b)
Calculate the minimum speed possible without sliding down the incline.
a) At maximum speed, the car is in danger of sliding “up” the incline and motion is
impending. So, summing the vertical forces gives us
S 5-33
N cosθ − µ s N sin θ − mg = mavert = 0 ,
N ( cosθ − µ s sin θ ) = mg .
and
θ
Max Speed
N
fs
(1)
(2)
k̂
N
s
=µ
θ
r̂
r
mg
Summing radial forces we have
mv2max
N ( sin θ + µs cos θ ) =
.
r
(3)
Dividing equation (2) by equation (3) results in
N ( cosθ − µ s sin θ )
N ( sin θ + µs cos θ )
and
vmax =
=
mg
rg cos θ − µ s sinθ
= 2 =
,
2
mvmax / r v max sin θ + µs cosθ
(4)
rg ( sin θ + µ s cos θ ) 1 / cos θ
( cosθ − µ s sin θ )
⎡ tan θ + µ s ⎤
= rg ⎢
⎥ .
1 / cos θ
⎣ 1− µ s tan θ ⎦
(5)
b)
θ
Min Speed
N
k̂
r̂
θ
r
fs
N
s
=µ
mg
At minimum speed, the car is in danger of sliding down the incline and motion is impending.
Summing vertical forces
N cosθ + µ s N sin θ − mg = mavert = 0 ,
(6)
and
N ( cosθ + µ s sin θ ) = mg .
S 5-34
(7)
Summing the radial forces we find
2
mvmin
−N sin θ + µ s N cosθ = −
,
r
mv2min
N ( sin θ − µs cos θ ) =
.
r
and
(8)
(9)
Dividing equation (7) by equation (9) yields
N ( cosθ + µ s sin θ )
N ( sin θ − µs cos θ )
and
vmin =
=
mg
rg cos θ + µ s sinθ
= 2 =
,
2
mvmin / r vmin sin θ − µs cosθ
(10)
rg ( sinθ − µs cosθ ) 1 / cosθ
(cos θ + µs sinθ )
5-40)
m
h
⎡ tan θ − µs ⎤
= rg ⎢
⎥
1 / cosθ
⎣ 1 + µs tanθ ⎦
to = vo = 0
fAR
t
mg

v
A small sphere of mass m is released from rest at a great distance h above the ground, as
represented in the diagram above. Assume that the g is constant over this height and that the
magnitude of the air resistance is constant, proportional to the speed v , and given by
fAR = γ v ,
where γ is a positive constant of proportionality. Use Newton’s second law to derive an for the
acceleration of the sphere. Set up an appropriate differential equation and solve it; showing that the
speed of the sphere increases according to
(
)
v = vT 1− e − γ t /m ,
where vT is the so-called terminal velocity and given by
vT = mg / γ .
We can write
and
Rearranging terms,
and
ma = mg − γ v ,
dv
γ
γ ⎡ mg
⎤
a=
=g− v= ⎢
− v⎥ .
dt
m
m⎣ γ
⎦
dv
γ
= dt ,
(mg / γ ) − v m
S 5-35
(1)
(2)
(3)
dv
γ
=
∫ mg / γ ) − v m ∫ dt .
v =0(
t =0
v
o
Let
t
o
s = ( mg / γ ) − v .
(5)
ds = −dv ,
(6)
Then
and our integrals become
(mg / γ )−v
∫
mg /γ
So,
(4)
ds
γ t
= − ∫ dt .
s
m0
(7)
⎡ ( mg / γ ) − v ⎤
⎡ γv⎤
γ
ln ⎢
=− t,
⎥ = ln ⎢1 −
⎥
m
⎣ mg ⎦
⎣ mg / γ ⎦
γv
1−
= e−γ t /m .
mg
γv
1 − e−γ t/ m =
,
mg
mg
v=
1 − e− γ t/ m .
γ
and
Further,
(
and, finally,
(8)
(9)
(10)
)
(11)
5-41)
m
r̂
b
M
R
r=
R2 + b 2
k̂
dϕ
ϕ̂
dM
r̂⊥
Derive an equation for the magnitude of the gravitational force exerted on a particle of mass
m at a point a vertical distance b above the center of a uniform circular mass distribution of radius
R and mass M , as represented in the diagram above. What happens to the form of this
expression when b >> R ?
We first calculate the gravitational field produced by the circular mass distribution at mass
m . We have
S 5-36
 GdM
dg = 2 r̂ .
r
(1)
M
⎡ M ⎤
dM = λ d = ⎢
Rd
ϕ
=
dϕ .
⎥
2π
⎣ 2π R ⎦
(2)
The infinitesimal mass is given by
The unit vector r̂ is given by
r̂ = − cos θ k̂ + sin θ r̂⊥ .
(3)
By symmetry, we can ignore the r̂⊥ term. So, we have
⎞
GM dϕ ⎛
b
 G ( M / 2π ) dϕ
dg =
−cos
θ
k̂
=
−
k̂
⎟
R2 + b 2
2π R 2 + b 2 ⎜⎝
R2 + b 2 ⎠
GMb =−
dϕ k̂ .
2
2 3/2
2π R + b
(
)
(
(
)
Therefore,


g = ∫ dg = −
GMb )
2π
(4)
GMb k̂ .
(5)
2
2 3/ 2 ∫
2
2 3/2
2π R + b
R
+
b
0
The gravitational force on point mass m is given by
G
GMmb

FmM
= mg = − 2
k̂ .
(6)
2 3/2
R +b
For b >> R , we first rewrite equation (6) as
G
GMmb
GMm
FmM = −
k̂
≈
−
k̂ .
(7)
3/2
b2
⎡ b2 1 + R 2 / b2 ⎤
⎣
⎦
5-42) A binary star system consists of two stars of mass m1 and m2 that are in circular orbits of
radii r1 and r2 about the center of mass of the system; a point called the barycenter center. This
(
dϕ k̂ = −
)
(
( (
(
)
)
))
physical state of affairs is represented in the diagram below. Use Newton’s second law and law of
universal gravitation to show that
4π 2
(r1 + r2 )3 .
τ =
G (m1 + m2 )
2
For m1 , we have
−
and
Gm1 m2
(r1 + r2 )2
m1 (2π r1 / τ )
4π 2 m1r1
=−
=−
,
r1
τ2
2
Gm2
(r1 + r2 )2
4 π 2 r1
= 2 .
τ
S 5-37
(1)
(2)
In a similar fashion, for mass m2 we can write
Gm1
(r1 + r2 )2
4 π 2 r2
=
.
τ2
Adding equations (2) and (3) we find
Gm2
+
Gm1
(r1 + r2 )2 ( r1 + r2 )2
and
G
(r1 + r2 )2
Therefore,
(3)
4π 2 r1 4π 2 r2
=
+
,
τ2
τ2
4π 2
(m1 + m2 ) = 2 (r1 + r2 ) .
τ
⎡
⎤
4π 2
3
τ =⎢
⎥ (r1 + r2 ) .
⎣ G ( m1 + m2 ) ⎦
2

v2
m2
r2
c.m.
r1
m1

v1
S 5-38
(4)
(5)
(6)
Solutions to Problems for Chapter Six
6-1) A truck of mass M = 10 kg moves with speed u = 30 m / s . Do the following:
4
Calculate the speed at which a car of mass m = 12 × 10 kg would have to travel
to have the same linear momentum as the truck.
b)
Calculate the speed at which the car would have to move to have the same kinetic
energy as the truck.
a) We require,
pc = mv = pT = Mu ,
(1)
and, therefore,
2
a)
⎡M
v=⎢
⎣m
b)
⎤
⎥u =
⎦
⎡ 10 4 kg ⎤
⎢ 12 ×10 2 kg ⎥ ( 30 m / s ) = 250 m / s .
⎣
⎦
(2)
We require,
Kc =
and, therefore,
v=
M 2
u =
m
1 2
1
2
mv = K T = Mu ,
2
2
(3)
M
10 4 kg
u =
( 30 m / s ) = 86.6 m / s .
m
12 ×10 2 kg
(4)
6-2) An object initially at rest explodes into three pieces of equal mass. One piece moves east at
20 m / s . A second piece moves northwest at 20 m / s . Calculate the velocity of the third
piece.
As an explosion is the result of internal forces, the net external force is zero and the linear
momentum is conserved during the brief time interval over which the explosion takes place.
Therefore,




po = 0 = pL = px = p y .
(1)
()
north ˆj
u
45°
θ
v
m
u
m
()
east î
m
The conservation of linear momentum requires

px = 0 = mu − mu cos 45° − mv x .
Therefore,
S 6-1
(2)
v x = u − u cos 45° = u (1 − cos 45°) = ( 20 m / s ) (1 − cos45°) = 5.86 m / s .
Also required
Therefore,

py = 0 = mu sin 45° − mv y .
(4)
v y = u sin 45° = ( 20 m / s ) sin 45° = 14.14 m / s .
(5)

v = ⎡⎣−5.86 î −14.14 ĵ ⎤⎦ m / s .
(6)

v = 5.86 2 +14.14 2 m / s = 15.6 m / s ,
(7)
Finally, then,
and
(3)
directed at an angle
⎡ 14.14 ⎤
θ = tan −1 ⎢
⎥ = 67.5°
⎣ 5.86 ⎦
below the negative branch of the x-axis.
(8)
6-3) An object of mass 10 kg with a velocity 6 m / s î explodes into two fragments of equal
mass, one of which has a velocity 2 m / s î − 1 m / s ĵ . Calculate the velocity of the second
fragment.
()
y ĵ
v1
m
2m
θ
u
()
x î
ϕ
m
v2
The conservation of linear momentum requires




pJBE = p JAE = 2mu î = mv1 + mv 2 .
(1)


mv1 = 2mu î − mv 2 ,
(2)
So,
and
{
}


v1 = 2u î − v2 = 2 ( 6) î − ⎡⎣ 2 î − 1 ˆj ⎤⎦ m / s = ⎡⎣10 î + 1 ˆj ⎤⎦ m / s .
(3)
6-4) A piece of putty of mass m = 0.500 kg is moving horizontally with a speed u = 6 m / s
when it collides with and sticks to an initially stationary block on a frictionless surface. If 25%
of the kinetic energy of the putty is lost in the collision, what is the mass of the block?
This is an example of a completely inelastic collision. So, the linear momentum is conserved
S 6-2
and kinetic energy is lost. The conservation of linear momentum requires
mu = ( m + M ) v ,
and
(1)
(mu )2 = ( m + M )2 v2 .
(2)
JBC
m
JAC
m
u
v
M
M
The kinetic energy conditions require
while
3 ⎡1
1
2⎤
mu
=
(m + M ) v 2 ,
⎢
⎥
4 ⎣2
⎦ 2
(3)
3
⎡⎣ mu 2 ⎤⎦ = ( m + M ) v 2 .
4
(4)
Division of equation (2) by equation (4) gives us
( mu )2
(m + M )2 v 2
4
=
= (m + M ) = m
2
3
m + M )v
3
⎡ mu2 ⎤ (
4⎣
Therefore,
M=
.
(5)
⎦
4
1
1
m − m = m = (0.500 kg) = 0.167 kg .
3
3
3
(6)
6-5) A car of mass m1 = 1,000 kg is at rest at a stoplight when struck in the back by another car
of mass m2 = 1,400 kg . The cars couple together and leave skid marks 4 m long. The
coefficient of kinetic friction is µk = 0.60 . Do the following:
a)
Calculate their common speed just after collision.
b)
Calculate the speed with which the second car struck the stationary car.
a)
JBC
m2
u
JAC
m1
m2
m1
v
The conservation of linear momentum requires
m2u = ( m1 + m2 ) v ,
and, therefore,
S 6-3
(1)
⎡ m + m2 ⎤
u=⎢ 1
⎥v .
⎣ m2 ⎦
(2)
Just after the collision, the forces acting on the coupled cars are represented in the free-body
diagram below.
y
N
m2
fk
m1
x
(m1 + m2 ) g
Summing y forces yields
N − ( m1 + m2 ) g = ( m1 + m2 ) ay = 0 → N = ( m1 + m2 ) g .
(3)
Summing x forces gives us
− µk ( m1 + m2 ) g = (m1 + m2 ) a x → a x = −µ k g .
(4)
As this acceleration is constant, we can write
0 = v 2 + 2ax  → v = −2ax  = 2 µ k g .
(5)
Therefore, substitution of equation (5) into equation (2) results in
⎡ m + m2 ⎤
⎡ m1 + m2 ⎤
u=⎢ 1
v
=
⎥
⎢
⎥ 2 µk g
⎣ m2 ⎦
⎣ m2 ⎦
m
⎡ 1, 000 +1,400 ⎤
−2
(
)
(
)
=⎢
2
0.6
9.810 m
⋅
s
4 m
=
11.8 . ⎥⎦
1,400
s
⎣
(
The speed just after collision is
(
)
)
v = 2µ k g = 2 (0.6 ) 9.810 m ⋅ s−2 (4 m ) = 6.86 m / s .
6-6) A neutron at rest decays into a proton, an electron and a neutrino.
If the linear momentum of the proton is 3 ×10
(
1
0
(6)
(7)
n → 11 p + e− + ν −24
kg ⋅ m / s at 37° N of E and the linear
−24
momentum of the electron is 4 ×10 kg ⋅ m / s at 53° S of W . Calculate the linear
momentum of the neutrino.
As the neutron was at rest when it decayed, the conservation of linear momentum requires



pp + pe− + pν = 0 .
(1)
So,
(
) (
)



pν = − ⎡⎣ pp + pe− ⎤⎦ = − ⎡⎣ 2.4 î + 1.8 ĵ + −2.4 î − 3.2 ĵ ⎤⎦ ×10 −24 kg ⋅ m / s
= 1.4 × 10−24 kg ⋅ m / s ĵ .
(2)
S 6-4
)
()
north ˆj

pp

pν
()
37°
ϕ
53°
east î

pe−
Ra , decays into a radon nucleus, 222
84 Rn by emitting an
α particle, 24 He (helium nucleus). The kinetic energy of the α particle is 6.72 ×10 −13 J . Do
6-7) A nucleus of radioactive radium,
226
86
the following:
a)
Calculate the so-called recoil speed of the radon nucleus.
b)
Calculate the kinetic energy of the radon nucleus.
(In the notation used above, the superscripts signify the so-called baryon number--the sum of the
number of protons and neutrons This number is used to approximate the mass of the nucleus--the
product of the number of baryons and the baryon mass. The baryon mass is the average between
−27
the mass of the proton and neutron--1.674 ×10 kg . The subscripts signify the electric charge
in terms of e , the magnitude of the electric charge of the proton and electron--1.602 × 10
In all nuclear reactions, both the baryon number and the charge number are conserved!)

pα
−19
C.

pRn
The conservation of linear momentum requires
mα u = mRn v ,
(1)
⎡ 4mbaryon ⎤
⎡m ⎤
⎛ 2 ⎞
v = ⎢ α ⎥u = ⎢
u.
⎥ u = ⎜⎝
111⎟⎠
⎢⎣ 222mbaryon ⎥⎦
⎣ mRn ⎦
(2)
and,
The kinetic energy of the alpha particle is given by
Kα =
1
2
mα u → u =
2
Therefore, using (3) in (2) gives us
S 6-5
2Kα
.
mα
(3)
2 2K α
v=
=
111 mα
(
) = 2.55 × 10
(111) (4 ⋅1.674 × 10 kg )
8 6.72 ×10 −13 J
−27
2
5
m
.
s
(4)
So, the kinetic energy of the radon nucleus is given by
K Rn =
(
(
)
kg) (2.55 ×10 m / s )
1
1
2
2
2
mRn v = 222mbaryon v = 111mbaryonv
2
2
= 111 1.674 ×10 −24
5
2
= 1.21 ×10 −14 J .
(5)
6-8) A meteor of mass 5 × 10 kg moving relative to a “stationary” Earth with speed
10 km / s strikes the Earth head-on.
8

v
m
M⊕
Do the following:
24
a)
Calculate the recoil speed of the Earth. ( M ⊕ = 5.97 × 10 kg )
b)
Calculate the kinetic energy “lost” in the collision. Express your answer in megatons
9
of TNT. (One ton of TNT is equivalent to 4.2 × 10 Joules .)
a) We treat this as a completely inelastic collision. So, the conservation of linear momentum
requires
mv = m + M ⊕ vr .
(1)
(
)
Therefore, the recoil speed vr is given by
⎡
5 × 10 8 kg
⎤
vr = ⎢
(10, 000 m / s ) = 8.38 × 10 −13 m / s .
8
24
⎥
⎣ 5 × 10 kg + 5.97 × 10 kg ⎦
b)
(2)
The change in kinetic energy is given by
ΔK = K L − K o =
=
(
)(
1
⎡⎣( m + M⊕ ) vr2 − mv 2 ⎤⎦
2
) (
)
1⎡
2
8
24
−13 2
8
5 ×10 + 5.97 ×10
8.38 × 10
− 5 × 10 (10,000 ) ⎤ J
⎦
2⎣
= −2.5 × 1016 J ≡ a loss of 5.95 × 106 tons = −5.95 Mtons .
S 6-6
(3)
6-9)
M

u
m
A projectile of mass m = 200 grams strikes a stationary block of mass M = 1.3 kg with
a speed u = 30 m / s , as represented in the diagram above. The projectile embeds in the block.
Do the following:
a)
Calculate the height above the platform to which the block will rise before falling back
down.
b)
Calculate the “loss” of kinetic energy in the collision.
c)
Speculate as to “where” that energy went.
a) We have another completely inelastic collision. So, the conservation of linear momentum
requires
mu = ( m + M ) v ,
(1)
and
⎡ m
v=⎢
⎣m+M
⎤
⎡ 0.2 ⎤
u
=
⎥
⎢ 0.2 + 1.3 ⎥ ( 30 m / s ) = 4 m / s .
⎦
⎣
⎦
(2)
After the collision, the only force acting on the block is the “constant” gravitational force.
So, we can write
0 = v 2 − 2gh ,
(3)
and, therefore,
( 4 m / s )
v2
h=
=
= 0.815 m .
2g 2 9.810 m ⋅ s −2
2
(
b)
(4)
The change in kinetic energy is given by
ΔK = K L − K o =
=
c)
)
1
⎡⎣( m + M ) v2 − mu 2 ⎤⎦
2
1
⎡( 0.2 + 1.3) (4 )2 − (0.2 )( 30 )2 ⎤ J = −78 J .
⎦
2⎣
(5)
The energy lost during the collision went into some sound and some material deformation.
S 6-7
Solutions to Problems for Chapter Seven
7-1) A turntable of diameter 30.48 cm starts from rest and takes two seconds to reach its final
rotational rate of 33.3 RPM . Do the following:
a)
Assuming it constant, calculate the angular acceleration of the turntable.
b)
Calculate the number of revolutions the turntable has made five seconds after its startup.
c)
Calculate the time needed, from startup, to complete two revolutions.
d)
Calculate the radial and tangential accelerations of a point on the rim of the turntable at:
i)
t = 1 s ,
ii) t = 3 s .
a)
For constant angular acceleration,
α = α ave =
Δω ⎡⎣ 33.3 ( 2π rad / s ) / (60 s )⎤⎦
=
= 1.754 rad / s 2 .
Δt
2 s
(1)
b) In the first five seconds, the turntable accelerates for two seconds and rotates with a constant
angular speed for three. So, the total angular displacement is given by
Δϕ = Δϕ a + Δϕc
⎛ t a2
⎞
⎡1 2 ⎤
⎡
⎤
= ⎢ α ta ⎥ + ⎣ (α ta ) tc ⎦ = α ⎜ + ta tc ⎟
⎝2
⎠
⎣2
⎦
⎛ (2s )2
⎞
14.03 = 1.754 rad / s ⎜
+ ( 2s )( 3s )⎟ = 14.03 rad ≡
rev = 2.23 rev .
2π
⎝ 2
⎠
(
2
)
(2)
c) From our results, we can see that the time will be a little less than five seconds. So, the total
elapsed time will be the sum of the time for acceleration and the time need at constant angular
speed. During the two second acceleration, the number of revolutions completed is given by
(
)
1.754 rad / s 2 ( 2s )
Δϕa
α t a2
=
=
= 0.558 rev .
2π
2 ( 2π )
4π
2
(3)
So the time needed to complete the remaining revolutions is given by
⎛ 33.3 rev⎞
2 rev − 0.558 rev = 1.442 rev = ⎜
t .
⎝ 60 s ⎟⎠ c
(4)
Therefore, the total elapsed time to complete two revolutions is given by
⎡
⎛ 60 s ⎞ ⎤
t = (2 s ) + ⎢1.442 rev⎜
= 4.60 s .
(5)
⎝ 33.3 rev ⎟⎠ ⎥⎦
⎣
At time t = 1 s , the turntable is still accelerating so it has both radial and tangential
c) i)
accelerations given, respectively, by
(
)
2

2
arad = Rω 2 = R (α t ) = (0.1524 m ) ⎡⎣ 1.754 rad / s 2 (1s )⎤⎦ = 0.469 m / s 2 , (6)

and
atan = Rα = (0.1524 m ) 1.754 rad / s2 = 0.267 m / s2 .
(6)
(
)
ii) At time t = 3 s , the turntable is rotating at a constant 33.3 RPM , so there is no
tangential acceleration. The radial acceleration is
S 7-1
2

⎡
⎛ 2π rad ⎞ ⎤
arad = Rω 2 = ( 0.1524 m ) ⎢ 33.3 ⎜
= 1.857 m / s 2 .
⎟
⎥
⎝ 60 s ⎠ ⎦
⎣
(7)
7-2) Assume the Earth’s axis of rotation is parallel to it orbital axis of rotation. The Earth spins
about its own axis in the same sense it orbits the Sun.

v
Do the following:
a)
Calculate the spin angular speed of the Earth about its own axis.
b)
Calculate the average orbital speed of the Earth in its orbit of the Sun.
c)
At perihelion, the Earth passes closest to the Sun. It moves fastest at this point,
instantaneously on a circular orbit of radius R p . At aphelion, the Earth is at its farthest
point from the Sun, instantaneously on a circular orbit of Ra . The distance between
these two points is given by
R p + Ra = 2a = 2.992 ×1011 m ,
Ra 1 + ε
=
,
Rp 1 − ε
while
where ε , the eccentricity of the Earth’s orbit, is measured be ε = 0.0167 . Use this
information to calculate the orbital angular speed of the Earth at perihelion and
aphelion.
Ra
εa
RP

va
M
M ⊕ a (1 − ε )

vp
a (1 + ε )
M⊕
a
a)
For constant angular speed, we have
ω rot = ω rot ,ave =
Δϕ
2π rad
−5
=
= 7.27 × 10 rad / s .
Δt 24 (3,600 s )
S 7-2
(1)
b) Recall that planets orbit the Sun on elliptical paths, where the Sun is located at one of the foci
and the average distance of the planet from the Sun is the semi-major axis of the ellipse, signified
by a . The Sun is “off” center by a distance ε a , where ε is called the eccentricity and is a
particular feature of the planet’s particular orbit. When the planet is closest to the Sun it is said to
be at perihelion and, instantaneously moving on a circular path of radius R p = a (1− ε ) . When
the planet is furthest from the Sun, it is at aphelion and also instantaneously on a circular path.
However, at aphelion the radius is Ra = a (1 + ε ) . Average values are arrived at by treating the
planet as moving at constant speed on a circular path of radius a . So, the average orbital angular
speed of the Earth about the Sun is given by
ω orb =
(
vave 1 GM 
GM 
=
=
a
a
a
a3
)(
⎡ 6.67 × 10−11 N ⋅ m 2 ⋅ kg −2 1.99 × 1030 kg
=⎢
3
⎢
1.496 × 1011 m
⎣
(
)
)
1/2
⎤
⎥
⎥
⎦
= 1.99 × 10−7 rad / s .
(1)
Note that this is the same value as
ω orb =
c)
2π rad
−7
= 1.99 × 10 rad / s .
365 ( 24 )( 3,600 s )
(2)
At perihelion, the orbital radius is given by
RP = a (1 − ε ) .
(3)
Substitution of equation (3) into equation (1) gives us
ωp =
vp
=
a (1 − ε )
GM 
(a (1 − ε ))
= (1 − 0.0167 )
d)
−3/ 2
= (1− ε )
−3/ 2
3
(1.99 × 10
−7
GM 
−3/2
= (1 − ε ) ωorb
3
a
)
rad / s = 2.04 × 10−7 rad / s .
(4)
At aphelion,we have
ωa =
vp
=
a (1 + ε )
GM 
( a (1 + ε ))
= (1 + 0.0167 )
−3/ 2
= (1+ ε )
−3/ 2
3
(1.99 × 10
−7
)
GM 
−3/ 2
= (1 + ε ) ω orb
3
a
rad / s = 1.94 ×10 −7 rad / s .
7-3)
θ
S 7-3
r
R⊕
(5)
Find the linear speed of a point mass m on the surface of the Earth relative to the center of the
Earth at:
a)
Quito, Ecuador, roughly at the equator.
b)
New York at latitude 41° .
a)
Translational or linear speeds are related to angular speeds by
v = Rω rot .
(1)
The diagram above indicates that the radius of the circular path on which a person on the Earth
moves is given by
r = R⊕ cosθ ,
(2)
where θ is the latitude. So, in general, the translational speed is given by
v = R⊕ (cosθ ) ωrot .
(3)
At the equator, we would have
(
)
(
)
v = 6.378 × 10 6 m ( cos0°) 7.27 ×10 −5 rad / s = 364 m / s ≡ 1,040 mph . (4)
(The value one gets will depend on the radius used. The average radius of the Earth is
6.371 × 10 6 m while the equatorial radius is 6.378 ×10 6 m . I would accept either value.)
b) At latitude 41° we find
(
)
(
)
v = 6.378 × 10 6 m ( cos40° ) 7.27 × 10−5 rad / s = 350 m / s ≡ 783 mph . (5)
7-4) The angular position of a line segment on a disk of radius 6 cm is given by:
ϕ = ⎡⎣10 − 5t + 4t 2 ⎤⎦ rad .
ĵ
to

ϕo
î
6 cm
Do the following:
a)
Calculate the average angular speed of the disk over the time interval 1 to 3 s .
b)
Calculate the linear speed (same as the translational or tangential speed) at a point on
the rim of the disk at the time t = 2 s .
c)
Calculate the magnitude of the radial and tangential acceleration of the same point on
the disk at time t = 2 s .
a) The average angular speed is given by
S 7-4
Δϕ ϕ (t = 3s ) − ϕ (t = 1s )
=
Δt
2 s
2
⎡10 − 5 ( 3s ) + 4 (3s ) ⎤ rad − ⎡10 − 5 (1s ) + 4 (1s )2 ⎤ rad
⎦
⎣
⎦
=⎣
= 11 rad / s . (1)
2 s
ω ave =
b)
By definition, we write
dϕ
d
2
= R ⎡⎣10 − 5t + 4t rad ⎤⎦ = R [8t − 5] rad / s .
dt
dt
v (t = 2s ) = (0.06 m ) ⎡⎣ 8 ( 2 s ) − 5 ⎤⎦ rad / s = 0.66 m / s .
v = Rω = R
Therefore:
c) The magnitude of the radial acceleration is given by
v 2 (0.66 m / s )

2
arad =
=
= 7.26 m / s .
R
0.06 m
(2)
(3)
2
(4)
The magnitude of the tangential acceleration is given by
dω
d

2
atan = R α = R
= R [8t − 5] rad / s = R 8 rad / s
dt
dt
(
(
)
)
= (0.06 m ) 8 rad / s2 = 0.48 m / s2 .
(5)
7-5) A particle moves on a circle of radius r with angular speed ω and angular acceleration α .
Show that the magnitude of the total translational acceleration is given by

a = r ω4 +α2 .
We have

a =
 2 
arad + atan
2
=
( rω ) + ( rα )
2 2
2
(
)
= r 2 ω 4 + α2 = r ω4 + α2 .
(1)
7-6) At time t = 0 , a flywheel of radius R is rotating at 50 RPM . A motor gives the flywheel
2
a constant angular acceleration α = 0.5 rad / s until it reaches 100 RPM , at which time the
motor is disconnected. Calculate the number of revolutions of the flywheel in the interval t = 0 to
t = 20 s .
As the angular acceleration is constant, we can write
ω = ω o + α ta ,
(1)
where we have used to = 0 . Therefore,
2ω o − ω o
ω
50 ( 2π rad / 60 s )
= ta = o =
= 10.472 s .
α
α
0.5 rad / s 2
(2)
The total angular displacement, then, is made up of a period when the flywheel is accelerating
and a period when there is no angular acceleration. We can write
(
(
Δϕ = Δϕ a + Δϕc
)
= ωo ta + (1 / 2 )αt a2 + ( 2ωo )(20 − ta ) = (1 / 2) αt a2 + ω o (40 − ta )
)
= (1 / 2) 0.5 rad / s 2 (10.472 s ) + ( 50 ( 2π / 60 ) rad / s )( 40 −10.472 s ) = 182 rad
2
S 7-5
≡
182 rev = 29 rev .
2π
(3)
7-7) A car with tires of radius 30 cm starts at rest and reaches a speed of 108 km / hr in ten
seconds. Do the following:
a)
Calculate the angular acceleration of the wheels.
b)
Assuming no slipping, calculate the number of revolutions the wheel makes in the ten
second interval.
c)
For a point on the rim of a wheel, with respect to the center of the wheel, calculate the
the magnitude of the radial acceleration at the instant the speed of the wheel is
100 km / hr .
d)
Calculate the magnitude of the tangential acceleration of a point on the rim of a wheel
at the instant the speed of the wheel is 100 km / hr .
e)
Calculate the total acceleration of the point on the rim described in parts d) and e) and
determine the value of the angle the total acceleration vector makes to the radial direction
at this instant.
a) Assuming the angular acceleration is constant, we have
α = α ave =
b)
c)
Δω ⎡⎣108 (1000 m ) / ( 3,600 s ) ⎤⎦ − 0
2
=
= 3.00 rad / s .
Δt
10 s
For constant angular acceleration
We have
(
)
Δϕ = ω o t + (1 / 2 )α t 2 = 0 + (1 / 2 ) 3 rad / s 2 (10 s )
150
= 150 rad ≡
rev = 23.9 rev .
2π
(1)
2
v 2 ⎡⎣100 (1,000 m / 3,600 s )⎤⎦

2
arad =
=
= 2,570 m / s .
R
0.30 m
(2)
2
d)
We can write
(
(3)
)

atan = Rα = (0.30 m ) 3 rad / s 2 = 0.90 m / s 2
e)

atan

arad

a
θ
100 km / hr
We write
θ = tan
−1

atan
−1 0.90
= 0.019° .
 = tan
arad
2,570
S 7-6
(4)
7-8) The angular position of a rotating disk is given by
θ = ( 2t − 5t 2 + 2t 4 ) rad .
Do the following:
a)
Calculate the angular acceleration of the disk at time t = 1 s .
b)
Calculate the average angular acceleration between t = 1 s and t = 2 s .
a)
The angular velocity is defined by
ω=
dθ d
2
4
3
=
2t − 5t + 2t rad = 2 − 10t + 8t rad / s .
dt dt
(1)
dω d
3
2
2
=
2 − 10t + 8t rad / s = 24t − 10 rad / s .
dt
dt
(2)
(
)
(
)
The angular acceleration, then, is given by
α=
Therefore,
b)
(
)
(
(
)
)
α (t = 1) = 24 (1) − 10 rad / s 2 = 14 rad / s 2 .
2
(3)
The average acceleration is defined by
Δω ω (t = 2 ) − ω (t = 1)
=
Δt
Δt
3
⎡ 2 −10 (2 ) + 8 (2 ) − 2 −10 (1) + 8 (1)3 ⎤ rad / s
⎦
=⎣
= 46 rad / s 2 .
1s
α ave =
(
) (
)
(4)
7-9) A wheel of radius R = 0.200 m is rotating at an angular frequency of 120 RPM . In the
next minute it makes 90 revolutions. Do the following:
a)
Calculate the constant angular acceleration.
b)
Calculate how much more distance the wheel will travel before coming to rest.
c)
Calculate the magnitude the radial and tangential accelerations of a point on the rim of
the wheel at the instant it begins its last revolution.
a)
For constant angular acceleration, we can write
90 rev ≡ 565.5 rad = Δϕ = ωo t + (1 / 2 )α t 2 ,
and
α=
2 ( Δϕ − ω ot )
t
2
=
2 ⎡⎣ 565.5 rad − (12.57 rad / s )(60 s ) ⎤⎦
(60 s )
2
(1)
=− 0.105 rad / s . (2)
2
So, at the end of this sixty second interval, the wheel has an angular speed given by
ω = ω o + α t = (12.57 rad / s ) + (− 0.105 rad / s 2 ) (60 s ) = 6.27 rad / s .
b)
and
(3)
As the angular acceleration is constant, we can write
ω 2 = 0 = ω 2o + 2α (Δϕ ) = ω 2o + 2α (Δr / R ) ,
(4)
Rωo2
Δr = −
,
2α
(5)
S 7-7
where we have used
Δr = R Δϕ .
(6)
Of course, in equation (5), ω o is the angular speed at the end of the interval we used earlier to
calculate the angular acceleration; the value given by equation (3). So, equation (5) becomes
Δr = −
(0.20 m )( 6.27 rad / s )2
= 37.4 m . (7)
2 −0.105 rad / s 2
c) In one revolution, the wheel rotates 2π rad . So, we can find the angular speed of the wheel at
(
)
the instant it begins its last revolution. We have
ω = ω o2 + 2α (( Δr / R ) − 2π )
=
( 6.27 m / s )2 + 2 (−0.105 rad / s 2 )(( 37.4 / .2 ) − 2π ) rad = 1.17 rad / s .
Therefore:

2
arad = Rω 2 = ( 0.20 m) (1.17 rad / s ) = 0.27 m / s 2 .
The magnitude of the tangential acceleration is
(
)

atan = R α = ( 0.20 m) 0.105 rad / s2 = 0.021 m / s 2 .
(8)
(9)
(10)
7-10) A wheel makes 40 revolutions in five seconds and, at the end of this time interval, rotates at
100 RPM . Calculate the constant angular acceleration.
In the absence of any information about initial conditions, I assume the initial angular speed is
zero. We have then, for constant angular acceleration
ω = ωo + αt = 0 + αt = αt ,
(1)
and
α=
We know also that
ω 100 ( 2π rad / 60 s )
2
=
= 2.09 rad / s .
t
5 s
(
)
(2)
Δϕ = ω o t + (1 / 2 )α t 2 = 0 + (1 / 2 ) 2.09 rad / s 2 (5 s ) = 26.2 rad
26.2
≡
rev = 4.16 rev .
(3)
2π
Clearly not 40 rev ! You know what they say about assumptions! It is back to the drawing board
2
with an initial angular speed assumed. (Oh no, another assumption. However, we have some
information now that suggests it is the better assumption.)
What we require is something that satisfies two equations. First, we note that if
ω = ωo + αt ,
(4)
then
ωo = ω − αt ,
(5)
and, therefore,
Δϕ = (ω − αt ) t + (1 / 2 )α t 2 = ωt − α t 2 + (1 / 2 )α t 2 = ωt − (1 / 2 )α t 2 .
(6)
Therefore,
S 7-8
α=
2 (ω t − Δϕ ) 2 ⎡⎣(100 ( 2π rad / 60 s ) (5 s )) − ( 40 )( 2π rad)⎤⎦
rad
=
= −16 2 . (7)
2
2
t
s
(5 s )
7-11) Find the magnitude of the linear acceleration of an astronaut in:
a)
a centrifuge of radius 15 m and that has an angular speed 1.2 rad / s and an
2
angular acceleration 0.8 rad / s .
ω
R
b)
a doughnut shaped space station of radius 1.0 km and that rotates at a constant
0.5 RPM .
Space - Station in Cross - Section
ω
R
a)
Using the results of problem 7-5), we can write
(
)
1/2
2
4
a = R ω 4 + α 2 = (15 m ) ⎡ (1.2 rad / s ) + 0.8 rad / s 2 ⎤
⎣
⎦
b)
= 24.7 m / s2 . (1)
a = Rω 2 = (1, 000 m )(0.5 ( 2π rad / 60 s )) = 2.74 m / s 2 .
2
(2)
7-12) A car with tires of radius 25 cm accelerates from rest to 30 m / s in 10 s . When the
speed of the car is 12 m / s , find the linear acceleration of a point at the top of the wheel:
a)
relative to the center of the wheel;
b)
relative to the road.
a) To solve this problem we use the so-called Galilean transformation. To review, in the diagram
below, at some instant in time, a point P is on the circumference of a wheel of radius R that is on
a horizontal surface--the road. There is a Cartesian coordinate system fixed to the road. A second

Cartesian coordinate system parallel to the first is fixed to the center of the wheel. The vector rPR

represents the position of point P relative to the road. The vector rCR represents the position of
S 7-9

the center of the wheel relative to the road. The third vector rPC represents the position of point P
relative to the center of the wheel.

rPR
ĵ
ˆj ′
P

rPC
ˆi ′

rCR
î
The rules of vector addition require



rPR = rCR + rPC .
(1)
The velocities and accelerations are related in the same way.
while
d 





rPR = rCR + rPC ] = v PR = vCR + v PC ,
[
dt
(2)
d 





v PR = vCR + v PC ] = aPR = aCR + aPC .
[
dt
(3)
For a point at the top of the wheel, the instantaneous velocity relative to the center of the wheel
is, of course, tangent to the circle.

vPC
P

vCR
The center of the wheel, relative to the road has a constant acceleration given by
aCR =
( 30 m / s ) − 0
10 s
= 3.0 m
.
s2
(4)
For point P at the top, the magnitude of the radial acceleration is given by
2
⎛ (12 m / s )2 ⎞
m⎞
m
⎛
2
2
aPC = aPC,rad + aPC ,tan = ⎜
+ ⎜ 3.0 2 ⎟ = 576 2 .
(5)
⎟
⎝
s ⎠
s
⎝ 0.25 m ⎠
Now, with respect to the road, the magnitude of the acceleration of point P is given by
2
b)
S 7-10
2
2
aPR = aPC
+ aCR
2
2
m⎞
m
⎛
⎛ m⎞
= ⎜ 576 2 ⎟ + ⎜ 3 2 ⎟ = 576 2 .
⎝
⎝ s ⎠
s ⎠
s
S 7-11
(6)
Solution to Problems for Chapter Eight
8-1) Point masses m1 , m2 , m3 and m4 are related by mn = n kg . The positions of the point
masses are, respectively:
(3 m , 1 m) , (−2 m , 2 m ) , (1 m , −1 m ) and (−2 m , − 1 m ) ,
as represented in the diagram below. Recall that for a point mass, the moment of inertia is given by
I = mr⊥2 .
ĵ
m2
m1
î
m3
m4
Do the following:
a)
Calculate the total moment of inertia about the x-axis.
b)
Calculate the total moment of inertia about the y-axis.
c)
Calculate the total moment of inertia about the z-axis.
a)
b)
With respect to the x-axis, the perpendicular distance is the y-coordinate. We have
2
2
2
2
I x = ⎡⎣(1) (1) + ( 2) (2 ) + (3) (1) + ( 4 )(1) ⎤⎦ kg ⋅ m2 = 16 kg ⋅ m2 .
With respect to the y-axis, the perpendicular distance is the x-coordinate. We find
2
2
2
2
I y = ⎡⎣(1)( 3) + (2 )( 2 ) + ( 3)(1) + (4 ) (2 ) ⎤⎦ kg ⋅ m2 = 36 kg ⋅ m 2 .
(1)
(2)
c) With respect to the z-axis, the perpendicular distance is the magnitude of the position, the
hypotenuse of the right triangle for which the coordinated represent the length of the legs. We have
Iz = ⎡⎢ (1)
⎣
( 10 )
2
+ ( 2)
( 8)
2
+ ( 3)
( 2)
2
+ (4 )
( 5 ) ⎤⎦⎥ kg ⋅ m
2
2
= 52 kg ⋅ m 2 . (3)
8-2) Four equal point mass m are connected by thin, massless rods, as represented in the diagram
below. Calculate the moment of inertia of the system about the z-axis.
With respect to the z-axis, we have, moving clockwise around the point masses,
(
Iz = m ⎡⎢ a 2
⎣
)
2
(
)
2
2
+ (2a ) + a 2 ⎤⎥ kg ⋅ m 2 = m ⎡⎣ 2a 2 + 4a 2 + 2a2 ⎤⎦ kg ⋅ m 2
⎦
= 8ma 2 kg ⋅ m2 .
S 8-1
(1)
ĵ
k̂ out
of the page m

î
a
m
a
a
m
a
m
P 8-1
8-3) Four equal point mass m are connected by thin, massless rods, as represented in the diagram
below. Calculate the moment of inertia about the z-axis.
ĵ
m
a
a
k̂ out
of the page

m
î
m
a
a
m
With respect to the z-axis, we have, moving clockwise around the point masses,
(
2
Iz = m ⎡⎢( a) + a 2
⎣
)
2
2
+ (a ) ⎤⎥ kg ⋅ m 2 = 4ma2 kg ⋅ m 2 .
⎦
(1)
8-4) Represented in the diagram below, not drawn to scale, is a wheel that has a hub of radius r
and mass m , with four spokes of length R and mass m′ . The outer thin ring has a mass M and
radius R + r . Calculate the moment of inertia of the wheel about an axis that passes through the
center of the wheel perpendicular to the plane of the wheel if:
r = 2 m , m = 2 kg , R = 4 m , m ′ = 1 kg , and M = 2 kg .
For the hub, we have
S 8-2
Ihub =
1 2
mr .
2
(1)
R
R+ r
r
For the four spokes, we have a moment of inertia given by
1
⎡
2
2⎤
Ispokes = 4 ⎢ m ′r + m ′R ⎥ ,
3
⎣
⎦
(2)
Iring = M ( R + r ) .
(3)
where we have used the parallel axis theorem. Finally, for the ring,
2
The total then is
1 2
1
⎡
2
2
2⎤
mr + 4 ⎢ m′ r + m ′R ⎥ + M ( R + r )
2
3
⎣
⎦
1
2
⎡
2
2⎤
+ 4 ⎢ (1 kg )(2 m) + (1 kg) ( 4 m ) ⎥ + (2 kg )(( 4 m ) + (2 m ))
3
⎣
⎦
Itot =
=
1
(2 kg) (2 m )2
2
= 113 kg ⋅ m 2 .
(4)
8-5)
3R
R
m
R
m
m
Two solid spheres of mass m and radius R are connected to the ends of a thin rod of mass
m and length 3R , as represented in the diagram above. Calculate the moment of inertia of this
system about the axis shown. The axis bisects the “dumbbell.”
The moment of inertia of the thin rod about its center is given by
Ithin r od =
1
2
2
m ( 3R ) = (0.75 ) mR .
12
(1)
Using the parallel axis theorem, for the two spheres, we have
2
Ispheres = 2 ⎡⎣ m ( 2.5R ) + (2 / 5 ) mR2 ⎤⎦ = (13.3 ) mR2 .
S 8-3
(2)
Total, then, is given by
Itot = (14.05 ) mR2 .
(3)
8-6) A can is a hollow cylinder of radius R and height h , composed of a circular top and bottom
and a lateral surface. All parts of the can are made of a thin press of metal with uniform surface
mass density σ . This physical state of affairs is represented in the diagram below. Calculate the
moment of inertia of the can about the major axis of symmetry; the z-axis.
k̂
R
h
In a top view of a quarter of a circle, we have
y
dm
dA
r⊥ dϕ
dr⊥
dϕ
r⊥
x
The mass is “smeared” uniformly over a surface. So,
dm = σ dA = σ ( r⊥ dϕ )(dr⊥ ) = σ dϕ r⊥ dr⊥ ,
(1)
and the infinitesimal moment of inertia is given by
dI top,z = r⊥2 dm = σ dϕ r⊥3 dr⊥ .
Therefore
2π
(2)
R
⎡1 4 ⎤ 1
3
4
Itop,z = ∫ dItop ,z = σ ∫ dϕ ∫ r⊥ dr⊥ = σ ( 2π ) ⎢ R ⎥ = σπ R .
⎣4 ⎦ 2
0
0
(3)
So, the moment of inertia for the top and the bottom is
Itop&bot ,z = σπ R 4 .
We now need to find the moment of inertia of the lateral surface. We have
S 8-4
(4)
R
dm
dz dA
Rdϕ
For the lateral surface, we have
dm = σ dA = σ ( Rdϕ )( dz ) = σ R dϕ dz .
(5)
The infinitesimal moment of inertia of the lateral surface is given by
dI LS = r⊥2 dm = R 2 σ Rdϕ dz = σ R 3dϕ dz .
Therefore,
I LS = ∫ dILS = σ R
The total, then , is:
2π
3
(6)
h
∫ dϕ ∫ dz = σ R (2π )( h ) = 2σπ R h .
3
0
3
(7)
0
Itot = σπ R 4 + 2σπ R 3h = σπ R 3 [ R + 2h ] .
(8)
8-7) A uniform sphere of radius a has a concentric spherical cavity of radius b . Find the
moment of inertial about a diameter. The mass of the object is m .
k̂
a
b
m
We use the spherical coordinate infinitesimal volume element shown below. We have, for
the mass density,
ρ=
m
3m
=
.
(4 / 3) π a3 − b 3 4π a 3 − b 3
(
)
S 8-5
(
)
(1)
r sin θ dϕ
dr
dm = ρdVolume
r dθ
The infinitesimal volume is given by
dV = ( r sin θ dϕ )( r dθ ) (dr ) = dϕ sin θ dθ r 2 dr .
(2)
So,
dm = ρdV =
3m
dϕ sin θ r 2 dr
3
3
4π a − b
(
)
(3)
The perpendicular distance of the volume element from the axis of rotation is
r⊥ = r sin θ → r⊥2 = r 2 sin2 θ .
(4)
r⊥ dm
θ r
ϕ
I = ∫ r dm =
2
⊥
Therefore:
2π
3m
π
∫ dϕ ∫ sin
4π (a − b )
3
3
0
0
a
θ dθ ∫ r 4 dr .
(5)
(
(6)
3
b
Two of these integrals are trivial:
2π
∫ dϕ = 2π
a
, while
0
∫r
(
So,
dr =
b
However, to solve the third integral, we note
Further,
4
)
1 5
5
a −b .
5
)
sin3 θ = sin θ 1 − cos2 θ = sin θ − cos2 θ sin θ .
d
1
3
2
2
3
cos θ = −3cos θ sin θ → − cos θ sin θ dθ = d cos θ .
dθ
3
(
π
)
π
(
π
(
)
)
(7)
(8)
1
1
π
2 4
π
3
3
sin
d
θ
=
sin
θ
d
θ
+
d
cos
θ
=
−
cos
θ
+
cos
θ
=
2
−
= . (9)
∫
∫
∫
0
0
3
3
3
3
0
0
0
3
S 8-6
3m
2 a 5 − b5
⎡ 4⎤ ⎡1 5
5 ⎤
I=
[ 2π ] ⎢ 3 ⎥ ⎢ 5 a − b ⎥ = 5 m a 3 − b 3 .
4π a 3 − b 3
⎣ ⎦⎣
⎦
(
(
)
)
(9)
8-8)
R
b
a
A uniform disk of radius R has a hole of radius a drilled through it, as represented in the
diagram above. The center of the hole is a distance b from the center of the disk. Calculate the
moment of inertia about an axis passing through the center of the disk and perpendicular to the
plane of the disk. The mass of the object is m .
The mass is “smeared” over an area, so the surface mass density is given by
σ=
m
.
π R − a2
(
)
2
(1)
The hole is treated as a superposition of negative mass. We must also use the parallel axis theorem.
We have
1
1
⎡
⎤
⎡⎣σπ R 2 ⎤⎦ R 2 − ⎢ σπ a 2 b 2 + σπ a2 a2 ⎥
2
2
⎣
⎦
4
4
2 2
1
1 ⎡ R − a − 2a b ⎤
4
4
2 2
= σπ ⎡⎣ R − a − 2a b ⎤⎦ = m ⎢
⎥ .
2
2 ⎣
R2 − a 2
⎦
(
I=
)
(
)
(2)
8-9) The angular acceleration of an object is given by
α = (12t − 3t 2 ) rad / s2 .
The angular speed of the object is 10 rad / s at time t = 1 s and the angular displacement is
5 rad at time t = 2 s . Write expressions for the angular speed and angular displacement as
functions of time.
By definition, we have
α=
dω
2
2
2
2
= 12t − 3t rad / s → dω = dt 12t − 3t rad / s ,
dt
(
ω
and
)
t
(
t
∫ dω = 12 ∫ t dt − 3∫ t
ωo
0
boundary conditions require, at t = 1 :
2
(
)
(1)
)
(2)
dt → ω − ω o = 6t − t rad / s .
0
S 8-7
2
3
(
)
ω = 6 (1) − 13 + ωo rad / s = 10 rad / s ,
(3)
ω o = 5 rad / s .
(4)
2
and, therefore,
Similarly,
ω=
and
ϕ
dϕ
2
3
2
3
= 5 + 6t − t rad / s → dϕ = dt 5 + 6t − t rad / s ,
dt
(
t
)
t
(
)
t
1 4⎤
⎡
3
3
d
ϕ
=
5
dt
+
6
t
dt
−
t
dt
→
ϕ
−
ϕ
=
5t
+
2t
−
t rad .
o
∫
∫
∫
∫
⎢⎣
4 ⎥⎦
ϕo
0
0
0
Boundary conditions require, at t = 2
1
⎡
3
4⎤
ϕ = ⎢ϕ o + 5 (2 ) + 2 (2 ) − ( 2) ⎥ rad = 5 rad → ϕ o = −17 rad .
4
⎣
⎦
2
So:
ω = 5 + 6t − t 3 rad / s ,
2
(
)
ϕ = (−17 + 5t + 2t 3 − (1 / 4 ) t 4 ) rad .
while :
(5)
(6)
(7)
(8)
(9)
8-10) Find the moment of inertia of a hollow cone of mass m and height h and apex angle 2θ
about the central axis of symmetry. (See the diagram below.) Hint: incorporate the so-called slant
height.
θ θ
z r
⊥
h
dm = σ dArea
s
ds
dz
m
R
In a moment, we will write the infinitesimal lateral surface area. If one integrates it over the
entire lateral surface of a right circular cone, one finds
ALS = π Rs ,
(1)
where R is the radius of the circular base of the cone and s is the so-called “slant height” of the
cone, and can be written as
s = R / sinθ .
(2)
So, the surface mass density of the cone is given by
S 8-8
σ=
The infinitesimal mass is given by
dm = σ dA =
and
m
m sin θ
=
.
π Rs
πR2
(3)
m sinθ
m sin θ
dz
2m tanθ
2
π
r
ds
=
2
π
r
=
r⊥ dz ,
⊥
⊥
π R2
π R2
cosθ
R2
dI = r⊥ dm =
2
We next note that
2m tanθ 3
r⊥ dz .
R2
(4)
(5)
3
r⊥ R
⎛ R⎞
⎛ R⎞
= → r⊥ = ⎜ ⎟ z → r⊥3 = ⎜ ⎟ z 3 ,
⎝ h⎠
⎝h⎠
z h
(6)
and equation (5) becomes
2m tanθ ⎛ R ⎞ 3
2mR tan θ 3
2mtan 2 θ 3
dI = r dm =
z dz =
z dz =
z dz .
R 2 ⎜⎝ h ⎟⎠
h3
h2
3
2
⊥
(7)
Therefore,
2m tan 2 θ 3
⎡ 2m tan2 θ ⎤ ⎡ 1 4 ⎤ 1
2
2
I = ∫ dI =
z dz = ⎢
h ⎥ = mh tan θ .
2
∫
2
⎥
⎢
h
h
⎣
⎦ ⎣4 ⎦ 2
0
h
(8)
8-11) At time t , a point mass m = 4 kg is at a position given by

r = −3 m î + 1 m ˆj ,
with a velocity given by

v = 1.286 m / s î + 1.532 m / s ĵ .
With respect to the origin of the Cartesian coordinate system in which the position and velocity
were measured, calculate the angular momentum of the point mass.
The angular momentum of a point
 mass is given by
 
 
L = r × p = m[ r × v ] .
(1)
Note that both the position and velocity vectors lie in the x-y plane. The cross product produces a
vector perpendicular to both vectors crossed. Therefore, the angular momentum must be parallel to
the z-axis and, therefore, given by

L = m rxv y − ryv x k̂
(
)
= ( 4kg ) ⎡⎣(−3 m ) (1.532 m / s ) − (1 m )(1.286 m / s )⎤⎦ k̂ = −23.5 kg ⋅ m 2 / s k̂ . (2)
8-12) At time t , a point mass m = 3 kg is at a position given by

r = 2 m î + 3 m ˆj ,
with a velocity given by

v = 0.500 m / s î − 0.866 m / s ĵ .
With respect to the origin of the Cartesian coordinate system in which the position and velocity
were measured, calculate the angular momentum of the point mass.
S 8-9
The angular momentum of a point
 mass is given by
 
 
L = r × p = m[ r × v ] .
(1)
Note that both the position and velocity vectors lie in the x-y plane. The cross product produces a
vector perpendicular to both vectors crossed. Therefore, the angular momentum must be parallel to
the z-axis and, therefore, given by

L = m rxv y − ryv x k̂
(
)
= ( 3kg ) ⎡⎣ (2 m ) (−0.866 m / s ) − ( 3 m )(0.50 m / s ) ⎤⎦ k̂ =− 9.70 kg ⋅ m 2 / s k̂ . (2)
8-13) At time t , a point mass m = 5 kg is at a position given by

r = −4 m î −2 m ĵ ,
with a velocity given by

v = 1.500 m / s î .
With respect to the origin of the Cartesian coordinate system in which the position and velocity
were measured, calculate the angular momentum of the point mass.
The angular momentum of a point mass
 is given by
 
 
L = r × p = m[ r × v ] .
(1)
Note that both the position and velocity vectors lie in the x-y plane. The cross product produces a
vector perpendicular to both vectors crossed. Therefore, the angular momentum must be parallel to
the z-axis and, therefore, given by

L = m rxv y − ryv x k̂
(
)
= (5kg ) ⎡⎣(−4 m )( 0) − (−2 m )(1.50 m / s )⎤⎦ k̂ = 15.0 kg ⋅ m 2 / s k̂ .
(2)
8-14)
k̂
ω
a
m
A solid sphere of mass m and radius a spins with a constant angular speed ω about a vertical
axis, as represented in the diagram above. Do the following:
a)
Derive an expression for the rotational kinetic energy of the sphere.
b)
Derive an expression for the angular momentum of the sphere.
c)
Derive an expression for the rotational kinetic energy as a function of the angular
momentum and the moment of inertia.
S 8-10
Calculate the rotational quantities of interest for the Earth, I , K rot , L . Assume the
Earth is a uniform solid sphere. (Of course, it is not.)
M ⊕ = 5.97 × 10 24 kg , R⊕ = 6.371 × 10 6 m , ω = 7.27 ×10 −5 rad / s .
The rotational kinetic energy is given by
d)
a)
K rot =
b)
c)
1 2 1⎛2
1
2⎞
2
2 2
Iω = ⎜ ma ⎟ ω = ma ω .
⎠
2
2⎝5
5
(1)
The angular momentum is given by
2 2
⎛2
2⎞
L = Iω = ⎜ ma ⎟ ω = ma ω .
⎝5
⎠
5
(2)
L2 = I 2ω 2 → ω 2 = L2 / I 2 .
(3)
1 2 1 ⎛ L2 ⎞ L2
= Iω = I ⎜ 2 ⎟ =
.
2
2 ⎝ I ⎠ 2I
(4)
Equation (2) implies
Equation (3) in equation (1) yields
K rot
d)
(
)(
)
2 2 2
2
24
6
37
2
ma = 5.97 × 10 kg 6.371 ×10 m = 9.69 × 10 kg ⋅ m ,
5
5
1
1
2
2 2
24
6
−5
K rot = ma ω = 5.97 × 10 kg 6.371 ×10 m 7.27 ×10 rad / s
5
5
= 2.56 × 1029 J .
2
2
2
2
24
6
−5
L = ma ω = 5.97 ×10 kg 6.371 × 10 m 7.27 × 10 rad / s
5
5
7.04 × 10 33 kg ⋅ m 2 / s . I⊕ =
(
)(
(
)(
)(
)(
(5)
)
2
(6)
)
(7)
8-15) In the Bohr model of the hydrogen atom, an electron of mass m and electric charge −e
orbits a stationary proton the electric charge of which is +e . The orbit is modeled as circular with
a radius r . The magnitude of the net radial electric force is given by
F E = ke 2 / r 2 ,
where k is a constant. In addition, Bohr assumed that the angular momentum of the electron was
quantized, restricted to only discrete values given by
mvr = nh / 2π ,
where h is Planck’s constant and n can be an integer n = 1, 2, 3, . Use the above information
to show that the nth possible orbit is given by
rn =
For circular motion, we have
( nh / 2π )2
mke 2
.
ke2 mvn2
ke 2
2
=
→ vn =
.
rn2
rn
mrn
Bohr’s quantization rule for the angular momentum yields
S 8-11
(1)
m v r = (n / 2π ) h → v =
2
2 2 2
n n
2
2
n
(n / 2π )2 h2
m 2 rn2
.
(2)
Equating the two results gives us
ke 2 (n / 2π ) h2
v =
=
.
mrn
m 2 rn2
2
2
n
So,
(3)
m2 rn2 (n / 2π ) h 2
(n / 2π ) h2
=
→ mrn =
.
mrn
ke 2
ke2
2
Therefore,
rn =
2
( n / 2π )2 h 2
It is more common to see this written as
mke 2
.
2
⎡ ( h / 2π ) 2 ⎤
⎤
2 ⎡ 
rn = n ⎢
⎥=n ⎢
2
2 ⎥ ,
⎢⎣ mke ⎥⎦
⎣ mke ⎦
where we have introduced a new term  , pronounced “h bar”, and defined by
 = h / 2π .
2
The so-called allowed orbits go as n . When n = 1 , the hydrogen atom is said to be in its
2
(4)
(5)
(6)
(7)
“ground state”. its lowest energy state. This radius for hydrogen is called the Bohr radius and has
a value of
rB = 5.29 × 1011 m .
(8)
8-16) A particle is executing uniform circular motion with speed v and angular speed ω . The
origin is on the axis of rotation but not at the center of the circle. Find
 the appropriate vector




quantities: a) v in terms of r and ω . b) arad in terms v and ω .
S 8-12
Solutions to Problems for Chapter Nine
9-1)
M
R
m1
m2
Two blocks of masses m1 = 3 kg and m2 = 5 kg are connected by a light string that
passes over a pulley of radius R = 8 cm and mass M = 4 kg , as represented above. The only
friction involved is that between the string and the pulley surface. Treat the pulley as a disk and its
center as the origin of a Cartesian coordinate system. Do the following:
a)
Calculate the net torque on the pulley.
b)
Calculate the angular momentum of the system at the instant the blocks have speed v .
c)
Calculate the magnitude of the acceleration of the blocks.
We always begin with a free-body diagram.

Fsupport
T1
T2
m1 g
m2 g
R
T1
T2
Mg
The blocks are moving translationally so we sum forces on the blocks and find, for block two,
m2 g − T2 = m2 a ,
(1)
T2 = m2 g − m2 a .
(2)
For block one,
T1 − m1 g = m1 a ,
(3)
and, also,
T1 − m1 g = m1 a .
(4)
As the pulley will rotate in the clockwise sense, m2 > m1 , tension two must be larger, and
and, also,
directed oppositely to tension one. So, we subtract tension one from tension two and find:
T2 − T1 = ( m2 g − m2 a ) − ( m1g + m1a ) = m2 g − m1 g − m2 a − m1 a .
(5)
The pulley rotates so we sum torques, finding the net torque is given by
RT2 − RT1 = Iα = ⎡⎣ (1 / 2 ) MR2 ⎤⎦ ( a / R ) = (1 / 2 ) MRa .
(6)
T2 − T1 = (1 / 2 ) Ma .
(7)
So, the difference in tensions is
Equating equations (5) and (7) gives us
and
(1 / 2 ) Ma = m2 g − m1 g − m2 a − m1 a ,
(m 2 + m1 + (1 / 2 ) M ) a = ( m2 − m1 ) g .
S 9-1
(8)
(9)
Therefore, the acceleration of the blocks is given by
⎡
⎤
m 2 − m1
a=⎢
⎥g
m
+
m
+
1
/
2
M
(
)
⎣ 2
1
⎦
⎡
⎤
5−3
=⎢
9.81 m ⋅ s−2 = 1.96 m ⋅ s −2 .
⎥
⎣ 5 + 3 + (1 / 2 ) 4 ⎦
(10)
Using equations (10) and (6), we find the net torque on the pulley is given by
Γ net = (1 / 2 ) MRa
(
)
= (1 / 2) (4 kg )( 0.08 m ) 1.96 m / s2 = 0.31 mN .
(11)
The angular momentum of the pulley at the instant the blocks are moving with speed v is, by
definition,
(
)
L = Iω = (1 / 2 ) MR 2 ( v / R ) = (1 / 2 ) MRv
= (1 / 2) (4 kg )( 0.08 m ) v = ( 0.16 ) v .
(12)
9-2)
M
R
m
A block of mass m = 2 kg hangs vertically from the rim of a pulley of mass M = 4 kg
and radius R = 20 cm , as represented above. Treat the pulley as a disk and its center as the
origin of a Cartesian coordinate system. Calculate the magnitude of the acceleration of the block.
Fsupport

R
T
T
Mg
mg
Again, as the block is moving translationally, to analyze its dynamics, we sum forces and get
mg − T = ma .
(1)
The rotational dynamics of the pulley are found by summing torques. The support force and the
S 9-2
gravitational force lines of action pass through the rotation axis so they produce no tension. Only
the tension produces a torque. So, we have
RT = Iα = ⎡⎣ (1 / 2 ) MR2 ⎤⎦ ( a / R ) ,
T = (1 / 2 ) Ma .
(2)
and
Substitution of equation (3) into a rearranged equation (1) yields
Therefore,
(3)
mg = ma + T = ma + (1 / 2) Ma = ( m + (1 / 2 ) M ) a .
⎡
⎤
m
a=⎢
⎥g
⎣ m + (1 / 2) M ⎦
⎡
⎤
2
a=⎢
9.81 m ⋅ s −2 = 4.905 m ⋅ s −2 .
⎥
⎣ 2 + (1 / 2 ) 4 ⎦
(4)
(5)
9-3) A particle of mass M moves in the x-y plane. Its coordinates as a function of time are given
by:
x (t ) = At 3 ; y (t ) = Bt 2 − Ct ,
where A, B and C are constants of the motion. Do the following:
a)
Calculate the angular momentum of the point particle with respect to the origin of the
coordinate system in which the position is defined.
b)
Calculate the net force that acts on the particle.
By definition, the angular momentum
mass is given by
  of a movingpoint

L=r × p=M r×v .
(1)
As the motion of the point mass is restricted to the x-y plane, the angular momentum--cross
product--is perpendicular to the plane, and, therefore, parallel to the z-axis. So, we can rewrite
equation (1) as
[
]

⎡ dry
dr ⎤
L = M ⎡⎣ rxv y − ryv x ⎤⎦ k̂ = M ⎢ rx
− ry x ⎥ k̂
dt ⎦
⎣ dt
= M ⎡⎣ At 3 ( 2Bt − C ) − Bt 2 − Ct 3At 2 ⎤⎦ k̂
( )
(
)(
)
= M ⎡⎣ 2ABt 4 − ACt 3 − 3ABt 4 + 3ACt 3 ⎤⎦ k̂
= M ⎡⎣ 2ACt 3 − ABt 4 ⎤⎦ k̂ = MAt 3 ( 2C − Bt ) k̂ .
(2)
The net force is, by definition, the time rate of change of the linear momentum. So, we have
 dp
d
2
F=
= M ⎡⎣ 3At î + (2Bt − C ) ĵ ⎤⎦ = M ⎡⎣ 6At î + 2B ˆj ⎤⎦ .
dt
dt
(
)
(3)
9-4) A cyclist is turning to the left as she moves at constant speed v on a circular path of radius r .
Assume that the rear wheel of radius R and moment of inertial I remains vertical. Do the
following:
a)
Draw a careful diagram of the path of the motion of the rear wheel, include an
appropriate coordinate system. Also, draw two angular momentum vectors at two times
S 9-3
b)
c)
separated by short interval.
In the coordinate system you have defined, identify the direction of the angular
momentum.
Calculate the time rate of change of the angular momentum and show that
dL / dt = 2K ,
where K is the rotational kinetic energy.
9-5) A solid sphere of mass m and radius a moves without rolling over a level, frictionless
surface with speed vo when it encounters a rough patch for which the coefficient of friction µ .
Do the following:
a)
Show that rolling without slipping begins when the speed of the center of mass is
5vo / 7 .
b)
Calculate the distance the center of mass moves before the sphere rolls without slipping.
N


vo
a
m
smooth
rough
mg
f = µ mg
a) The friction will provide a torque on the sphere that will change its angular momentum for
zero to the value it has when it stops slipping and begins to roll without slipping; when the kinetic
friction is transformed to static friction. Summing forces perpendicular to the motion gives us
N − mg = mavertical = 0 → N = mg → f = µ mg .
(1)
Summing the forces parallel to the motion we find
− µ mg = maparallel → a parallel = − µ g .
(2)
As the friction force is constant, then its average and instantaneous values are the same and we
can write
Γ = Γ ave = R µ mg =
and
ΔL Iω − 0 1 ⎡ 2
2⎤ ⎡ v ⎤
=
= ⎢ mR ⎥ ⎢ ⎥ ,
Δt
t −0
t ⎣5
⎦ ⎣ R⎦
5
v = µ gt .
2
As long as there is acceleration due to kinetic friction, then we can write
v = vo − µgt → µ gt = vo − v .
Using equation (5) in equation (4) results in
v=
b)
5
2
5
7
5
(vo − v ) → v = v o − v → v = v° → v = vo .
2
5
5
5
7
(3)
(4)
(5)
(6)
For constant acceleration
1 ⎤
⎡
Δr = t ⎢ vo + at ⎥ .
2 ⎦
⎣
S 9-4
(7)
Using equation (5) we can write
µgt = vo −
5
2
2 vo
vo = vo → t =
.
7
7
7 µg
(8)
Using the results of equations (2) and (8) is (7) leads to
⎛ 2 vo ⎞ ⎡
1
⎛ 2 v o ⎞ ⎤ ⎛ 2 vo ⎞ ⎡
1 ⎤
(
)
Δr = ⎜
v
+
−
µ
g
=
v
−
v
⎢
o
⎥
o
⎜⎝ 7 µ g ⎟⎠
⎜
⎟⎢
⎝ 7 µg ⎟⎠ ⎣
2
7 o ⎥⎦
⎦ ⎝ 7 µg⎠ ⎣
⎛ 2 vo ⎞ ⎡ 6 ⎤ 12 vo2
=⎜
v =
.
⎝ 7 µg ⎟⎠ ⎢⎣ 7 o ⎥⎦ 49 µ g
(9)
9-6)
N
m

F


F
r
R
rough
mg
fs = µ s N
A spool of radius R and mass m with an axle of radius r is represented in the diagram
above. A light string is wrapped around the axle and a tensile force F is applied to the spool and
results in the spool rolling without slipping. The moment of inertia about the axis of rotation is
2
given by (1 / 2 ) mR . Do the following:
a)
Calculate the magnitude of the acceleration of the center of mass.
b)
Calculate the magnitude of the friction.
a)&b) Summing vertical forces,
N − mg = mavertical = 0 → N = mg → fs = µs mg .
(1)
Summing horizontal forces,
F − µs mg = ma → F = µ s mg + ma .
(2)
Summing torques about the center we have
1
⎡1
2 ⎤⎛ a⎞
r ( µ s mg + ma ) + R ( µs mg ) = Iα = ⎢ mR ⎥ ⎜ ⎟ = mRa .
⎣2
⎦⎝ R⎠ 2
(3)
⎡ r+R ⎤
2 µ s g ( r + R ) = ( R − 2r ) a → a = 2 µs ⎢
⎥g .
⎣ R − 2r ⎦
(4)
Equation (3) implies
S 9-5
9-7)
N
m

r
T
mg
R
f = µN
T
rough
A spool of radius R and mass m with an axle of radius r is represented in the diagram
above. A light string is wrapped around the axle and a tensile force T is applied to the spool and
results in the spool rolling without slipping. The moment of inertia about the axis of rotation is
2
given by (1 / 2 ) mR . Show that the tension needed to roll without slipping is given by
T=
a)&b) Summing vertical forces,
3µ mgR
.
R + 2r
N − mg = mavertical = 0 → N = mg → f = µ mg .
Summing horizontal forces,
µmg − T = ma → T = µ mg − ma .
(1)
(2)
Summing torques about the center we have
1
⎡1
2 ⎤⎛ a ⎞
r ( µ mg − ma ) − R (µmg ) = I α = ⎢ mR ⎥ ⎜ ⎟ = mRa .
⎣2
⎦⎝ R ⎠ 2
(3)
Equation (3) implies
⎡ R−r ⎤
−2 µ g ( R − r ) = ( R + 2r ) a → a = −2 µ g ⎢
⎥.
⎣ R + 2r ⎦
(4)
Equation (4) into equation (2) yields
⎡
⎡ R− r ⎤
⎛ R− r ⎞⎤
T = µ mg + 2 µmg ⎢
=
µ
mg
1
+
2
⎜⎝
⎟
⎢
⎥
R + 2r ⎠ ⎥⎦
⎣ R + 2r ⎦
⎣
⎡ R + 2r + 2R − 2r ⎤
⎛ R ⎞
= µ mg ⎢
=
3
µ
⎜⎝
⎟ mg .
⎥
R + 2r
R + 2r ⎠
⎣
⎦
(5)
9-8) A lawn roller of mass m and radius R is pulled by a horizontal force F that is applied at the
center of the roller by a horizontal handle, as represented in the diagram below. Show that the
minimum coefficient of friction needed to prevent slipping is given by
µs = F / ( 3mg ) .
S 9-6
N
m
F
F
R
mg
rough
fs = µ s N
The minimum coefficient to prevent slipping means that motion is impending and the static
friction is at a maximum. So, summing vertical forces gives us
N − mg = mavertical = 0 → N = mg → fs = µs mg .
(1)
Summing horizontal forces we have
F − µs mg = ma → F − ma = µ s mg → F / m − µs g = a .
(2)
Summing torques about the center yields
R µ s mg = I α = (1 / 2 ) mR2 ( a / R ) = (1 / 2 ) mRa → µs = (1 / 2 ) a / g . (3)
Substitution of the results of equation (2) into equation (3) gives us
(
)
µs =
Therefore,
1a
1 ⎡F
F
⎤
=
−
µ
g
→ 2
µ
g
+
µ
g
=
.
s
s
s
⎥
2 g 2g ⎢⎣ m
m
⎦
µs =
F
.
3mg
(4)
(5)
9-9)

m
restraint
A uniformly thin rod of mass m and length  is pivoted at one end by a frictionless pin and
held horizontally by a restraint, as represented in the diagram above. Calculate the force exerted on
the pin at the instant the restraint is removed.
9-10) The distance between the front and back axles of a car of mass 1,200 kg is 3 m . On a
horizontal surface, the front tires carry 60% of the weight. The center of mass is 80 cm above
the road. Calculate the magnitude of the normal forces exerted on the front and the rear tires if the
car is parked on a 20° incline.
When the car is on the level, the sum of the forces and the sum of the torques must vanish.
S 9-7
mg sinθ
fR
h
NR
mg
θ
NF

NF
fF
NR θ
mg cos θ
mg
x
We are given information that allows us to write
N F = (0.6 ) mg ; N R = (0.4 ) mg → N F + N R = mg ,
(1)
as required by static equilibrium. The torques about the center of mass must vanish and, therefore,
the magnitude of the clockwise torques must equal the counter-clockwise torques. So,
( − x ) (0.4 mg ) = x ( 0.6 mg) → 0.4mg − 0.4mgx = 0.6mgx ,
(2)
and, therefore,
0.4 mg = mgx → x = 0.4 = 0.4 ( 3 m ) = 1.2 m ,
(3)
as we might have guessed.
If we sum the torques about the point of contact in the front , we have
mg
( x cosθ + h sinθ ) ,

(4)
((1.2) cos 20° + ( 0.8) sin 20°) N = 5, 498 N .
(5)
N R = xmg cosθ + hmg sin θ → N R =
Therefore,
NR =
(1200) (9.81)
3
In a similar fashion, we sum the torques about the rear point of contact. We have
N F + hmg sin θ = (  − x ) mg cos θ = → N F =
Therefore,
NF =
(1200 )(9.81)
3
mg
(( − x ) cosθ − h sin θ ) . (6)

(( 3 −1.2 ) cos20° − (0.8) sin 20°) N = 5, 564 N .
(7)
9-11) An aluminum stepladder, of negligible mass, has legs of length 4 m . The legs pivot freely
at the top and are connected at the midpoint by a segment of rope. The surface on which the ladder
is placed is level and smooth. Do the following:
a)
Calculate the tension in the rope if a person of mass 70 kg sits on top of the ladder.
b)
Calculate the tension in the rope if a person of mass 70 kg stands on the ladder at a
point a distance of 1 m along the ladder measured from the top. (See the diagram
below.)
S 9-8
T
P
θ
m
x
mg
mg − N R
/ 2
r⊥T
4m
mg
θ
T
θ
θ
θ
P′
NL

3m
r⊥ NR
NR
2cos θ
NR
Using the free-body diagram of the ladder as a whole, (see above left), summing the vertical
forces we have
↑ = ↓
N L + N R = mg .
(1)
 = 
2cos θ N R = (  cosθ + x cosθ ) mg ,
(2)
Summing the torques about point P ′ , we have
and
NR =
1⎛
⎜1 +
2⎝
x⎞
⎟ mg
⎠
(3)
Using the free-body diagram on the right leg of the ladder, (see above right), and summing
torques about point P , we have:
 = 
⎛1⎛
⎜1 +
⎝2⎝
( x cosθ ) mg + (( / 2 ) sin θ ) T = (  cosθ ) ⎜
and
Therefore,
1
⎛ 1⎛
T tan θ = ⎜ ⎜ 1 +
2
⎝ 2⎝
x⎞ ⎞
x
⎛⎛
⎟⎠ mg⎟ − mg → T = ⎜ ⎜⎝ 1 +

⎠

⎝
T = (1− ( x / )) mg / tan θ .
S 9-9
x⎞ ⎞
⎟ mg ,
 ⎠ ⎟⎠
(4)
x⎞
x ⎞ mg
. (5)
⎟⎠ − 2 ⎟

 ⎠ tanθ
(6)
a)
b)
When the person is sitting in the middle, x = 0 , and equation (6) becomes
(
)
−2
mg ( 70 kg ) 9.81 m ⋅ s
T ( x = 0) =
=
= 278 N .
tan θ
tan cos−1 (1.5 / 4 )
(
When x = 1 , we have
T ( x = 1) =
)
(7)
3 mg
= 208 N .
4 tan θ
(8)
9-12)
NW
M
mg

m
Mg
x
θ
θ
µs N f
Nf
A ladder of mass M and length  rests against a smooth, vertical wall at an angle θ to the
horizontal, as represented in the diagram above. The floor on which the ladder sits is rough and the
coefficient of friction is µ . A person of mass m stands vertically on the ladder at a point a
distance x measured from the bottom, as represented in the diagram above. There is a value of x
at which the ladder will begin to slip. Do the following:
a)
Derive expressions, in terms of the parameters given, for the horizontal and vertical
forces exerted on the ladder by the floor and the wall when motion is impending.
b)
Quantify the values of interest if:
 = 3 m , M = 10 kg , m = 50 kg , θ = 70°, x = 1 m , µ = 0.131 .
a) As the wall is frictionless, it can only exert a normal force. Also, as motion is impending, the
static frictional force is at a maximum and equal µs N f .
Summing horizontal forces, we have
→ = ←
NW = µ s N f .
S 9-10
(1)
Summing the vertical forces, we find
and, therefore,
b)
↑ = ↓
N f = (m + M ) g ,
(2)
NW = µ s ( m + M ) g .
(3)
For the values given:
(
)
N W = ( 0.131)( 50 kg + 10 kg) 9.81 m ⋅ s −2 = 77.1 N = fs ,
(
)
N f = (50 kg + 10 kg ) 9.81 m ⋅ s −2 = 589 N = fs .
and
(4)
(5)
9-13) A turntable with a moment of inertia of 0.012 kg ⋅ m rotates with a constant angular
speed of 2 rad / s . A circular disk of mass 200 grams and diameter of 30 cm , and initially
not rotating, slips down a spindle and lands on the turntable. Do the following:
a)
Calculate the angular speed of the disk and turntable after the collision.
b)
Calculate the change in the rotational kinetic energy of the “system.”
2
a) During the completely inelastic collision between the turntable and the disk, there is no net
torque. Therefore, the angular momentum is conserved and we can write:
Ioω o = I f ω f ,
(1)
and
ωf =
where
Io
IT
−1
ωo =
ωo = (1 + a ) ω o ,
If
IT + I D
(2)
ID (1 / 2 ) mD RD2 (1 / 2) (0.20 kg )( 0.15 m )
3
a=
=
=
= 0.1875 =
. (3)
2
IT
IT
0.012 kg ⋅ m
16
2
With regard to the kinetic energy, the change is defined by
2
1
1
−1
2
IT (1+ a ) ⎡⎣ (1 + a ) ω o ⎤⎦ − IT ω o
2
2
⎡
(1 + a ) ⎤ 1 2 ⎡
1
1 ⎤
2
= − IT ω o ⎢1 −
IT ω o ⎢1−
2 ⎥ = −
⎥ .
2
2
⎣ 1+ a⎦
⎢⎣ (1 + a ) ⎥⎦
ΔKrot = K rot, f − K rot,i =
a)
Using equations (2) and (3), we have
ω f = (1 + a) ω o = (1 + ( 3 / 16 ))
−1
b)
−1
( 2 rad / s ) = 1.68 rad / s .
(4)
(5)
Using equations (4) and (3), we find
1
1 ⎤
1
1 ⎤
2 ⎡
2 ⎡
2
= − IT ω o ⎢1 −
=
−
0.012 kg
⋅
m
2 rad
/
s
1−
(
)
⎥
⎢ 19 / 16 ⎥
2
2
⎣ 1+ a⎦
⎣
⎦
= −0.0039 J .
(
)
(6)
So, in a completely inelastic collision of a system involving rotation, the angular momentum is
conserved and kinetic energy is “lost”. We have found general relationships given by
−1
−1
ω f = (1 + a) ω o and ΔKrot = −K rot ,o ⎡⎣1 − (1+ a ) ⎤⎦ ,
S 9-11
(7)
where
a = I added / Io .
(8)
9-14)
60 kg

v
3m
100 kg
A person of mass 60 kg runs with a velocity 5 m / s along a tangent to a stationary to a
stationary circular platform of radius 3 m and mass 100 kg and jumps onto it. The platform is
free to rotate about a fixed vertical axis, as represented in the diagram above. Do the following:
a)
Calculate the angular speed of the platform just after the person lands on it.
b)
Calculate the change in rotational kinetic energy.
a) We have another completely inelastic collision involving rotation. So, we use the results of
the preceding problem. We note that
We also note that
1
M
2
2
2
Io = mr⊥ = mR and MR → a =
.
2
2m
(1)
ωo = v / R .
(2)
Therefore,
ω f = (1 + a)
b)
−1
−1
−1
M ⎞ ⎛ v⎞ ⎛
100 kg ⎞ ⎛ 5 m / s ⎞
⎛
ω o = ⎜1 +
=
1+
⎝
2m ⎟⎠ ⎜⎝ R ⎟⎠ ⎜⎝
2 (60 kg ) ⎟⎠ ⎜⎝ 3 m ⎟⎠
= 0.909 rad / s .
For the change in rotational kinetic energy, we have
−1
2 ⎡
⎛
1
1
100 ⎞ ⎤
−1
2
2 ⎛ v⎞
⎥
ΔKrot = − Ioω o ⎡⎣1 − (1+ a ) ⎤⎦ = − mR ⎜ ⎟ ⎢1 − ⎜ 1 +
⎝ R⎠ ⎢ ⎝
2
2
2 (60 ) ⎟⎠ ⎥
⎣
⎦
1 2
1
2
= − mv [ 5 / 11] = − ( 60 kg )(5 m / s ) [ 5 / 11] = −341 J .
2
2
(
(3)
)
(4)
9-15) A uniform rigid solid rotates freely about a fixed axis with a period τ . If its moment of
inertia changes by an infinitesimal amount dI . Do the following:
dI dτ
=
.
I
τ
a)
Show that
b)
The Saudi Arabian government at one time considered the feasibility of towing
icebergs from the Antarctic to supplement their water supply. Estimate how the length
S 9-12
13
of a day would be changed if 10 kg of ice were moved from the pole to the
2
equator without melting. Treat the moment of inertia of the Earth as 0.33M ⊕ R⊕ .
a)
and
We know the angular momentum of a rotating solid about a fixed axis is given by
L = Iω ,
dL d
dI
dω
= [ Iω ] = ω + I
.
dt dt
dt
dt
(1)
(2)
The angular momentum would be conserved in an infinitesimal change in the moment of inertia.
Thus, leading to
0=
dI
dω
dI
dω
dI
dω
ω +I
→ ω = −I
→ = −
.
dt
dt
dt
dt
I
ω
For a periodic angular speed, we can write
(
dω = d 2πτ
−1
)
(
)
−2π / τ 2 dτ
2π
dω
dτ
= − 2 dτ → =
=−
.
τ
ω
2πτ
τ
(3)
(4)
Therefore, we can rewrite equation (3) as
b)
dI
dω
⎡ dτ ⎤ dτ
=−
= − ⎢− ⎥ =
.
I
ω
⎣ τ ⎦ τ
(5)
Integrating the results of equation (15) gives us
I
∫
Io
τ
dI
dτ
⎡I ⎤
⎡τ ⎤
I
τ
= ∫ − → ln ⎢ ⎥ = ln ⎢ ⎥ → =
.
I τ τ
I
τ
I
τ
⎣ o⎦
⎣ o⎦
o
o
(6)
o
So,
I
⎡ mR⊕2 + 0.33M ⊕ R⊕2 ⎤
⎡ m + 33M ⊕ ⎤
⎡
m ⎤
τ = τo = ⎢
⎥τ o = ⎢
⎥ τ o = ⎢1 +
⎥τ o .
2
Io
0.33M
R
0.33M
0.33M
⎣
⊕ ⊕
⎦
⎣
⊕ ⎦
⎣
⊕ ⎦
(7)
Note that
⎡
m ⎤
⎡
m
⎤
⎡ m ⎤
Δτ = τ − τ o = ⎢1+
−1⎥ τ o = ⎢
⎥ τ o − τ o = ⎢1 +
⎥τ o
0.33M
0.33M
0.33M
⎣
⊕ ⎦
⎣
⊕
⎦
⎣
⊕ ⎦
⎡
⎤
1013 kg
=⎢
⎥ (24 ( 3,600 s )) = 4.40 × 10−7 s .
(8)
24
⎢⎣ 0.33 5.97 ×10 kg ⎥⎦
−7
The rotation of the Earth would slow such that every day would require 4.40 × 10 s more
−4
time to complete one rotation. Over a year that would result in 1.6 × 10 s more time needed to
(
)
complete one orbit of the Sun. (The “longer” time is equivalent to a “loss” in time.)
9-16) A thin ring of mass M and radius R spins about a vertical diameter, as represented in the
2
diagram below. Take its moment of inertia as (1 / 2 ) MR . A small bead of mass m can slide
without friction along the ring. When the bead was at the top of the ring, the angular spin was ω o .
Do the following:
S 9-13
a)
b)
Use the conservation of angular momentum to derive an equation for the angular speed
ω in terms of the angle ϕ , measured from the vertical.
For the following values, M = 1.00 kg , R = 0.400 m , m = 0.2 kg ,
ω o = 5 rad / s and ϕ = 45° .
r̂
ω
R sin ϕ
rˆ ′
m
ϕ
R
M
a)
and
b)
The conservation of angular momentum gives us
1
⎛1
2⎞
2
2
Ioω o = I Lω → MR ω o = ⎜ MR + m ( R sin ϕ ) ⎟ ω .
⎝2
⎠
2
(1)
⎡
M
⎤
M ωo = M + 2m sin 2 ϕ ω → ω = ⎢
2
⎥ω o .
⎣ M + 2m sin ϕ ⎦
(2)
⎡
⎤
1 kg
ω =⎢
⎥ (5 rad / s ) = 4.17 rad / s .
2
⎣ 1 kg + 2 ( 0.20 kg ) sin 45° ⎦
(3)
(
)
For the values given, we have
9-17)

v
R
m
M
M
A particle of mass m travels on a horizontal circular path on top of a frictionless table, as
represented in the diagram above. The radial force is provided by a light string, attached to two
S 9-14
bodies of equal masses, which passes through a hole in the table. Use the conservation of angular
momentum to show that if the bottom mass is removed, the radius of the motion changes by a factor
of 1.26 .
The tension in the string initially, is given by
To = 2Mg → 2Mg = mRo ωo → ω o =
2
2Mg
.
mRo
(1)
Later, the radius is given by R = nRo and
T = Mg → Mg = m (nRo ) ω → ω =
2
Mg
,
mnR o
(2)
Recall that the moment of inertia of a point mass is given by I = mr⊥ . The conservation of
angular momentum requires
2
Ioω o = Iω → mRo
2
2Mg
Mg
2 2
= mn Ro
.
mRo
mnRo
(3)
Squaring both sides, we find
2
4
m Ro
Therefore,
while
2Mg
4 4 Mg
3
1/ 3
= mn Ro
→ n = 2 → n = 2 = 1.260 .
mRo
mnRo
ΔR = R − Ro = nRo − Ro = Ro ( n −1) = 0.260Ro ,
R
= n = 1.260 .
Ro
(4)
(5)
(6)
9-18)
ĵ
JAC
M
m

m

u
JBC
M
M
cm

v
M
m
cm
cm calculation
M
î

r⊥

M
A particle of mass m = 0.500 kg moving at speed u = 4 m / s strikes a dumbbell
consisting of equal mass M = 1 kg separated by a massless rod of length 2 m , as represented in
in a top view in the diagram above. The particle and dumbbell are free to slide on a horizontal,
frictionless surface. Do the following:
a)
Calculate the speed of the center of mass just after the particle sticks to the mass with
which it collided.
b)
Calculate the angular speed of system with respect to the center of mass.
a) Using the conservation of linear momentum, we have
mu = ( m + 2 M ) v ,
(1)
S 9-15
and
⎡ 0.50 kg ⎤
⎡ m ⎤
v=⎢
u
=
⎢ 0.50 kg + 2kg ⎥ ( 4 m / s ) = 0.80 m / s .
⎣ m + 2M ⎥⎦
⎣
⎦
(2)
2
⎡⎣ mr⊥2 ⎤⎦ (v / r⊥ ) = ⎡ mr⊥2 + Mr⊥2 + M ( − r⊥ ) ⎤ ω ,
⎣
⎦
(4)
b) Using the conservation of angular momentum, and treating all masses as point masses, we
have
Ioω o = Iω .
(3)
and
while
2
⎡
( − r⊥ ) ⎤
[ m ]( v / r⊥ ) = ⎢ m + M + M r2 ⎥ ω .
⎢⎣
⎥⎦
⊥
(5)
The value of r⊥ is, of course the magnitude of the center of mass measured from the top mass of the
dumbbell. We can calculate this by using
1 N
1


rcm,y =
mi ry,i =
⎡⎣ m ( 0 ) + M (0 ) + M ( − )⎤⎦ ĵ
∑
M tot i=1
m + 2M
M
1
4
4
=−
 ˆj = −
(2 m ) ĵ = − ĵ → rcm,y = m .
m + 2M
5
5
(1 / 2 ) + 2
( − r⊥ )
2
So,
((10 / 5 ) − 4 / 5)
=
2
( 4 / 5 )2
r⊥2
(6)
= 2.25 .
(7)
Using the values found in (7) and (6) in equation (5) gives us
ω=
(5 / 4 ) mv
m + 3.25 M
=
2
(5 / 4 )(1 / 2 )( 4 )
rad / s = rad / s .
3
(1 / 2 ) + 3.25 (1)
(8)
9-19)
θ
T
mg
m
Mg
M
PH
θ
30°
PV
S 9-16
A 20 kg boom of length 4 m is attached to a vertical wall by means of a pivot. A
supporting cable is attached at a right angle to the boom at a point 3 m along the boom measured
from the pivot, as represented in the diagram above. The supporting cable has a breaking tension of
1000 N . A mass m hangs from the end of the boom. The system is in static equilibrium. Do
the following:
a)
Calculate the maximum value of m that can be hung from the boom without breaking
the supporting cable.
b)
Calculate the horizontal and vertical forces exerted on the boom by the pivot pin in this
case.
a) To calculate the maximum value of the hanging mass, we sum the torques about the pivot.
Equilibrium requires
 = 
⎡⎣( / 2 ) cosθ ⎤⎦ Mg + [ cos θ ] mmax g = ⎡⎣( 3 / 4 )  ⎤⎦ Tmax ,
(1)
and
mmax =
3 Tmax
M ⎡3
1,000
20 ⎤
−
=⎢
− ⎥ kg = 78.28 kg . (2)
4 g cosθ 2 ⎣ 4 ( 9.81) cos 30° 2 ⎦
To find PH , we use the requirement of static equilibrium that
b)
→ = ←
PH = Tmax sin θ = (1000 N ) sin 30° = 500 N .
(3)
The conditions of static equilibrium, with regard to vertical forces, requires
PV + Tmax
and, therefore,
↑ = ↓
cosθ = ( M + mmax ) g → PV = ( M + mmax ) g − Tmax cosθ ,
PV = ⎡⎣( 20 + 78.28 ) (9.81) − (1, 000) cos 30°⎤⎦ N = 98 N .
(4)
(5)
9-20)
θ

T

m
m
θ
PH
θ
mg
mg
PV
One end of a strut of mass m and length  is free to rotate about a horizontal pin of a hinge
assembly. The other end of the strut is attached to a light cable which, in turn, is fixed to a vertical
wall, as represented in the diagram above. A second cable is attached to the strut and holds up a
load, also of mass m . The strut is angled θ = 30° to the horizontal. The system is in static
S 9-17
equilibrium. In terms of mg , do the following:
a)
Calculate the tension in the cable attached to the load.
b)
Calculate the tension in cable attached to the vertical wall.
c)
Calculate the magnitude and direction, with respect to the horizontal, of the force exerted
on the strut by the pin.
a)
b)
As the load is at rest, the tension in the cable must equal the weight of the load. So,
Tload = mg .
Summing torques about the pivot, static equilibrium constraints give us
⎡⎣( / 2 ) cosθ ⎤⎦ mg + [  cosθ ] mg = ( sinθ ) T → T =
Therefore,
T=
c)
3 mg
.
2 tan θ
3 mg
3 3
=
mg = 2.60mg .
2 tan 30° 2 3
Summing vertical forces,
PV = 2mg ,
(1)
(2)
(3)
(4)
while summing horizontal forces, we find
PH = T =
9
2 3
mg .
(5)
Therefore, the magnitude of the force exerted on the strut by the pin is given by
2
81
129
43
⎛ 9 ⎞
P = 2 + ⎜
mg = 4 + mg =
mg =
mg = 3.28 mg .
⎟
⎝ 2 3⎠
12
12
2
2
(6)
The angle the pin force makes to the horizontal is given by
⎡
⎤
⎢ 2mg ⎥
⎡P ⎤
−1 ⎡ 4 tan 30° ⎤
θ ′ = tan−1 ⎢ V ⎥ = tan −1 ⎢
= tan ⎢
⎥
⎥ = 37.6° .
3
mg
P
3
⎣
⎦
⎣ H⎦
⎢
⎥
⎣ 2 tan 30° ⎦
(7)
9-21)
One end of a strut of mass m and length  is free to rotate about a horizontal pin of a
hinge assembly. The other end of the strut is attached to a light cable which, in turn, is fixed to a
horizontal surface as represented in the diagram below. A second cable is attached to the strut and
holds up a load, also of mass m . The strut is angled θ = 45° to the horizontal, while the cable
attaching the strut to the horizontal surface is angled ϕ = 30° to the horizontal. The system is in
static equilibrium. In terms of the parameters given, do the following:
a)
Calculate the tension in the cable attached to the load.
b)
Calculate the tension in cable attached to the horizontal surface.
c)
Calculate the magnitude and direction, with respect to the horizontal, of the force exerted
on the strut by the pin.
a) The load is at rest, so the tension holding up the load is equal to its weight, that is,
Tload = mg .
(1)
b) To calculate the tension in the other cable, we sum the torques about the pin. Static
equilibrium requires the magnitudes of the clockwise and counter-clockwise torques to be equal.
So,
S 9-18
⎡⎣( / 2 ) cosθ ⎤⎦ mg + [  cosθ ] mg = ( sin (θ − ϕ )) T → T =
and
T=
3 mg cosθ
,
2 sin (θ − ϕ )
3 mgcos θ
3cos 45°
=
mg = 4.098 mg .
2 sin (θ − ϕ ) 2 sin (45° − 30°)
T cos ϕ
ϕ
T
T sin ϕ
m
c)
−

m
θ = 45°
ϕ = 30°
θ
PH
m
(3)
mg
ϕ

r⊥
(2)
mg
θ
PV
The magnitude of the force exerted on the strut by the pin is given by
P = PH2 + PV2 .
(4)
The horizontal component of the pin force is given by
PH = T cos ϕ = (4.098 mg )( cos 30°) = 3.549 mg .
(5)
The vertical component of the pin force is given by
PV = 2mg + T sin ϕ = ⎡⎣ 2 + ( 4.098 sin 30°) ⎤⎦ mg = 4.049 mg .
(6)
Using the values found in equations (5) and (6) in equation (4) yields
P = mg
(3.549 )2 + ( 4.049)2
= 5.384 mg .
(7)
The value of θ ′ , the angle the pin force makes to the horizontal, is given by
⎡P ⎤
⎡ 4.049 ⎤
θ ′ = tan−1 ⎢ V ⎥ = tan −1 ⎢
⎥ = 48.8° .
⎣ 3.549 ⎦
⎣ PH ⎦
(8)
Note that the pin force is not along the strut. There action of the forces produces a so-called
bending moment.
9-22) A uniform solid sphere of mass 0.250 kg and radius 0.125 m is released from rest at
the top of a rough plane inclined 37° to the horizontal, as represented in the diagram below. The
solid sphere rolls without slipping. Do the following:
a)
Using Newton’s second law for translational and rotational motion, calculate the
the magnitude of the acceleration of the center of the sphere relative to the incline.
b)
Calculate the speed of the center of the sphere relative to the incline at the instant it is
S 9-19
c)
at the bottom of the incline.
If we assume the static friction is given by
f = µN ,
calculate the value of µ .
m

3.6109 m
N
h =  sin θ
f
mg
37°

v
R
θ
mg cos θ
mg sinθ
θ
a) The solid sphere is both translating and rotating. To analyze the translational motion, we sum
forces parallel to the incline and find
mg sinθ − f = ma .
(1)
To analyze the rotational motion, we sum the torques with respect to the center of the solid sphere.
We get
2
2
⎡2
2 ⎤⎛ a ⎞
Rf = Iα = ⎢ mR ⎥ ⎜ ⎟ = mRa → f = ma .
5
⎣5
⎦⎝ R⎠ 5
(2)
mg sinθ = ma + f = ma + (2 / 5 ) ma = (7 / 5 ) ma ,
(3)
Substitution of equation (2) into a rearranged equation (1) yields
and, therefore,
(
)
a = ( 5 / 7) g sin θ = (5 / 7 ) 9.81 m ⋅ s −2 sin 37° = 4.217 m / s 2 .
b)
c)
(4)
As the acceleration is constant and the initial speed is zero, we can write
v = 2a = 2ah / sinθ = 2 ( 4.217 )( 3.6109 ) / sin 37° = 7.114 m / s .
If the static friction can be written as µ N , then we can write
2
2 ⎛ 5⎞
f = µ N = µ mg cosθ = ma = m ⎜ ⎟ g sinθ .
5
5 ⎝ 7⎠
(5)
(6)
Therefore,
µ=
2
tanθ = 0.215 .
7
(7)
9-23) A solid sphere of mass 0.250 kg and radius 0.125 m is moving with speed vo when it
begins rolling without slipping up a rough plane inclined 37° to the horizontal, as represented in
S 9-20
the diagram below. Do the following:
a)
Using Newton’s second law for translational and rotational motion, calculate the
the magnitude of the acceleration of the center of the sphere relative to the incline.
b)
Calculate the initial speed of the center of the sphere relative to the incline if the center
of the sphere moves 6.00 m before coming to instantaneous rest.
c)
If we assume the static friction is given by
f = µN ,
calculate the value of µ .
m

3.6109 m

vo
N
f
θ

vo
mg
R
h =  sin θ
mg cos θ
mg sinθ
θ
37°
a) The solid sphere is both translating and rotating. To analyze the translational motion, we sum
forces parallel to the incline and find
−mg sin θ − f = ma .
(1)
To analyze the rotational motion, we sum the torques with respect to the center of the solid sphere.
We get
2
2
⎡2
2 ⎤⎛ a ⎞
Rf = Iα = ⎢ mR ⎥ ⎜ ⎟ = mRa → f = ma .
5
⎣5
⎦⎝ R⎠ 5
(2)
−mg sin θ = ma + f = ma + (2 / 5 ) ma = ( 7 / 5 ) ma ,
(3)
Substitution of equation (2) into a rearranged equation (1) yields
and, therefore,
(
)
a = − ( 5 / 7 ) g sinθ = − ( 5 / 7) 9.81 m ⋅ s −2 sin 37° = −4.217 m / s 2 .
b)
c)
(4)
As the acceleration is constant and the final speed is zero, we can write
vo = 2a = 2ah / sin θ = 2 ( 4.217 )( 3.6109 ) / sin 37° = 7.114 m / s .
If the static friction can be written as µ N , then we can write
2
2 ⎛ 5⎞
f = µ N = µ mg cosθ = ma = m ⎜ ⎟ g sinθ .
5
5 ⎝ 7⎠
(5)
(6)
Therefore,
µ=
2
tanθ = 0.215 .
7
S 9-21
(7)
Solutions to Problems for Chapter Ten
10-1) A 2 kg block is pulled 3 m along a frictionless horizontal plane by a 10 N force that is
directed 37° above the horizontal , as represented in the diagram below.

F

F
N
37°
θ
m

Δr
mg
Do the following:
a)
Calculate the work done by this force.

b)
Calculate the speed of the block at the end of the 3 m , if vo = 0 .
(A free-body diagram is always advised in doing such problems.)
A general approach, in the absence of internal energies, will exploit:
N
∑W
i
= W1 + W2 + + Wi + + WN = Wtot = ΔK = K o − K L .
(1)
i=1
This is the approach I will most often use.
a) From the free body diagram we can write
WG + WN + WF = K L − K o .
(2)
As both the normal force and the gravitational forces are everywhere perpendicular the displacement
of the block, they do no work;
WG = WN = 0 .
(3)
Also, as the initial velocity is zero, then
Ko = 0 ,
(4)
and equation (2) reduces to
WF = K L = (1 / 2 ) mv 2 .
(5)

As the force F is constant, we
 know the work done by a constant force is given by

WF = F • Δr = F cos ∠between = F cos θ
= (10 N ) (3 m )(cos 37°) = 24 J .
b)
(4)
Equations (5) and (6) combine to give us
v=
2WF
=
m
2 (24 J )
= 4.9 m / s .
2 kg
(
(5)
)

10-2) A 300 gram particle is moved from an initial position r1 = 2 î − ˆj + 3 k̂ m to a later

(

)
(
)
position r2 = 4 î − 3 ĵ − k̂ m under the influence of a force F = 2 î − 3 ĵ + k̂ N .
S 10-1
Do the following:
a)
Calculate the work done by this force.

b)
Calculate the speed of the block at the end of the displacement, if vo = 0 .
a) As the force is constant, we can again use the equation for the work done by a constant force
and write


WF = F • Δr
= ⎡⎣ 2 î − 3 ĵ + k̂ N ⎤⎦ • ⎡⎣ 4 î − 3 ĵ − k̂ − 2 î − ĵ + 3 k̂ ⎤⎦ m
= ⎡⎣ 2 î − 3 ĵ + k̂ N ⎤⎦ • ⎡⎣ 2 î − 2 ĵ − 4 k̂ ⎤⎦ m = ⎡⎣ (2 ) (2 ) + (−3)( −2) + (1) (−4 )⎤⎦ J
= 6 J .
(1)
(
(
)
)
(
(
)
) (
)
b) This work results in a change in kinetic energy, where the initial kinetic energy is zero.
Therefore
WF = K L − K o =
and
2WF
=
m
v=
1 2
mv ,
2
(2)
2 ( 6 J )
= 6.32 m / s .
0.30 kg
(3)
10-3)
f

Δr
F
N

Δr
f
F
mg
mg
120°
30°
A person pushes a 10 kg crate 3 m up a 30° incline with an 80 N force parallel to the
incline. The frictional force is 22 N . Calculate the following:
a)
The work done by the person.
b)
The work done by the gravitational force.
c)
The work done by the friction.
d)
The speed of the block at the end of the 3 m if the initial speed is zero.
a)
Using the free-body diagram, we can write
=0
=0


1 2
WG + WN + WF + W f = K L − K o = mv .
2
(1)
As all of the forces are constant, we can use the equation for work done by a constant force. The
work done bythe person is given by

WF = F • Δr = F cos ∠between = F cos 0° = F = ( 80 N )( 3 m ) = 240 J .
(2)
S 10-2
b)
In a similar fashion, the work
 done by the gravitational force is given by

WG = F G • Δ r = mgcos ∠between = mg cos120°
(
)
= (10 kg ) 9.81 m ⋅ s −2 ( 3 m )( cos120°) = −147 J .
c)
The work done
 by kinetic friction is given by
d)
Using equation (1),
(3)

W f = Ff • Δr = f  cos∠between = f cos 180° = − (22 N ) ( 3 m ) = −66 J .(4)
⎡2
⎤
v = ⎢ ∑W ⎥
⎣m
⎦
1/2
1/2
⎡2
⎤
= ⎢ (240 − 147 − 66) ⎥
⎣ 10
⎦
m / s = 2.32 m / s .
(5)
10-4)
F

f
N
A tool being sharpened is held against a grinding wheel of radius 4 cm with a force of
20 N directed radially inward. (See the diagram above.) The coefficient of kinetic friction is
0.40 . Calculate the work done by the wheel on the tool in 12 revolutions.
The work done by the rough surface of the wheel on the tool, is given by
(
)
W = µ N = µ N ( N rev 2π R ) = ( 0.4 ) (20 N ) 12 ( 2π ( 0.040 m )) = 24.1 J .
(1)
10-5)
F
F
N
θ
45°

Δr
mg
f
A 1.8 kg block is moved at constant speed over a level surface for which µk = 0.250 . The
block is displaced 2 m . The block is pushed by a force directed 45° below the horizontal, as
represented in the diagram above. Do the following:
a)
Calculate the work done by force F .
b)
Calculate the work done by friction.
c)
Calculate the work done by gravity.
S 10-3
As the velocity is constant, no net work is done and the accelerations are zero.
c) The work done by gravity and normal force is zero as both forces are everywhere
perpendicular to the displacement. Therefore, we have
WF + W f = 0 → WF = −W f .
Summing the vertical forces, we have
N − mg − F sin θ = mavertical = 0 ,
which implies that
N = mg + F sin θ ,
and, therefore,
f = µk mg + µ k F sin θ .
Summing the horizontal forces we have
F cos θ − f = mahorizontal = 0 → F cosθ = f .
Using equations (4) and (5), we can write
F cos θ = µ k mg + µk F sin θ .
Solving equation (6) for F we find
⎡
µk
⎤
F=⎢
⎥ mg .
cos
θ
−
µ
sin
θ
⎣
k
⎦
At last, then, the work done by constant force F is given by
=45°

 
⎡
µk
⎤
WF = F • Δr = F cos ∠between = ⎢
⎥ mg cos 45°
cos
θ
−
µ
sin
θ
⎣
k
⎦
(1)
(2)
(3)
(4)
(5)
(6)
(7)
⎡
⎤
0.25
(1.8 kg ) 9.81 m ⋅ s −2 ( 2 m )(cos 45°) = 11.8 J . (8)
=⎢
⎥
⎣ cos 45° − ( 0.25 ) sin 45° ⎦
(
)
10-6)
N

Δr
f
mg
25°
A 60 kg skier slides 200 m along a 25° slope, as represented in the diagram above. A
constant frictional force of 20 N acts on the skies. Do the following:
a)
Calculate the work done by gravity.
b)
Calculate the work done by friction.
S 10-4
Calculate the speed of the skier at the end of the 200 m , if vo = 10 m / s .
c)
Again, all the forces are constant so we can use the equation for the work done by a constant
force. Also, the normal
 iseverywhere perpendicular to the displacement so it does zero work.
a)
WG = F • Δ r = mgcos ∠between = mg cos (90° − 25° ) = mg sin 25°
(
)
= (60 kg ) 9.81 m ⋅ s −2 ( 200 m )( sin 25° ) = 49.75 kJ .
b)
The work done by kinetic
 friction is

W f = Ff • Δr = f  cos∠between = f cos 180° = − f 
= − (20 N ) (200 m ) =−4 kJ .
c)
(1)
(2)
We have
⎡ 2 2
⎤
v = ⎢ vo + ∑ W ⎥
m
⎣
⎦
1/2
=
(10 m / s )2 + ⎡⎢
2, 000
( 49.75 − 4 )⎤⎥ m / s
⎣ 60
⎦
= 40.3 m / s .
(3)
10-7)
F

Δr
mg
Calculate the work needed to lift 15 kg of water from a well 12 m deep. Assume the water
is lifted at constant speed.
We can write
WF + WG = ΔK = 0 → F = mg .
(1)
Therefore,
=0°

 
−2
WF = F • Δr = mg cos∠between = mg = (15 kg) 9.81 m ⋅ s (12 m ) = 1.77 kJ . (2)
(
)
10-8) An inclined conveyor belt is represented in the diagram below. The belt lowers a box of
mass m = 20 kg at a constant speed of v = 3 m / s . Do the following:
a)
Calculate the work done by the motor in moving the box a distance of  = 2 m .
b)
Calculate the work done by the motor in raising the box through the same distance at
the same speed.
S 10-5
20°
N

Δr

f


m
U =0
G
mg
h
θ
As the speed is constant,
Wmotor + WG = 0 → W motor = −WG .
(1)
The normal force does no work as it is everywhere perpendicular to the displacement. The static
friction does no mechanical work as it does not actually displace any physical thing. The
gravitational force can be treated as constant over such a short vertical distance and we could, as we
have done before use the work done by a constant force. However, the gravitational force is
conservative and so has an associated potential energy. We can almost always use the change in
potential energy to calculate the work done by a conservative force. So, in general, we can write
WG = U oG − U GL = mgho − mghL = −mg Δh .
(2)
a) In lowering the box,
Δh = hL − ho = 0 −  sin θ = − sin θ ,
(3)
and the work done by gravity
(
)
WG = −mg ( − sin θ ) = mg sin θ = (20 kg ) 9.81 m ⋅ s −2 ( 2 m )( sin 20°) = 134 J .(4)
Therefore, the work done by the motor would be
b)
and
In raising the box,
Wmotor = −WG = − (134 J ) = −134 J .
(5)
Δh = hL − ho =  sin θ − 0 =  sin θ ,
(6)
(
)
WG = −mg (  sinθ ) = − ( 20 kg ) 9.81 m ⋅ s−2 (2 m ) (sin 20°) = −134 J ,
(7)
while the work done by the motor would be
Wmotor = −WG = − ( −134 J ) = 134 J .
(8)
10-9) A spring has a spring constant ksp = 40 N ⋅ m . Do the following:
-1
a)
b)
Calculate the work needed to stretch the spring from equilibrium to 0.10 m .
The spring is compressed 0.10 m from equilibrium. Calculate the work needed to
compress it to 0.20 m .
Within the elastic limit, the work done by a spring is given by
Wsp = U osp −U sp
(1)
L .
As the spring cannot displace itself from a resting equilibrium position, some other physical agency
must do work. So, we can write
sp
Wother + Wsp = ΔK = 0 → Wother = −Wsp = U sp
(2)
L − Uo .
a) In stretching the spring according to the conditions given, the work done by the applied force
S 10-6
Wother =
b)
1
1
2
2
ksp ⎡⎣ x − 0 ⎤⎦ = (40 N / m ) (0.1 m ) = 0.20 J .
2
2
(3)
During the compression described, we have
Wother =
1
1
2
2
2
2
ksp ⎡⎣ x − xo ⎤⎦ = ( 40 N / m) ⎡⎣( 0.2 m ) − (0.1 m ) ⎤⎦ = 0.60 J .
2
2
(4)
10-10) Two springs have stiffness constants related by k1 > k2 . Calculate the ratio of the work
done on them, W1 / W2 , if:
a)
they are extended the distance x . 
b)
they are subjected to the same force F .
Again, we note
sp
Won +Wsp = ΔK = 0 → Won = −Wsp = U sp
L − Uo .
a) If both are extended the same distance x , then:
1
2
Wother ,1 = k1 x ,
2
1
2
Wother ,2 = k2 x ,
and
2
Wother ,1 (1 / 2 ) k1 x 2 k1
=
=
the ratio is
.
Wother ,2 (1 / 2) k2 x 2 k2

b) If they are subjected to the same force F :
F = k1 x1 = k2 x2 .
k
x1 = 2 x 2 .
and, therefore,
k1
(1)
(2)
(3)
(4)
(5)
(6)
2
So,
while
Therefore, the ratio is
1 2 1 ⎡ k2 ⎤
1 k22 2
Wother ,1 = k1 x1 = k1 ⎢ x2 ⎥ =
x ,
2
2 ⎣ k1 ⎦
2 k1 2
1
2
Wother ,2 = k2 x2 ,
2
2
2
1 k2 2 k2
x
Wother ,1 2 k1 2
k
k
=
= 1 = 2 .
1
Wother ,2
k 2 k1
k2 x22
2
10-11) Do the following:
a)
Derive an expression for the orbital kinetic energy of the Earth when the Earth is a
a distance r from the Sun.
b)
Derive an expression for the gravitational potential energy of the Earth-Sun system
S 10-7
(7)
(8)
(9)
c)
at this same point.
11 Calculate the values of interest in parts a) and b) if: r = 1.496 × 10 m .
a) If we treat the orbit as circular, then we can get average values for the quantities of interest.
We have, then.
GM  M⊕ M⊕ v2
GM  M ⊕
2
=
→ M
v
=
.
⊕
r2
r
r
Therefore,
K orb,⊕ =
b)
(1)
1
1 ⎡ GM  M ⊕ ⎤
M⊕ v2 = ⎢
⎥⎦ .
2
2⎣
r
(2)
The gravitational potential energy of the Sun-Earth system is given by
⎡ GM  M ⊕ ⎤
G
U ⊕
= −⎢
⎥⎦ .
r
⎣
(3)
Note that the magnitude of the gravitational potential energy is twice that of the kinetic energy. The
total mechanical energy of the Earth is negative and given by
1 ⎡ GM  M ⊕ ⎤
⎡ GM  M ⊕ ⎤ 1 ⎡ GM  M ⊕ ⎤
Emech ,⊕ = K + U G = − ⎢
+
=
−
⎥⎦ 2 ⎢⎣
⎥⎦
⎥⎦ . (4)
r
r
2 ⎢⎣
r
⎣
This is because the Earth is “bound”. This result is an example of what is called the virial
theorem. For the Earth to “escape” from its bound orbit, it would have to have its kinetic energy
doubled. This same phenomenon also turns out to be the case for electrons in their orbit of the
nucleus. Another consequence of this state of affairs is that when objects change their orbital
distances, the mechanical energy is not conserved.
c) A good estimate, then of the Earth’s orbital kinetic energy is found using r = a , where a is
the semi-major axis of the elliptical orbit on which the Earth moves with respect to the center of the
Sun; its average distance. We have
K orb,⊕
( 6.67 × 10
=
−11
)(
)(
N ⋅ m 2 ⋅ kg−2 1.99 × 10 30 kg 5.97 × 1024 kg
(
2 1.496 ×1011 m
)
)
= 2.65 × 1033 J .
(5)
⎡ GM  M ⊕ ⎤
G
U ⊕
= −⎢
= −5.30 ×10 33 J .
⎥
r
⎣
⎦
(6)
The gravitational potential energy, then, is
10-12) A 200 gram ball is thrown vertically upward with an initial speed 20 m / s and reaches a
maximum height of 18 m . Assume the air resistance is negligible. Do the following:
a)
Calculate the change in the kinetic energy of the ball over this interval.
b)
Calculate the work done by gravity over this same interval.
c)
Why might it be that the values in parts a) and b) are not the same?
a)
The change in the kinetic energy of the ball is given by
ΔK = K L − K o = 0 − (1 / 2 ) mvo2 = − (1 / 2 )( 0.20 kg ) (20 m / s ) = −40 J .
2
S 10-8
(1)
b)
The work done by gravity is
WG = U oG − U GL = −mgΔh = −mg (hL − ho )
(
)
= − (0.20 kg ) 9.81 m ⋅ s−2 (18 m ) = −35.3 J .
(2)
c) Maybe we really can not ignore air resistance if we want our theories to match the empirical
data. Having said that, I can only point out that air resistance is quite complicated to model
mathematically.
3
10-13) Calculate the energy needed to move a car of mass 10 kg against a constant dissipative
force of 250 N subject to the following conditions:
a)
A constant speed of 20 m / s for 10 s .
b)
A constant acceleration from rest to a speed of 20 m / s in 10 s .
c)
A constant acceleration from 20 m / s to 40 m / s in 10 s .
FD
fs
NR
mg

Δr
NF
If we look at the force diagram, we can write
=0
=0
=0



W f s +WG + WFD + WN = K L − K E .
(1)
The static friction can do no work, the gravitational force does no work over a level path, and the
normal forces do no work as they are are everywhere perpendicular to the path. Dissipative forces
will take out kinetic energy. Where, then, is the energy coming from to move the vehicle? It is
coming from internal energy; from the transformation of chemical potential energy into some useful
mechanical energy. So, we write, instead,
Wengine + WFD = K L − K E → W engine = K L − K E − WFD .
(2)
Now, as the dissipative force is constant, we can write
Wdissipative
=180°

= FD cos ∠between = −FD  .
(3)
We can now rearrange equation (2) as
a)
b)
Wengine = K L − K E − (−FD  ) = K L − K E + FD  .
Over this interval, ΔK = 0 , and
Wengine = FD  = FD (vt ) = ( 250 N )( 20 m / s )(10 s ) = 50 kJ .
Over this interval,
where
Also,
ΔK = (1 / 2 ) mv 2 ,
v − 0 20 m / s
2
a=
=
= 2 m / s .
t
10 s
S 10-9
(4)
(5)
(6)
 = (1 / 2 ) at 2 .
Therefore,
(7)
Wengine = (1 / 2 ) mv 2 − 0 + FD (1 / 2 ) a ( t ) = (1 / 2 ) ⎡⎣ mv 2 + FD at 2 ⎤⎦
2
c)
2
2
= (1 / 2) ⎡⎣(1,000 )( 20 ) + ( 250) (2 )(10 ) ⎤⎦ J = 2.25 × 10 5 J .
Over this interval,
while
Therefore,
(
(8)
)
ΔK = (1 / 2 ) m v 2 − vo2 ,
(9)
 = vot + (1 / 2 ) at 2 .
(10)
(
)
Wengine = (1 / 2 ) m v2 − v2o + FD ⎡⎣ vo t + (1 / 2 ) at 2 ⎤⎦
2
2
2
= (1 / 2) (1,000 ) ⎡⎣( 40 ) − ( 20 ) ⎤⎦ J + ( 250 ) ⎡⎣( 20 )(10 ) + (1 / 2 )( 2) (10 ) ⎤⎦ J
= 6.75 × 105 J .
(11)
10-14)
m v
A 10 gram bullet moving at 400 m / s is stopped in 2.5 cm by a wooden block of
mass 1.75 kg held firmly in place, as represented in the diagram above. Use work-energy
methods to calculate the magnitude of the average force exerted on the bullet by the block.
We know that the average force is equal to a constant force exerted over the same interval. So,
as the force is constant, we can write
=cos
180°=−1
=0





1 2  
W = K − K o = − mv = F • Δ r = ( F )( Δr ) (cos ∠bet ) = −F ( Δr ) ,
2
and, therefore,
mv 2
(0.010 )( 400 )
4
F=
=
N = 3.2 ×10 N .
2 (Δr )
2 (0.025 )
(1)
2
(2)
10-15) Use work-energy methods to do the following:
a)
Show that the minimum stopping distance for a car of mass m moving with speed vo
is given by
Δxmin
v2o
=
,
2 µs g
where µs is the coefficient of static friction.
S 10-10
b)
Evaluate this expression when: vo = 67.11 mph and µs = 0.80 .
N

Δr
f = µs N
mg
a)
We treat the static friction like the kinetic and write
=cos180°=−1

W f s = (µ s mg) ( min )( cos∠between ) = −µ s mg min .
(1)
As this is the only force doing work, we have
and, therefore,
=0

1 2
W f s = K − K o = − mv = −µ s mg min ,
2
 min
(2)
v2
=
.
2 µs g
(3)
10-16)

Δr
xo
ksp
m
N
F sp
fk
mg
A block of mass m is pushed against a spring of spring constant ksp compressing it a
distance xo from its natural equilibrium position, as represented in the diagram above. The block
is on a level, rough surface for which the coefficient of kinetic friction is signified by µk . Do the
following:
a)
Use work-energy methods to derive expressions for the following quantities of interest:
i) The speed of the block at the instant the spring is compressed a distance
x = xo / 2 .
ii) The speed of the block at the instant the block loses contact with the spring.
iii) The total distance the block slides before coming to rest.
b)
Calculate values for the quantities of interest given in part a) if:
m = 0.500 kg ; k sp = 80 N / m ; xo = 0.20 m ; µk = 0.400 .
S 10-11
a)
From the free-body diagram, we can write
=0
=0
=0



WN + WG + Wsp + W fk = K L − K o ,
(1)
The work done by the elastic spring is given by
Wsp = U o −U L =
sp
sp
1
2
2
k sp ⎡⎣ xo − x L ⎤⎦ .
2
(2)
The work done by the constant kinetic friction is given by
=cos180°=−1



 
•
W f k = F Δr = ( µ k mg )( )( cos∠bet ) = − µk mg .
(3)
Equations (2) and (3) in equation (1) gives us
1
1 2
2
2
ksp ⎡⎣ xo − xL ⎤⎦ − µk mg = mv ,
2
2
and, in general,
ksp
⎡⎣ xo2 − x 2L ⎤⎦ − 2 µk g .
m
v=
i)
ksp
2
3ksp x o
⎡ x − ( xo / 2 ) ⎤ − 2 µ k g ( x o / 2) =
⎦
m ⎣
For  = x o and x L = 0 , equation (5) becomes
2
2
o
ksp
4m
− µ k gxo .
(6)
2
k sp xo
⎡ x − 0 ⎤⎦ − 2 µ k gxo =
− 2 µ k gxo .
m ⎣
m
We have v = 0 when  =  max , and equation (7) becomes
v=
iii)
(5)
For  = x L = xo / 2 , equation (5) becomes
v=
ii)
(4)
2
o
(7)
2
ksp xo
0=
m
− 2 µ k g max ,
(8)
which implies
2
0=
and, therefore,
k sp x o
m
− 2 µk g max ,
(9)
2
 max =
ksp xo
.
(10)
2 µ k mg
10-17) If the power P supplied to an object of mass m is constant, show that distance traveled in
a straight line is given by
⎡ 8Pt 3 ⎤
Δx = ⎢
⎥
⎣ 9m ⎦
The instantaneous velocity is defined by
S 10-12
1/2
.

 
dv 
P = F• v = m • v ,
dt
(1)
P
 
dt = dv • v ,
m
(2)
which can be rearranged into the differential equation
the solution of which is found by integration
t
v
P
1 2
  P
dt = ∫ dv • v = t = v .
∫
m t=0
m
2
0
(3)
From equation (3) we have
v=
dx
=
dt
2P 1/2
t ,
m
(3)
which leads to the differential equation
dx =
2P 1/2
t dt ,
m
(4)
the solution of which is found by integration. We have
x
∫ dx =
xo
t
2P
1/2
∫ t dt = Δx =
m 0
2P
m
⎡ 2 3 /2 ⎤
⎢ 3t ⎥ =
⎣
⎦
8Pt 3
.
9m
(5)
10-18) The F5 E fighter jet has a power plant that can generate 10,000 lb ( 44.5 kN ) of
thrust and can fly at Mach 1.6 (1.6 times the speed of sound). The newer F5 G generates
16,000 lb ( 71 kN ) of thrust and can fly at Mach 2.1. If the speed of sound is 330 m / s ,
calculate the peak horsepower of each aircraft.
Using the definition of the instantaneous power, we have
PF 5 E = Fv = (44.5 (1,000 ) N )(1.6 (330 m / s )) = 2.35 ×10 7 Watts
≡ 3.15 × 10 4 hp .
(1)
For the newer version, we have
PF 5 G = Fv = ( 71(1,000 ) N )( 2.1( 330 m / s )) = 4.92 × 107 Watts
≡ 6.60 × 104 hp .
(2)
10-19) A 2000 kg elevator is attached to a 1800 kg counter-weight. Calculate the power a
motor must supply to raise the elevator at a constant speed of 0.40 m / s .
The mechanical energy of this system is given by
E=
So,
1
( me + mcw ) v 2 + (m e − mcw ) gh .
2
P = dE / dt = ( me + mcw ) va + ( me − mcw ) gv .
S 10-13
(1)
(2)
As the acceleration is zero, we have
(
)
P = ( 2,000 kg −1,800 kg ) 9.81 m / s 2 (0.40 m / s ) = 785 Watts .
(3)
10-20)
N

T
fk
15°
mg
A winch drags a 200 kg box along a 15° incline at a constant speed of 0.50 m / s . The
coefficient of kinetic friction is µk = 0.20 . Do the following:
a)
Calculate the power required to move the box up the incline.
b)
Calculate the power required to move the box down the incline.
a)
Using the free-body diagram, we can write
T − mg ( sin θ + µ k cos θ ) = 0 ,
(
)
and
T = mg sin θ + µ k cos θ .
So, the power required is given by
P = ⎡⎣ mg ( sinθ + µ k cos θ )⎤⎦ v (cos 0°) = ⎡⎣ mg ( sin θ + µ k cosθ ) ⎤⎦ v
= ⎡⎣( 200) 9.81 m ⋅ s −2 (sin15° + ( 0.20 ) cos15° )⎤⎦ ( 0.5 ) W = 443 W .
(
b)
so
)
(1)
(2)
(3)
mg (sinθ − µ k cos θ ) − T = 0 ,
(4)
T = mg ( sin θ − µ k cos θ ) ,
(5)
and the power is
P = ⎡⎣ mg ( sinθ − µ k cos θ )⎤⎦ v (cos180°) = − ⎡⎣ mg ( sinθ − µk cosθ )⎤⎦ v
(
)
= − ⎡⎣(200 ) 9.81 m ⋅ s −2 ( sin15° − ( 0.20 ) cos15° ) ⎤⎦ ( 0.5 ) W =−64 W .
(4)
10-21) A 60 kg skydiver is falling at the terminal speed of 55 m / s . Calculate the power
dissipated by the air resistance.
War + WG = ΔK = 0 ,
(1)
and
 
Par = F • v = ( mg ) (v )( cos180°)
S 10-14
(
)
= −mgv = − ( 60 kg) 9.81 m ⋅ s −2 (55 m / s ) = −3.24 × 10 4 W = −43.4 hp .
(2)
10-22) A locust can propel its body (≈ 3 grams ) from rest to 3.4 m / s in 4 cm . Estimate
the average power output of the locust’s legs.
The average power is defined by
ΔW
Δr
=F
= mavave .
Δt
Δt
(1)
1
( v + 0) = v / 2 .
2
(2)
a =v/t .
(3)
v = at ,
x = (1 / 2 ) at 2 .
(4)
(5)
v 2
2x
= → t =
.
x t
v
(6)
a = v / (2x / v ) = v 2 / 2x .
(7)
Pave =
The average velocity is given by
vave =
The acceleration is given by
To find t , recall that
while
Dividing equation (4) by equation (5) yields
Substitution of (6) into equation (3) gives
Therefore,
⎡ v 2 ⎤ ⎡ v ⎤ mv 3 ( 0.003)( 3.4 )
Pave = m ⎢ ⎥ ⎢ ⎥ =
=
W = 0.74 W .
4 (0.04 )
⎣ 2x ⎦ ⎣ 2 ⎦ 4 x
3
(8)
10-23) A 2 kg block moves on a circular path of constant radius 1.2 m . In one revolution, the
speed decreases from 8 to 6 m / s . Calculate how many more revolutions the block makes
before coming to rest.

v
N O.O.P.
mg Into Page
Frad
ϕ̂
f
k̂
R
r̂
O.O.P.
As the object is moving on a circular path, there must be a radial force; and, as it is slowing
down, there must be some frictional force opposite the motion. The normal force and the
gravitational force must be perpendicular to the plane of the motion. So, the only force doing work
S 10-15
is the dissipative frictional force. So, we can write
W f = − f ( 2π nR ) =
(
)
1 2 1 2
1
2
2
mv L − mvo = − m vo − v L ,
2
2
2
(1)
where n signifies the number of revolutions; the quantity of interest. Solving equation (1) for n
we find
n=
(
m vo2 − v 2L
2 (2π R ) f
).
(2)
Therefore, assuming a constant dissipative force, the ratio of equation (2) for the second interval to
the first interval gives us
n ⎡ 62 − 02 ⎤
=
= 1.29 .
1 ⎢⎣ 82 − 62 ⎥⎦
(3)
10-24)
ksp
U oG = mgh

m
h =  sin θ
U LG = 0
θ
53°
N

Δr f
Fsp
mg
Represented in the diagram above is a 2 kg block on an incline attached to a massless spring
with spring constant 20 N / m . The coefficient of kinetic friction is µk = 1 / 6 . The block
starts from rest with the spring in equilibrium. Do the following:
a)
After the block slides 40 cm , calculate the following:
i) the work done by the spring;
ii) the work done friction;
iii) the work done by gravity;
iv) the speed of the block.
b)
Calculate the maximum extension of the spring.
a) i)
The work done by the spring, in general, is given by
(
)
2
2
2
Wsp = U osp −U sp
L = (1 / 2 ) ksp x o − x L = − (1 / 2 ) ksp 
= − (1 / 2 ) (20 N )( 0.40 m) = −1.6 J .
2
ii)
(1)
The work done
 by friction is given by

W f = Ff • Δr = ( µk mg cos θ )( ) (cos180° ) = − µ k mg cosθ
(
)
= − (1 / 6 ) (2 ) 9.81 m ⋅ s −2 (0.40 m )( cos53°) = −0.79 J .
S 10-16
(2)
iii) As the gravitational force is conservative, we can use its potential energy to calculate the
work done. In general, then,
(
=0

WG = U − U GL = mg sin θ
= (2 ) 9.81 m ⋅ s
G
o
−2
)( 0.40)( sin 53°) = 6.27 J ,
(3)
where I have set the lower, later gravitational potential energy equal to zero.
iv) In general, the speed is found by calculating the total work done and equating it to the
change in kinetic energy. Noting that the normal force does no work in this process, we have
mg sinθ − µk mg cos θ − (1 / 2 ) ksp  2 = (1 / 2 ) mv 2 ,
(4)
and, therefore,
v = 2g (sin θ − µ k cos θ ) −
ksp

m
2
⎛ 20 ⎞
2
= 2 ( 9.81)( 0.40 ) ⎡⎣ sin 53° − (1 / 6) cos 53°⎤⎦ − ⎜ ⎟ ( 0.40 ) m / s = 1.97 m / s . (5)
⎝ 2⎠
b) To find the maximum distance the spring moves, we note that  =  max when v = 0 . So,
equation (5) becomes
0 = 2g max ( sin θ − µk cosθ ) −
k sp
m
2
 max ,
(6)
which implies
2g max ( sinθ − µk cosθ ) =
and, therefore,
 max =
=
k sp
m
2
 max ,
(7)
2mg
(sin θ − µ k cos θ )
k sp
2 (2 ) (9.81)
(sin 53° − (1 / 6 ) cos 53°) m = 1.37 m .
( 20 )
(8)
10-25)
Fsupport
U LG = 0
m1
U oG = m1g

m2
m2
m1
m2 g
U oG = −m2 g
U LG = 0
m1 g
Two blocks of masses m1 = 5 kg and m2 = 2 kg hang on opposite sides of a frictionless
S 10-17
cylinder, as represented in the diagram above. If the system is released from rest, calculate the
speed of each block at the instant each block has moved a distance 40 cm .
The choice of a system can sometimes simplify things. In this problem, I am going to let the
system be comprised of the two blocks, the cylinder and the string. For this system, the only
external forces acting on the system are the support force--which does no work as it does not
displace any physical thing--and the conservative gravitational force. Therefore, we can use the
conservation of mechanical energy. To that end, we write
=0
=0


K o + UoG = K L +U LG ,
(1)
and
m1 g − m2 g =
Therefore,
1
( m1 + m2 ) v 2 .
2
⎡ m − m2 ⎤
⎡5 − 2⎤
v = ⎢ 1
⎥ 2g = ⎢
⎥ 2 ( 9.81)( 0.40 ) m / s = 1.83 m / s .
m
+
m
5
+
2
⎣
⎦
⎣ 1
2 ⎦
(2)
(3)
(Had there been friction between the string and the cylinder, we would have had to include the
rotational kinetic energy of the cylinder.)
10-26)
m2
m1
Two blocks of masses m1 = 0.50 kg and m2 = 1.50 kg are connected by a light string,
as represented in the diagram above. The pulley and horizontal surface are frictionless. If the
blocks are released from rest, calculate the speed of each block at the instant each has moved
60 cm .
With a similar choice of system as used in the preceding problem, we can use the
conservation of mechanical energy and write
m1 g =
and, therefore,
1
( m1 + m2 ) v2 ,
2
(1)
⎡ m1 ⎤
⎡ 0.5 ⎤
v = ⎢
⎥ 2g = ⎢
⎥ 2 ( 9.81)( 0.60 ) m / s = 1.72 m / s . (2)
⎣ 0.5 + 1.5 ⎦
⎣ m1 + m2 ⎦
10-27)
Two blocks of masses m1 = 4.0 kg and m2 = 5.0 kg are connected by a light
string and slide on a frictionless wedge, as represented in the diagram below. The system starts
S 10-18
from rest. Calculate the speed of each block at the instant each has moved 40 cm along the
wedge.
m1
m2
53°
37°
We again use the conservation of mechanical energy noting that block two will have a
component of motion vertically downward and block one a component vertically upward.
U o = m1g sin 53° − m2 g sin 37° = K L =
G
Therefore,
1
( m1 + m2 ) v 2 .
2
(1)
⎛ m sin 53° − m2 sin 37° ⎞
v = ⎜ 1
⎟⎠ 2g m1 + m2
⎝
⎛ 5 ( sin 53°) − 4 (sin 37°)⎞
m
m
(
)
(
)
= ⎜
2
9.81
0.40
=
1.18 .
⎟⎠
⎝
5+4
s
s
(2)
10-28)
ϕo
30°
 cos ϕ o
 cos ϕ


v
m
U LG = 0
ho
ϕo
ϕ
T
ϕ̂
mg
r̂
A simple pendulum has a light string of length  = 0.75 cm and a “bob” of mass 0.6 kg
attached to one end of the string. The other end of the string is attached to a frictionless pivot. If
released from rest, the bob has a speed 2 m / s when the string makes an angle of 30° to the
vertical. Do the following:
a)
Calculate the maximum speed of the bob.
b)
Calculate the maximum angle the string makes to the vertical.
a)&b) The free-body diagram indicates that two forces are acting on the bob. The tension, however,
S 10-19
does no work as it is always perpendicular to the displacement. So, we can use the conservation of
mechanical energy and write
=0 
=0



2
2
(1 / 2 ) mvo + mgho = (1 / 2 ) mv + mghL ,
and
v = 2gho .
Careful inspection of the free-body diagram should convince one that
ho =  cosϕ − cos ϕ o =  (cos ϕ − cos ϕ o ) .
(1)
(2)
(3)
So, equation (2) becomes
v = 2g (cos ϕ − cos ϕ o ) .
(4)
The maximum speed is attained when ϕ = 0 . However, to use equation (4), we need to know
ϕ o . To that end, we use equation four and the fact that we know the speed when the angle is thirty
degrees.
v2
v = 2g ( cos ϕ − cosϕ o ) → cos ϕ − cos ϕ o =
,
2g
(5)
⎡
⎤
( 2 )2
⎡
v2 ⎤
−1
ϕ o = cos ⎢ cosϕ −
=
cos
cos
30°
−
⎢
⎥ = 53.5° .
2g ⎥⎦
2 (9.81) (0.75 ) ⎥⎦
⎣
⎢⎣
(6)
vmax = 2 (9.81 )(0.75 )( cos0° − cos 53.5°) = 2.44 m / s .
(7)
2
Therefore,
−1
Now, we can find the maximum speed. We have
10-29) A block of mass m = 0.25 kg can slide on a frictionless, horizontal surface. It is attached
to a massless spring with spring constant ksp = 10 N / m . The block is pulled 40 cm from the
spring’s equilibrium position and released. Do the following:
a)
Calculate the maximum speed of the block.
b)
Calculate the speed of the block when the spring is extended 20 cm .
c)
Calculate the position of the block, relative to equilibrium, when the kinetic energy
of the block is equal to elastic potential energy of the spring.

Δr
N
Fsp
mg
a) The only force that does work on the block is the conservative elastic potential energy. So, we
can write
=0

K o + (1 / 2 ) ksp xo2 = (1 / 2) mv2 + (1 / 2) ksp x 2L ,
S 10-20
(1)
and the speed is given by
(x
m
ksp
v=
2
o
)
− xL .
2
(2)
The maximum speed is obtained at the instant xL = 0 . Therefore,
vmax =
b)
(x
m
k sp
2
o
(10 )(0.40 )2
)
− 0 =
v=
m
(x
2
o
− ( xo / 2)
2
) = (3)
3 (10 )( 0.40 ) m
m
= 2.19 .
4 (0.25 )
s
s
(4)
0.25
The speed when xL = xo / 2 , gives us
ksp
m
m
= 2.53 .
s
s
2
3ksp x o
4m
2
=
10-30)
m
m
60 cm
ho
xm
ksp
U LG = 0
ksp
A 500 gram block is dropped from a height of 60 cm above the top of a massless,
vertical spring in equilibrium, as represented in the diagram above. The spring constant is given by
ksp = 120 N / m . Calculate the maximum compression of the spring.
We use the conservation of mechanical energy since the only forces acting on the block are
the conservative gravitational and elastic spring forces. There is no change in kinetic energy over
this interval as both the initial and final speed is zero. We also set the later gravitational potential
energy to zero. So, we have
=0
=0
=0
=0




G
sp
K o + Uo +U o = K L +U LG + U Lsp ,
(1)
and
mg (ho + xm ) =
1
2
ksp xm .
2
(2)
Equation (2) yields a quadratic equation in xm .
(1 / 2 ) k sp x m2 − mgx m − mgho = 0 ,
S 10-21
(3)
which, after some algebra to get the coefficient of the quadratic term to be one, becomes
⎡ mg ⎤
⎡ mg ⎤
xm2 − 2 ⎢ ⎥ xm − 2ho ⎢
⎥=0.
k
k
⎢⎣ sp ⎥⎦
⎢⎣ sp ⎥⎦
(4)
The only physically meaningful root of this equation is given by
2
⎡ mg ⎤
⎡ mg ⎤
⎡ mg ⎤
xm = ⎢ ⎥ + ⎢ ⎥ + 2ho ⎢
⎥ k
k
k
⎢⎣ sp ⎥⎦
⎢⎣ sp ⎦⎥
⎢⎣ sp ⎥⎦
⎡ ( 0.5 )( 9.81) ⎤
⎡ ( 0.5 )( 9.81) ⎤
⎡ ( 0.5 )( 9.81) ⎤
=⎢
m + ⎢
+ 2 (0.60 ) ⎢
⎥
⎥
⎥ m
120
120
120
(
)
(
)
(
)
⎣
⎦
⎣
⎦
⎣
⎦
= 0.266 m .
2
(5)
10-31) A simple pendulum of length  with a “bob” of mass m is released from rest when the
string is horizontal. The string has a breaking tension Tb . Do the following:
Derive an expression for the angle ϕ b at which the string will break.
Calculate the value of this angle if:
 = 1.25 m ; m = 0.50 kg ; Tb = 6 N
(A free-body diagram is always helpful.)
a)
b)

m
ϕ
T
ϕ̂
mg cos ϕ
ϕ
mg
r̂
by
From earlier work, we know that if the initial speed is zero, then the speed of the bob is given
v = 2g (cos ϕ − cos ϕ o ) = 2g cos ϕ ,
(1)
as ϕ o = 90° , while the angle is related to the speed by
cos ϕ = v 2 / 2g .
(2)
Using Newton’s second law for circular motion, we have
Equation (2) implies
mv 2
mv2
mg cos ϕ − T = −
→ T = mg cosϕ +
.


S 10-22
(3)
Equation (4) in equation (3) yields
mv2
= 2mg cos ϕ .

(4)
T = mg cos ϕ + 2mg cos ϕ = 3mg cos ϕ .
So, when T = Tb , then ϕ = ϕ b , and equation (5) gives us
Tb = 3mg cos ϕ b ,
(5)
(6)
and
b)
⎡ T ⎤
ϕ b = cos−1 ⎢ b ⎥ .
⎣ 3mg ⎦
(7)
⎡
⎤
6
ϕ b = cos−1 ⎢
⎥ = 66° .
⎣ 3 (0.5 ) 9.81 ⎦
(8)
For the values given we have
10-32)
ksp
m
Fsp
M
N
mg Fsupport
Mg
A block of mass m slides on a frictionless, horizontal surface and is connected to a massless
spring with spring constant ksp . A second block of mass M is attached to the first block by a
light string that passes over a frictionless pulley, as represented in the diagram above. The system
is released from rest. Do the following:
a)
Derive an expression for xmax , the maximum extension of the spring.
b)
Derive an expression for the speed of each block at the instant the spring has been
extended a distance x , where x < x max .
c)
Calculate the values of interest in parts a) and b) if:
M = 2m = 4 kg ; k sp = 40 N / m ; x = 50 cm .
Again, we choose both masses, the pulley and the light string as the system. The support
force on the pulley does no work as it does not displace any physical thing. The normal force on
the sliding block does no work as it is everywhere perpendicular to the displacement. So, only the
conservative gravitational and elastic spring forces do work. We use the conservation of mechanical
energy and write
b)
and
=0
=0
=0



1
1
sp
2
G
2
K o + Mgx + Uo = ( M + m ) v + U L + k sp x ,
2
2
S 10-23
(1)
v=
2Mgx − k sp x
2
.
M +m
(2)
a) The maximum extension of the spring, xm , occurs at the instant v = 0 . Subject to these
conditions, equation (2) requires
2Mgxm − ksp xm2 = 0 ,
(3)
and, therefore,
2Mg
.
k sp
(4)
2Mg 2 ( 4 ) (9.81)
=
m = 1.96 m ,
k sp
40
(5)
xm =
c)
For the values given,
xm =
v=
while
2Mgx − k sp x
2
M +m
2 ( 4 ) (9.81) (0.50 ) − (40 ) (0.50 ) m
m
= 2.21 .
4+2
s
s
2
=
10-33)
Fsup1
m
(6)
Fsup2
M
ksp
Fsp
mg
Mg
Two blocks of masses m and M are connected by a light string which passes over two
frictionless pulleys. Mass m is also attached to a massless, vertical spring of spring constant ksp ,
as represented in the diagram above. Assume the system is released from rest with the spring in its
equilibrium position. Do the following:
a)
Derive an expression for xmax , the maximum extension of the spring.
b)
Derive an expression for the speed of each block at the instant the spring has been
extended a distance x , where x < x max .
c)
Calculate the values of interest in parts a) and b) if:
M = 5 kg ; m = 3 kg ; ksp = 32 N / m ; x = 1 m .
S 10-24
Again, we choose both masses, the pulleys and the light string as the system. The support
forces on the pulleys do no work as no physical thing is displaced. So, only the conservative
gravitational and elastic spring forces do work. We use the conservation of mechanical energy and
write
=0
=0
=0



1
1
sp
2
G
2
K o + M − mgx + Uo = ( M + m ) v + U L + k sp x ,
2
2
b)
and
v=
2 ( M − m ) gx − k sp x
(1)
2
.
M +m
(2)
a) The maximum extension of the spring, xm , occurs at the instant v = 0 . Subject to these
conditions, equation (2) requires
2 ( M − m ) gx m − k sp x m2 = 0 ,
(3)
and, therefore,
2( M − m) g
.
k sp
(4)
2 ( M − m ) g 2 (5 − 3) (9.81)
=
m = 1.23 m ,
k sp
32
(5)
xm =
c)
For the values given,
xm =
v=
while
2 ( M − m ) gx − k sp x
2
M +m
2 ( 5 − 3)( 9.81)(1.0 ) − ( 32) (1.0 ) m
m
= 0.95 .
5+3
s
s
2
=
(6)
10-34)
Before Hitting The Spring
m

N
fk
ksp
After Hitting The Spring
N
mg
F sp
fk
mg
θ
A block of mass m is released from rest and slides a distance  before striking a massless,
elastic spring in equilibrium. The spring constant is ksp . The surface on which the block slides is
S 10-25
inclined, with respect to the horizontal, an angle θ and the coefficient of kinetic friction is µk . Do
the following:
a)
Derive an expression for vmax , the speed of the block when it strikes the spring.
b)
c)
a)
Derive an expression for xmax , the maximum compression of the spring.
Calculate the values of interest in parts a) and b) if:
m = 1 kg ; ksp = 100 N / m ;  = 4 m ; θ = 30° ; µ k = 0.30 .
Before striking the spring, the forces involved lead to a general work equation given by
and
=0
=0
=0



WN + WG + Wsp + W fk = K L − K o ,
(1)
mg sinθ − µk mg cos θ = (1 / 2 ) mv 2max ,
(2)
and
v = 2g (sin θ − µ k cos θ ) .
(3)
b) After the collision, maximum compression, occurs at the instant the block stops. So, if one
uses the entire interval from start to end, we can rewrite equation (1) as
=0
=0
=0



WN + WG + Wsp + W fk = K L − K o .
(4)
The work done by gravity is given by
=0

G
WG = U − U L = mg ( x max + ) sinθ = mg (sin θ ) xmax + mg sin θ .
G
o
(5)
The work done by the spring is given by
=0

2
Wsp = U osp −U GL = − (1 / 2 ) k sp x max
.
(6)
The work done by the kinetic friction is given by
W f k = −µ k mg cos θ ( x max +  ) = −µ k mg ( cosθ ) xmax − µ k mg cosθ .
Adding up all of the work and collecting terms in descending orders of xmax , we have
− (1 / 2 ) k sp x 2max + mg ( sin θ − µk cosθ ) xmax + mg (sin θ − µ k cos θ ) = 0 .
(7)
(8)
In order to get the coefficient of the quadratic term to be a positive one, we multiply all terms
by −2 / k sp and getting
⎡ mg
⎤
⎡ mg
⎤
2
( sin θ − µk cosθ )⎥ x max − 2 ⎢ (sin θ − µ k cos θ )⎥ = 0 .
xmax
− 2⎢
⎢⎣ ksp
⎥⎦
⎢⎣ k sp
⎥⎦
mg
( sin θ − µ k cosθ ) .
If we let
C=
ksp
we can rewrite equation (9) as
2
xmax
− (2C ) x max − 2 ( C ) = 0 .
The only physically meaningful root to this quadratic equation is given by
S 10-26
(9)
(10)
(11)
xmax = C + C 2 + 2C .
c)
(11)
For the values given,
vmax = 2g ( sinθ − µ k cos θ )
m
m
= 2 ( 9.81)( 4 ) (sin 30° − (0.30 ) cos30° ) = 4.34 .
s
s
First, we calculate the value of C . We find
mg
( sin θ − µ k cosθ )
C=
ksp
=
Finally, then,
(1)( 9.81)
100
(12)
( sin 30° − (0.30 ) cos30°) m = 0.023563 m .
(13)
xmax = C + C 2 + 2C
= 0.023563 m +
(0.023563)2 + 2 ( 4 )( 0.023563) m = 0.46 m
.
(14)
10-35) A point mass m is launched vertically upward with an initial speed vo from the surface of
the Earth. Ignore the air resistance and the Earth’s rotation in doing the following:
a)
Derive an expression for vesc , the minimum speed required of an object to escape being
bound to the Earth’s gravitational force. Hint: assume the speed of the rocket vanishes
at infinity.
b)
Calculate the value of vesc if:
M ⊕ = 5.97 × 10 24 kg ; R⊕ = 6.371 × 106 m ; G = 6.67 ×10 −11 N ⋅ m 2 ⋅ kg −2 .
a) & b) Using the conservation of mechanical energy an assuming that both the kinetic and
gravitational potential energies are zero later, at infinity, then we can write
1 2
GmM ⊕
mvesc −
=0,
2
R⊕
and, therefore,
vesc =
(
(1)
)(
)
2 6.67 × 10−11 N ⋅ m 2 ⋅ kg −2 5.97 × 1024 kg
2GM ⊕
= R⊕
6.371 × 10 6 m
(
= 1.12 ×10 4 m / s ≡ 25,000 mph .
)
(2)
10-36) A point mass m is launched vertically upward and reaches a maximum height hmax .
Ignore air resistance and the Earth’s rotation when calculating the height h at which the kinetic
G
energy is seventy-five percent of the gravitational potential energy. (Use U = mgh .)
Using the conservation of mechanical energy, we can write, for the interval from launch to
S 10-27
maximum height,
K o + UoG = K L +U LG ,
and
(1 / 2 ) mvo2 + 0 = 0 + mghmax
(1)
.
(2)
Now, if we look at a second interval from launch to a point at a height h where K = ( 3 / 4 )U ,
then we can write
(1 / 2 ) mvo2 = mghmax = ( 3 / 4 ) mgh + mgh = ( 7 / 4 ) mgh .
(3)
Therefore,
h = ( 4 / 7 ) hmax .
(4)
G
10-37)

vo
60°
40 m
A small mass m is launched at 25 m / s in a direction 60° above the horizontal from a
rooftop 40 m above level ground, as represented in the diagram above. Ignoring air resistance, do
the following:
a)
Calculate the speed of the projectile at the instant it strikes the ground.
b)
Calculate the height of the projectile when its speed is 15 m / s .
(Remember, we are using work-energy methods in this chapter!)
U
G
As we are ignoring air resistance, we can use the conservation of mechanical energy. Setting
= 0 at ground level, we can write
(1 / 2 ) mvo2 + mgho = (1 / 2 ) mv 2 + mgh ,
(1)
and
v = v2o + 2g (ho − h ) .
(2)
For the values given, we have
v=
(25 )2 + 2 (9.81) (40 − 0 ) m / s = 37.5 m / s .
(3)
b) We can rearrange a squared version of equation (2) to derive an equation for the height at
which the speed is 15 m / s . We find
2g ho − h = v 2 − vo2 ,
(4)
and
(
)
(
)
h = ho + ⎡⎣ vo2 − v 2 / 2g ⎤⎦ ,
S 10-28
(5)
and
{
(
}
)
h = 40 + ⎡⎣ 25 2 −15 2 / 2 ( 9.81)⎤⎦ m = 60.4 m .
(6)
10-38) An object of mass m is launched vertically upward with a speed of vo from the surface of
the Moon. Calculate the minimum value for vo such that the object never returns to the Moon due
to the Moon’s gravitational force. Such a speed is called the escape speed, vesc . Assume air
resistance is negligible, easy as the Moon has virtually no atmosphere, and ignore any lunar
rotation. (Hint: it is as if the object does not stop until it is infinitely far from the Moon.)
Using the conservation of mechanical energy an assuming that both the kinetic and
gravitational potential energies are zero later, at infinity, then we can write
1 2
GmM M
mvesc −
=0,
2
RM
and, therefore,
vesc =
(
(1)
)(
)
2 6.67 × 10−11 N ⋅ m 2 ⋅ kg −2 7.36 × 10 22 kg
2GM M
= RM
1.74 × 10 6 m
(
= 2.375 × 103 m / s ≡ 5,300 mph .
)
(2)
10-39) A rocket is fired vertically upward from the Earth’s surface with an initial speed vesc / N
where N > 1 . Show that hmax , the maximum height reached by the rocket is given by
R⊕
,
N2 −1
6
where R⊕ is the average radius of the Earth, given by R⊕ = 6.371 × 10 m . Ignore air resistance
hmax =
and the Earth’s rotation.
Using the conservation of mechanical energy, and what we have learned about the Earth’s
escape speed, we can write
and, simplifying,
Further,
1 ⎡ 2GmM ⊕ ⎤ GmM ⊕
GmM ⊕
m⎢ 2
=−
,
⎥−
2 ⎣ N R⊕ ⎦
R⊕
R⊕ + hmax
(1)
1
1
R⊕
=−
.
2 −1 = −
N
1+ hmax / R⊕
R⊕ + hmax
(2)
1
R⊕
R⊕ + hmax − R⊕
hmax
=
1
−
=
=
.
N2
R⊕ + hmax
R⊕ + hmax
R⊕ + hmax
(3)
So,
(
)
R⊕ + hmax = N 2 hmax → N 2 hmax − hmax = hmax N 2 −1 = R⊕ .
Therefore,
S 10-29
(4)
(
)
hmax = R⊕ / N 2 −1 .
(5)
10-40) T o what radius would the Earth have to collapse for the escape speed to equal the speed of
8
light? Use c = 2.998 × 10 m / s for the speed of light. What would be the average mass
density of such an “Earth”? How does this value compare to the mass density of a proton? (Use
10 −15 m for the radius of the proton.)
We know for the Earth, the escape speed is given by
vesc =
So,
R⊕ =
2GM ⊕
2GM ⊕
2GM ⊕
2
→ c =
→ R⊕ =
.
R⊕
R⊕
c2
(
)(
2 6.67 × 10 −11 5.97 × 1024
( 2.998 × 10
8
m / s
)
2
) m = 8.86 × 10
−3
m .
(1)
(2)
The average mass density of such an object would be
ρave
M⊕
5.97 ×10 24 kg
=
=
( 4 / 3)π R⊕3 ( 4/3) π 8.86 × 10−3 m
(
)
3
= 2.05 × 10 30 kg
.
m3
(3)
The average mass density of the proton is approximately
ρave
mp
1.673 × 10 −27 kg
17 kg
=
=
4
×10
3 .
3 =
3
m
( 4 / 3)π Rp ( 4/3) π 10 −15 m
(
)
(4)
10-41) A projectile is fired vertically upward from the surface of the Earth with an initial speed vo .
Show that hmax the maximum height above the surface reached by the projectile is given by
hmax
vo2
=
,
2g − vo2 / R⊕
(
)
where g is the acceleration due to the Earth’s gravity and R⊕ is the average radius of the Earth.
Again, we exploit the conservation of mechanical energy and find
1 2 GmM ⊕
GmM ⊕
GmM ⊕ ⎡
1
⎤
mvo −
=−
=−
⎢
⎥ .
2
R⊕
R⊕ + hmax
R⊕ ⎣ 1 + hmax / R⊕ ⎦
Multiplying equation (1) by 2 / m and rearranging terms, we get
2GM⊕ 2GM ⊕ ⎡
1
⎤
⎡
1
⎤
2
vo =
−
⎢
⎥ = 2gR⊕ ⎢1−
⎥,
R⊕
R⊕ ⎣ 1 + hmax / R⊕ ⎦
⎣ 1 + hmax / R⊕ ⎦
(1)
(2)
where we have used the fact that
g = GM ⊕ / R⊕2 .
Working on the bracketed terms, we can write
S 10-30
(3)
⎡
1
⎤ ⎡
R⊕
⎤ ⎡ R⊕ + hmax − R⊕ ⎤
hmax
.
⎢1 −
⎥ = ⎢1 −
⎥= ⎢
⎥=
⎣ 1 + hmax / R⊕ ⎦ ⎣ R⊕ + hmax ⎦ ⎣ R⊕ + hmax ⎦ R⊕ + hmax
(4)
⎡ hmax
2
vo = 2gR⊕ ⎢
⎣ R⊕ + hmax
(5)
So, equation (2) becomes
and
hmax
⎤
R⊕ + hmax 2gR⊕
R
2gR⊕
= 2 → ⊕ =
−1 ,
⎥ → 2
h
v
h
v
⎦
max
o
max
o
R⊕
R⊕ v2o
=
=
2gR⊕
2gR⊕ − vo2
−
1
2
vo
⎡1 / R⊕ ⎤
v2o
.
⎢
⎥=
2
1
/
R
2g
−
v
/
R
⎣
⊕ ⎦
o
⊕
(
)
(6)
10-42) Newton’s second law and his law of universal gravitation when applied to circular orbits
yields
Gm1 m2 m1v12
=
,
r122
r12
use this to do the following:
a)
Derive an expression for the kinetic energy of mass m1 .
b)
Write the appropriate expression for the gravitational potential energy of the two mass
system.
c)
Calculate the change in the kinetic energy of a satellite of mass m initially orbiting the
Earth on a circular orbit of radius 3R⊕ if it is moved to another circular orbit of radius
6R⊕ .
d)
a)
Is the mechanical energy conserved in the re-tasking of the satellite?
The given equation implies
Gm1 m2 m1v12
1
Gm1m2
2
=
→ m1v1 =
.
2
r12
r12
2
2r12
b)
The gravitational potential energy is given by
U =−
G
c)
Gm1 m2
.
r12
(2)
The change in kinetic energy is given by
ΔK = K L − K o =
d)
(1)
GmM ⊕ GmM ⊕
GmM ⊕
−
=−
.
2 (6R⊕ ) 2 ( 3R⊕ )
12R⊕
(3)
If the mechanical energy were conserved, then the work done would by given by
⎡ GmM ⊕ ⎤ ⎡ GmM ⊕ ⎤
GmM ⊕
G
G
G
W = ΔK = −ΔU = Uo −U L = ⎢ −
.
⎥ − ⎢−
⎥=−
6R⊕
⎣ 3R⊕ ⎦ ⎣ 6R⊕ ⎦
For circular orbits, the mechanical energy is not conserved.
S 10-31
(4)
10-43) A ball of mass m moves in a vertical circle at the end of a string of length  , as
represented in the diagram below. Show that the tension in the bottom is greater than the tension at
the top by
6mg .

vT
mg


v
m
TT

TB
mg

vB
Using Newton’s second law, we can write, for the bottom,
v 2B
⎡
vB2 ⎤
mg − TB = −m → T B = m ⎢ g + ⎥ .

 ⎦
⎣
(1)
vT2
⎡
vT2 ⎤
−mg − TT = −m → TT = −m ⎢ g − ⎥ .

 ⎦
⎣
(2)
⎡ ⎛
vB2 ⎞ ⎤ ⎡ ⎛
vT2 ⎞ ⎤
⎡ vB2 vT2 ⎤
TB − TT = ⎢ m ⎜ g + ⎟ ⎥ − ⎢ −m ⎜ g − ⎟ ⎥ = 2mg + m ⎢ − ⎥ .
 ⎠⎦ ⎣ ⎝
 ⎠⎦
 ⎦
⎣ 
⎣ ⎝
(3)
v2B vT2
(1 / 2 ) mv = (1 / 2 ) mv + 2mg → − = 4g .


(4)
TB − TT = 2mg + m [ 4g ] = 6mg .
(5)
for the top, we write
The difference, then, is
Using the conservation of mechanical energy, we can write, assuming the gravitational
potential energy at the bottom is zero,
2
B
2
T
Equation (4) in equation (3) gives us
10-44) A simple pendulum with a light string of length  and “bob” of mass m has its motion
interrupted by a horizontal peg a distance y directly below the pivot, as represented in the diagram
below. The bob is released when the string is horizontal. Show that for the bob to swing in a
complete circle, the minimum value of y is (3 / 5 )  .
The motion of the mass, once the string makes contact with the peg, is circular with a radius
R =  − y . The minimum value of y for a complete circle occurs when the tension at the top of
S 10-32
is zero. The tension is given by
mg cos ϕ − T = −mv 2 / R → v2 = RT − Rg cos ϕ .
m

(1)

m
y
y
R
T
ϕ

v
mg
r̂
The tension is zero at the instant the bob is at the top of the “completed” circular path. At
that instant, ϕ = 180° and v = vtop and the speed at the top is given by
2
vtop
= RT − Rg cos ϕ = R ( 0) − Rg cos180° = Rg .
(2)
Next, we use the conservation of mechanical energy over the interval of release to the instant the bob
is at the top of the completed circular path and arbitrarily set the gravitational potential energy equal
to zero at the bottom of the bob’s path of motion. We have
K o + UoG = K L +U LG ,
(3)
and
0 + mg =
Therefore,
1
5
2
2
m ( Rg ) + mg ( 2R ) = mRg → R =  →  − y =  .
2
2
5
5
(4)
2
3
 = .
5
5
(5)
y = −
10-45) A small mass m is at rest in unstable equilibrium at the top of a smooth hemisphere of
radius R , as represented in the diagram below. A very small perturbation initiates motion of the
point mass at negligible speed. Do the following:
a)
Calculate θ m , the angle, measured to the vertical at which the small mass would lose
contact with the hemisphere.
b)
Calculate d , the horizontal distance from the center of the hemisphere at which the
point mass strikes the ground.
The small mass moves on a circular path of radius R and Newton’s second law implies
N − mg cosθ = −mv 2 / R .
(1)
At some point P the point mass losses contact with the sphere and the normal N vanishes. The
speed squared at this point is given by
vm2 = Rg cosθ m .
(2)
Next, as the normal force does no work, we can use the conservation of mechanical energy
S 10-33
a)
over the interval from the start to the point at which contact is lost; the point at which the mass
becomes a projectile.
r̂
()
y ĵ
U = mgho
θ̂
N
m
G
o
ho

v
mg
R
θ
θm
U LG = 0
θm
R
R sin θ m
()
x î
d
K o + UoG = K L +U LG ,
1
m ( Rg cos θ m ) + 0 = mgR(1 − cos θ m ) ,
2
cos θ m = 2 (1− cos θ m ) → 3cos θ m = 2 .
0 + mgho =
and
while
Therefore,
b)
(3)
(4)
(5)
θ m = cos −1 [ 2 / 3] = 48.2° .
The distance d we will find in terms of R . Also, as cos θ m = 2 / 3 , this implies
(6)
sinθm = 1 − cos 2 θ m = 1 − (2 / 3) = 5 / 9 = 5 / 3 .
2
(7)
At the beginning of the projectile phase, the projectile has a speed given by
vm =
Rg cosθ m =
( 2 / 3) g R = 2.557 R ,
(8)
(I am not going to show the units, but remember this coefficients do have units.)Setting up our
table, we have

ro

vo

a
x
y
R sin θ m
R cosθ m
vm cosθ m
− vm sinθ m
0
−g
(9)
The coordinate equations of motion are given by
x = R sin θ m + vm ( cosθ m )t ,
and
y = R cosθ m − v m ( sin θ m ) t − (1 / 2 ) gt 2 .
S 10-34
(10)
(11)
We note that the value of interest, d , can be found using equation (10) when t = t f , the so-called
time of flight. We also know that y = 0 when t = t f . Equation (11) becomes
0 = R cosθ m − vm (sin θ m )t f − (1 / 2 ) gt 2f .
(12)
We multiply equation (12) by −2 / g to get the coefficient on the quadratic term to be one. We
find
t 2f + 2 ⎡⎣ vm ( sinθ m ) / g ⎤⎦ t f − 2R cosθ m / g = 0 .
(13)
The only physically meaningful root is
v ( sin θ m )
⎡ v ( sinθm ) ⎤ 2R cosθ m
tf = − m
+ ⎢ m
⎥ +
g
g
g
⎣
⎦
2
(2.557 R )(
=−
5/3
) + ⎡⎢( 2.557 R ) (
⎢
⎣
9.81
)
2
5/3 ⎤
4
⎥ +
R 9.81
⎥ 3 (9.81)
⎦
2
= −0.19428 R + ⎡⎣−0.19428 R ⎤⎦ + 0.13592 R = 0.22245 R . (14)
Back to d .
=R
(
d = R sin θ m + vm (cos θ m ) t f
) (
)
(
)
5 / 3 + 2.557 R (2 / 3) 0.22245 R = 1.125 R .
10-46)
()
y ĵ

C
B

O

A
()
x î
A force varies as F ( x , y) = xy î . Perform the integration of
2
 
W = ∫ F • dr
from O to B along the following paths:
a)
From O to A then A to B .
S 10-35
(15)
b)
c)
a)
From O to C then C to B .
Is the force conservative?
In going from O to A ,

dr = dx î ,
and
WO→ A = ∫ xy î dx î = (0 )
2
•
In going from A to B ,
and
Therefore,
b)

2
∫ x dx = (0 ) (
2
)
/ 2 =0.
(2)
0

dr = dy ˆj ,
(3)
WA→ B = ∫ xy 2 î • dy ĵ = 0 .
(4)
WO→ A + WA +B = 0 + 0 = 0 .
(5)

dr = dy ˆj ,
(6)
WO→C = ∫ xy 2 î • dy ĵ = 0 .
(7)

dr = dx î ,
(8)
In going from O to C ,
and
(1)
In going from C to B ,
and
WA→ B = ∫ xy î
2
• dx î
= ( )

2
∫ x dx = 
4
/2.
(9)
0
Therefore,
WO→C +WC+ B = 0 + 4 / 2 =  4 / 2 .
c)
(10)
As the work done is path dependent, the force is not conservative.
10-47) Repeat the preceding problem for the force

F ( x , y) = 2y 2 î + 3x ĵ .
a)
In going from O to A ,

dr = dx î ,
and
WO→ A =
∫ ( 2y
In going from A to B ,
and
2
î + 3x ĵ
)
•
dx î = 2 (0 )
(1)

2
∫ x dx = (0 ) (
2
)
/ 2 =0.
(2)
0

dr = dy ˆj ,
S 10-36
(3)
WA→ B =
∫ ( 2y
2
î + 3x ĵ
)

• dy ĵ = 3( ) ∫ dy = 3
2
(4)
0
Therefore,
b)
WO→ A + WA +B = 0 + 32 = 32 .
(5)

dr = dy ˆj ,
(6)
In going from O to C ,
and
WO→ A =
∫ ( 2y
2
î + 3x ĵ
In going from C to B ,
•
dy ĵ = 3 (0 ) ∫ dy = 3( 0 )( ) = 0 .
(7)
0

dr = dx î ,
and
WO→ A =
)

∫ ( 2y
2
î + 3x ĵ
)
•
(8)
dx î = 2 ( )
2

∫ dx = 2 ( )( ) = 2
2
3
.
(9)
0
Therefore,
WO→C +WC+ B = 0 + 2 3 = 2 3 .
c)
(10)
As the work done is path dependent, the force is not conservative.
10-48) The potential energy associated with two particles is given by
(
U ( x) = C a2 + x2
)
−1/ 2
,
where C and a are constants. Do the following:

a)
Find the conservative force F .
b)
Calculate the value of x at which the force is a maximum.
a)
As this force is one-dimensional, we can write

d ⎡
2
2
F = −∇U = − î
C a +x
dx ⎣
(
⎤ = − ⎧⎨− 1 C a 2 + x 2
⎦
⎩ 2
Cx
= 2
3/ 2 î .
a + x2
)
(
b)
(
−1/ 2
) ( 2x )⎫⎬⎭ î
−3/ 2
If we take the derivative of equation (1), we find
(
dF
2
2
= C ⎡x a + x
⎣
dx
⎧
1
⎪
=C⎨
2
2
⎪⎩ a + x
(
)
)
3/2
−3/ 2
⎤ = C ⎧⎨ a 2 + x 2
⎦
⎩
(
(1)
)
)
−3/2
⎡ 3 2
2
+ x ⎢− a + x
⎣ 2
(
) ( 2x )⎤⎥⎦ ⎫⎬
−5/2
⎫
⎧ a2 + x 2
3x 2
⎪
⎪
−
−
⎬=C⎨ 2
2
2 5 /2
2 5 /2
2
2
a +x
a +x
⎪⎭
⎪⎩ a + x
(
3x 2
)
(
)
(
⎭
⎫
⎪
5/ 2 ⎬ .
⎪⎭
)
(2)
Equation (2) represents a maximum value, if it has a maximum value, when it is zero. That
would require
S 10-37
Therefore,
a 2 + x 2 = 3x 2 → 2x 2 = a 2 .
(3)
x = ±a / 2 .
(4)
10-49) The electric potential energy shared between an infinite line charge and a charged particle is
given by
U ( r ) = C ln r / a ,
[
]
where r is the perpendicular distance from
 the line charge to the point charge and C and a are
constants. Find the conservative force F .
The force is given by

d ⎡
C
⎛ r⎞⎤
⎡a⎤ d
⎡a⎤⎛ 1⎞
−1
F = −r̂ ⎢ C ln ⎜ ⎟ ⎥ = −C ⎢ ⎥
ra r̂ = −C ⎢ ⎥ ⎜ ⎟ r̂ = − r̂ . (1)
⎝ a⎠ ⎦
dr ⎣
r
⎣ r ⎦ dr
⎣r ⎦⎝ a⎠
(
)
10-50) The potential energy shared between two atoms separated by a distance r in a diatomic
molecule is given by the Lennard-Jones function, where U o and ro are constants:
6
⎡⎛ ro ⎞ 12
⎛ ro ⎞ ⎤
U ( r ) = U o ⎢⎜ ⎟ − 2 ⎜ ⎟ ⎥ .
⎝ r ⎠ ⎥⎦
⎢⎣⎝ r ⎠
Do the following:
a)
Calculate the value of r at which U ( r ) = 0 .
a)
b)
Calculate the value of r where U ( r ) is a minimum.
c)
d)
e)
Find the conservative force F . 
Calculate the value of r where F = 0 .
Sketch U ( r ) .

The potential energy is zero when
⎛r ⎞
U ( r ) = 0 → ⎜ o ⎟
⎝ r⎠
12
6
6
⎛r ⎞
⎛r ⎞
= 2 ⎜ o ⎟ → ⎜ o ⎟ = 2 ,
⎝r⎠
⎝ r⎠
(1)
and, therefore,
b)
A minimum value requires
dU (r )
⎛r ⎞
= 0 → 12 ⎜ o ⎟
⎝ r⎠
dr
11
ro
1/6
−1/ 6
= 2 → r = 2 ro .
r
(−r )
−2
⎛r ⎞
− 12 ⎜ o ⎟
⎝ r⎠
5
(−r )
−2
⎛r ⎞
= 0 → ⎜ o ⎟
⎝ r⎠
(2)
11
5
⎛r ⎞
= ⎜ o ⎟ . (3)
⎝ r⎠
This is true if and only if
c)
ro
= 1 → r = ro .
r
The conservative force is given by
S 10-38
(4)

d
d
−1
F = −r̂ U (r ) = − Uo ⎡ ro r
dr
dr ⎣
(
{
(
= − U o 12 ro r −1
12
) ( −r ) −12 ( r r
11
When F = 0 ,
11
−2
( ) ⎤⎦ r̂
) ( −r )} r̂
− 2 ro r
−1 5
o
U
= 12 2o
r
d)
)
−1 6
−2
⎧⎪⎛ ro ⎞ 11 ⎛ ro ⎞ 5 ⎫⎪
⎨⎜⎝ ⎟⎠ − ⎜⎝ ⎟⎠ ⎬ r̂ .
r ⎪⎭
⎪⎩ r
(5)
5
ro
⎛ ro ⎞
⎛ ro ⎞
=
→
= 1 → r = ro .
⎜⎝ r ⎟⎠
⎜⎝ r ⎟⎠
r
e)
(6)
U (r)
ro
r
−U o
10-51) The Yukawa potential energy function for the interaction of neutrons and protons in a
nucleus is given by
U ( r ) = − (ro / r )U o e − r /ro ,
(
)
where U o and ro are constants. Do the following:
a)
b)

Find the conservative force F .
−15
−12
Taking ro = 1.5 ×10 m and U o = 5 × 10 J , calculate:
i)
ii)
a)

F when r = ro ,

F when r = 3ro .
The force is given by

d
− ( r /r )
F = −r̂ Uo ⎡⎣ − ( ro / r ) e o ⎤⎦
dr
⎡ r − r /r ⎛ 1 ⎞
r ⎞⎤
⎡ 1 r ⎤ − r /r
− r /r ⎛
= Uo ⎢ o e ( o ) ⎜ − ⎟ + e ( o ) ⎜ − o2 ⎟ ⎥ r̂ = −U o ⎢ + o2 ⎥ e ( o ) r̂ .
⎝ r ⎠⎦
⎝ ro ⎠
⎣r r ⎦
⎣r
S 10-39
(1)
So,
b)

⎡ r + r ⎤ − (r /r )
F = −U o ⎢ o 2 ⎥ e o r̂ .
⎣ r ⎦
For the values given:
i)
r = ro :

⎡ r + r ⎤ − r /r
2U o −1
F = −U o ⎢ o 2 o ⎥ e ( o o ) r̂ = −
e r̂
r
r
⎣ o ⎦
o
−12
2 5 ×10 J −1
=−
e r̂ = − 2 , 450 N r̂ .
1.5 ×10 −15 m
ii)
r = 3ro :
(
(
)
)
⎡ r + 3r ⎤ − (3r / r )

4 U o −3
o
o o
F = −U o ⎢ o
⎥
e
r̂
=
−
e r̂
2
9 ro
⎢⎣ (3ro ) ⎥⎦
−12
4 5 ×10 J −3
=−
e r̂ = −74 N r̂ .
9 1.5 × 10−15 m
(
(
)
)
S 10-40
(2)
(3)
(4)