* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Can Fermat`s Principle accurately predict lens focusing? - TEM-EELS
Night vision device wikipedia , lookup
Ultraviolet–visible spectroscopy wikipedia , lookup
Birefringence wikipedia , lookup
Depth of field wikipedia , lookup
Fourier optics wikipedia , lookup
Anti-reflective coating wikipedia , lookup
Ray tracing (graphics) wikipedia , lookup
Schneider Kreuznach wikipedia , lookup
Image stabilization wikipedia , lookup
Retroreflector wikipedia , lookup
Lens (optics) wikipedia , lookup
Nonimaging optics wikipedia , lookup
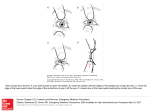
Can Fermat’s Principle accurately predict lens focusing? The focusing of a glass lens is usually described in terms of refraction at the air/glass and glass/air interfaces. An expression for the focal length fp of a biconvex lens, of thickness t at the optic axis and whose two spherical surfaces have the same radius of curvature R, can be obtained by applying Snell’s law, giving: 1/fp = (n-1)[2/R – (t /R2)(n-1)/n ] (1) Equation (1) is known as the Lensmaker’s Formula and its derivation involves small-angle approximations, meaning that fp is a paraxial focal length, only valid for rays that travel close to the optic axis. A thin-lens version of Eq.(1) is fp = (0.5)R /(n-1). The focusing power can be deduced much more quickly and with apparently no approximation by using Fermat’s Principle, according to which the time taken by light to travel between any two points is the smallest possible value. This least-time principle implies that if light can take two of more paths between the same two points, the travel time for these different paths must be identical. We can apply this principle to the biconvex lens, with an object point O at a distance u for the centre of the lens and image point I a distance v from the centre, as shown in Fig. 1. The simplest path (ray A) between O and I is a straight line (the optic axis) for which the travel time is: TA = (u – t/2)/c + nt/c + (v – t/2)/c = [(u + v + (n-1)t]/c (2) Figure 1. Fermat’s Principle applied to a glass lens of thickness t and radius r, whose two surfaces have a radius of curvature R . Rays A and B travel between object point O and image point I, ray C travels between point P and the focal point F. 2 Chapter Error! No text of specified style in document. A second path is represented by the ray B, which is refracted just inside the periphery of the lens, traveling through a negligible thickness of glass. The travel time is then: TB = (u2+r2)1/2/c + (v2+r2)1/2/c (3) The lens radius r is related to the lens thickness t and the radius of curvature R by basic geometry: r = Rsinφ, Rcosφ + t/2 = R, giving r2 = (t/2)(2R – t/2). Although path B involves a larger geometrical distance, light travels almost entirely in air (n=1) rather than slowing down by a factor n while traveling a distance t within the glass. Therefore the two travel times can be equal. First consider the symmetrical situation: u = v, giving magnification M = 1. Equating Eq.(2) and Eq.(3), Fermat’s principle gives the object and image distances as: u =v = 2r2/[2(n-1)t] – (n-1)t/8 = [(R – (t/4)(2+2n-n2)]/(n-1) (4) Increasing t in Eq. (4) corresponds to increasing the lens radius r and a larger deviation θ of the marginal ray B from the optic axis. The resulting object and image distances are shown in Table 1. For t = 1 (thin lens and a paraxial ray B), u and v are close to the value (2fp) predicted by the thin-lens equation: 1/u + 1/v = 1/fp, with fp given by the Lensmaker’s Formula. However Eq.(1) predicts a small decrease in the focusing power as the lens thickess increase, leading to an increase in fp and image distance, whereas Eq.(4) shows that the image distance decreases as r and the corresponding angle θ become larger. The discrepancy is almost proportional to the square of the angle θ of ray B (see last column of Table 1), suggesting spherical aberration. Table 1. Focal length f1 obtained by applying Fermat’s Principle to rays A and B in Fig.1, compared with a paraxial focal length fp obtained from the Lensmaker’s Formula. The lens radius of curvature R is taken as 100 units and other lengths are measured in the same units. t 1 10 20 r 9.99 31.2 43.6 θ 0.05 0.16 0.23 u=v 199.38 193.76 187.50 2 fp 200.4 203.4 207.0 (2fp – v)/θ2 191 189 186 The logic behind Fermat’s principle is the need for constructive interference between light rays that take slightly different paths, implying that the phase of an arriving wave remains unaltered, to first order. This requirement is met if the path length is a minimum or a maximum with respect to angular deviation of the ray. Fermat’s principle can be used to justify Snell’s law of refraction, the law of reflection (equal angles relative to the reflecting plane) and the fact that light travels in a straight line in a uniform medium. Recognizing that the final phase is the crucial quantity allows us to analyse the ray path C in Fig. 1, which starts from a point P that is on the same wavefront a point O and therefore has the same starting phase. The time taken for this ray to reach the focal point F is: Error! No text of specified style in document.. Error! No text of specified style in document. 3 TC = [u + (f 2 +r 2)1/2 ] / c (5) Setting TC equal to the time [(u + f + (n-1)t]/c taken for ray A to travel between O and F, the focal length is now: f0 = r2/[2(n-1)t] – (n-1)t/2 (6) which is slightly smaller than the value for path B. This situation relates more directly to the usual definition of spherical aberration, which assumes a parallel incident beam, allowing us to write the decrease in focal length as Δf = Csα2. Values of the spherical-aberration coefficient Cs are given in the last column of Table 2, and are about two thirds of the focal length of the lens. Table 2. Focal length f and aberration coefficient Cs deduced by applying Fermat’s Principle to rays A and C in Fig. A-1. The lens radius of curvature R is taken as 100 units. t 1 10 20 r 9.99 31.2 43.6 α 0.10 0.32 0.45 f0 99.5 95.0 90.0 ΔfD 1.66 16.25 31.73 fp 100.2 101.7 103.5 ΔfF 0.833 8.357 16.78 Cs 83.3 81.6 82.9 Based on standard geometric optics (Snell’s law), Drude [1] gives a formula for the focal shift ΔfD due to first-order spherical aberration (neglecting terms higher than α2), which for a symmetrical biconvex lens (lens parameter σ = -1) simplifies to: ΔfD = (r2/fp) (2 – n – 4n2 +4n3)/[8n(n – 1)2] (7) With R = 100 ~ fp, t = 1 and r ~ 10 , Eq.(7) gives ΔfD = fp –f0 = 1.66, as also stated in Drude’s table on p.56. Since r ~ 10 corresponds to α ~ 0.1 rad, the Drude value corresponds to Cs = Δf/α2 ~ 166 ~ 1.66 fp. Data from Glytsis [4] gives Cs ~ 1.55 fp, perhaps based on a slightly higher refractive index; changing n = 1.5 to n = 2.0 reduces ΔfD by more than a factor of 2. To compare with the value given by Fermat’s Principle, we must recognise that our Fermat image distances are measured relative to the mid-plane of the lens whereas a thick-lens image distance is measured relative to the rear principal plane. For a symmetrical biconvex lens, this plane is located a distance V from the vertex plane, where [3]: V = [(n-1)/n](fp/R)t = t/3 in the present case. The principal plane is therefore a distance t/2 – V = t/6 from the midplane and the Fermat focal distance f0 should be compared with t/6 +fp in order to compute the Fermat sphercial aberration: ΔfF = t/6 +fp – f0. As shown by the last two columns in Table 2, the Fermat values are about half of those predicted by Drude’s geometrical optics. Further problems arise if we consider a plano-convex lens. Fermat’s Principle (applied as in Fig.1) predicts exactly the same focal distance (measured relative to the flat surface of the lens) for the marginal ray C when the lens is reversed. The paraxial focal length (measured from the appropriate principal plane) is unchanged by reversing the lens but the principal planes are at x = +t and x = -2t/3 relative to the flat surface, if the refractive index is n = 1.5. Therefore the Fermat prediction is that the longitudinal spherical aberration will be higher by an amount 5t/3 when the front surface of the lens is planar. 4 Chapter Error! No text of specified style in document. If fp = 100, R = 50 for a plano-convex lens and r2 = 2Rt – t2, giving t ~ r2/(2R) = 1 for r = 10 but under these conditions Drude [2] gives ΔfD = 4.5 for planar front face and ΔfD = 1.17 for rear face plane, the spherical aberration being higher by 3.33 in the former case. The Fermat prediction of 5t/3 = 1.67 is again a factor of two smaller. One objection to using of rays that strike the edge of the lens (paths B and C in Fig. 1) might be that there is a discontinuity at the edge of the lens. However, these rays can be imagined to pass within a few wavelengths of the edge without substantially changing the equations. Moreover, Eq. (3) can be rewritten so that it applies to a ray travelling parallel to the optic axis within the lens (so that there is only one deflection, simplifying the algebra) at some arbitary distance h. The longitudinal spherical aberration scales proportional to α2 for all h and the image distance at h = r is identical to that given by Eq. (4). For a planoconvex lens with planar front surface, n = 1.5 and rear surface of radius R, Fermat’s Principle gives Cs = ΔfF/α2 = 4.5R = 2.25 fp,, once again half of Drude’s prediction. Is there a mistake in the logic or the algebra above? Can the optics books be wrong? Ray Egerton (July 2016) [email protected] References: [1] Paul Drude, The Theory of Optics (Dover, New York, 1959), page 54. [2] Paul Drude, The Theory of Optics (Dover, New York, 1959), table on page 56. [3] D.S. Goodman, Geometrical Optics, Eq. (204) on page 1.59. [4] E.N. Glytsis, http://users.ntua.gr/eglytsis/OptEng/Aberrations_p.pdf .