Download Mathematics 1448 Triangles: Proving Similarity: In

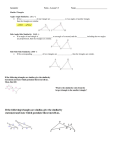
SAS® Curriculum Pathways®
Mathematics 1448
Triangles: Proving Similarity: In-class Worksheet
NAME(S):
CLASS:
DATE:
Review
► Suppose
ABC
XYZ. Complete the following statements:
1) Z 
2) Y 
3) X 
4) BC corresponds to
5) AC corresponds to
6) AB corresponds to
Demo: Understanding the Postulate and Theorems .............................................................
First, watch each demo in the Demo section of the Geometry Tool ON THE COMPUTER. Then, complete Problems
7 – 12.
7) The AA Similarity Postulate states that if two angles of one triangle are congruent to two angles of another
triangle, then _____________________________________________ .
8) Given the information
AB BC
and A  S, you cannot prove that

SF FG
ABC is similar to
SFG . Why not?
Hint: Draw and label the triangles.
9) True or False?
If
AB BC CA


, then
TR RY YT
10) True or False?
If
AB CA
and A  J, then

IK
KJ
ABC
11) Complete the statement of proportions that demonstrates
TRY by the SSS Similarity Theorem.
ABC
PMX
IKJ by the SAS Similarity Theorem.
HGJ by the SSS Similarity Theorem.
PM


HG HJ
12) If you know all the angle and side measures of RWM , how many angle measures must you know
of GED in order to prove the two triangles similar?
Copyright © 2011, SAS Institute Inc., Cary, NC, USA, All Rights Reserved
3/1/2011
Page 1 of 4
SAS® Curriculum Pathways®
Mathematics 1448
Triangles: Proving Similarity: In-class Worksheet
Practice: Applying the Concepts ................................................................................................
The Practice section of the Geometry Tool provides you with a chance to create and view two similar triangles
using the similarity postulate and theorems.
Use the Practice section ON THE COMPUTER to walk through the Example Problem. The Example Problem will
familiarize you with the interactive parts of the Practice section and provide direction for completing
Problems 13 – 17 on this worksheet.
Example Problem
Given:
First Triangle:
A
ABC
PQR by SAS
Scale Ratio: 1 to 2
B
C
Step 1: Create similar triangles.
a)
Create
ABC on the computer in a shape similar to the triangle given on the worksheet.
For this example, use the default triangle provided on the computer.
For other problems, you may click and drag the vertices of the first triangle to any size and
shape. However, if you accidentally change it for this example problem, click RESET at the
bottom of the window.
b)
Use the similarity statement from the worksheet to
complete the similarity statement on the computer:
c)
Select the sides or angles that are necessary to prove the two triangles are similar by the
postulate or theorem in the Similarity Statement.
For this example, use the angle and sides shown to the right.
d)
Calculate the measures needed to create similar triangles according to the scale ratio
given on the worksheet.
For this example, enter the measures shown to the right to achieve a scale ratio of 1 to 2.
Hint: For other problems, you may want to adjust your first triangle to make it easier to calculate the measures of the
second triangle.
e)
Click
f)
Enter the scale ratio from the worksheet into the Scale Ratio fields on the computer.
(optional) to display the second triangle.
Step 2: Check your answers.
g)
Check for similar triangles by clicking
in the Create Similar Triangles panel.
h)
Check your scale ratio by clicking
i)
Adjust your answers and recheck as necessary.
beside the scale ratio fields.
Step 3: View and record your answers.
j)
Click
k)
Sketch the second triangle on the worksheet. Approximate the relative size of the triangles.
l)
Label only the parts of the triangles that apply to the postulate or theorem selected.
Note: Click
triangles.
to view the triangles in relation to one another.
at the bottom left of the window to show and hide the measures on the two similar
See the completed Example problem on the next page.
Copyright © 2011, SAS Institute Inc., Cary, NC, USA, All Rights Reserved
3/1/2011
Page 2 of 4
SAS® Curriculum Pathways®
Mathematics 1448
Triangles: Proving Similarity: In-class Worksheet
► Use the Geometry Tool and directions from the Example problem on the previous page to complete Problems
13 – 17.
Given
Ex.
Similar Triangles To Scale
Q
First Triangle:
B
A
PQR by SAS
ABC
3
53º
B
C
A
Scale Ratio: 1 to 2
13)
R
C
5
6
10
53º
P
First Triangle:
B
C
A
RST by SSS
ABC
Scale Ratio: 1 to 5
14)
First Triangle:
B
C
A
PET by SAS
ABC
Scale Ratio: 1 to 3
15)
First Triangle:
B
C
A
ABC
ETP by SAS
Scale Ratio: 1 to 4
16)
First Triangle:
B
C
A
ABC
JFM by SSS
Scale Ratio: 2 to 1
17)
First Triangle:
B
A
C
ABC
XYZ by AA
Scale Ratio: 10 to 1
Copyright © 2011, SAS Institute Inc., Cary, NC, USA, All Rights Reserved
3/1/2011
Page 3 of 4
Mathematics 1448
SAS® Curriculum Pathways®
Triangles: Proving Similarity: In-class Worksheet
Proof: Extending the Reasoning .................................................................................................
First, complete the proof in the Proof section of the Geometry Tool ON THE COMPUTER. Then, answer these questions.
18) In Step 1 of the online proof, what postulate supports drawing a line through a point parallel to another line?
19) What property of equality is used?
20) Name the two postulates (one similarity, one congruence) that were used in this proof to prove the SAS
similarity theorem.
Copyright © 2011, SAS Institute Inc., Cary, NC, USA, All Rights Reserved
3/1/2011
Page 4 of 4