Download SAS and SSS Similarity Practice - Sulkes

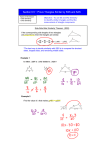
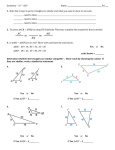
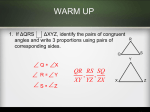
Name: ___________________________________
February 19th, 2013
Geometry, Mrs. Sulkes
7-5 SAS
and SSS
Theorems (Proofs and Practice)
SAS Similarity Theorem: (SAS ) If an angle of one triangle is congruent to an angle of
another triangle and the sides including those angles are in proportion, then the triangles are
similar.
A
D
B
C
E
F
Given:
Prove:
Statements
1.
Reasons
1. given
2. Draw point X on DE such in that DX=AB
2.
3. Draw a line through X and parallel to EF
4. Draw point Y, the intersection of the line
3.
4.
and DF .
Example:
KI
JI

HI GI
Prove: KJ  HI  HG  KI
Given:
J
K
I
G
H
SSS Similarity Theorem: (SSS
then the triangles are similar.
) If the corresponding sides of two triangles are in proportion,
A
D
B
C
E
Given:
Prove:
F
Example
Given: Equilateral triangles ABC and DEF
Prove: ABC ~ DEF
Example:
NP QN
PQ


NM ON MO
Prove: M  QPN
Given:
O
Q
M
P
N