* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 02_One compartment IV Bolus
Discovery and development of cyclooxygenase 2 inhibitors wikipedia , lookup
Compounding wikipedia , lookup
Pharmacognosy wikipedia , lookup
Pharmacogenomics wikipedia , lookup
Neuropharmacology wikipedia , lookup
Pharmaceutical industry wikipedia , lookup
List of comic book drugs wikipedia , lookup
Prescription costs wikipedia , lookup
Prescription drug prices in the United States wikipedia , lookup
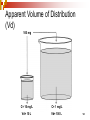
Drug discovery wikipedia , lookup
Drug design wikipedia , lookup
Drug interaction wikipedia , lookup
Theralizumab wikipedia , lookup
One Compartment Open Model IV bolus Dr Mohammad Issa 1 One compartment 2 More than one compartment 3 One compartment open model The one-compartment open model offers the simplest way to describe the process of drug distribution and elimination in the body. This model assumes that the drug can enter or leave the body (ie, the model is "open"), and the body acts like a single, uniform compartment. The simplest route of drug administration from a modeling perspective is a rapid intravenous injection (IV bolus). 4 One compartment open model The simplest kinetic model that describes drug disposition in the body is to consider that the drug is injected all at once into a box, or compartment, and that the drug distributes instantaneously and homogenously throughout the compartment. Drug elimination also occurs from the compartment immediately after injection. 5 One compartment: 6 Properties of a Pharmacokinetic Compartment 1. Kinetic homogeneity. A compartment contains tissues that can be grouped according to similar kinetic properties to the drug allowing for rapid distribution between tissues 2. Although tissues within a compartment are kinetically homogeneous, drug concentrations within a compartment may have different concentrations of drug depending on the partitioning and binding properties of the drug. 3. Within each compartment, distribution is immediate and rapidly reversible. 4. Compartments are interconnected by first-order rate constants. Input rate constants may be zero order 7 One compartment: IV bolus administration (dose = X0) Drug amount in the Body (X) Elimination process Elimination rate constant (K) Based on the assumption of first order elimination process: eliminatio n rate K X 8 One compartment open model Drug Conc (C) D K t C e Vd Time C= concentration D= dose Vd: Volume of distribution K: elimination rate constant t: time 9 How to distinguish one comp? log (C) Plotting log(C) vs. time yields a straight line Time 10 Fundamental parameters in one compartment Apparent Volume of Distribution (Vd) Elimination rate constant (K) Elimination half life (t1/2) Clearance (Cl) 11 Apparent Volume of Distribution (Vd) 100 mg C= 10 mg/L C= 1 mg/L Vd= 10 L Vd= 100 L 12 Apparent Volume of Distribution (Vd) In general, drug equilibrates rapidly in the body. When plasma or any other biologic compartment is sampled and analyzed for drug content, the results are usually reported in units of concentration instead of amount Each individual tissue in the body may contain a different concentration of drug due to differences in drug affinity for that tissue. Therefore, the amount of drug in a given location can be related to its concentration by a proportionality constant that reflects the volume of fluid the drug is dissolved in The volume of distribution represents a volume that must be considered in estimating the amount of drug in the body from the concentration of drug found in the 13 sampling compartment The real Volume of Distribution has physiological meaning and is related to body water Total body water 42 L Plasma Interstitial fluid Intracellular fluid Plasma volume 4 L Interstitial fluid volume 10 L Intracellular fluid volume 28 L 14 Apparent Volume of Distribution Drugs which binds selectively to plasma proteins, e.g. Warfarin have apparent volume of distribution smaller than their real volume of distribution Drugs which binds selectively to extravascular tissues, e.g. Chloroquines have apparent volume of distribution larger than their real volume of distribution. The Vd of such drugs is always greater than 42 L (Total body water) 15 Apparent Volume of Distribution Lipid solubility of drug Degree of plasma protein binding Affinity for different tissue proteins Fat : lean body mass Disease like Congestive Heart Failure (CHF), uremia, cirrhosis 16 Apparent Volume of Distribution In general, drug equilibrates rapidly in the body. When plasma or any other biologic compartment is sampled and analyzed for drug content, the results are usually reported in units of concentration instead of amount Each individual tissue in the body may contain a different concentration of drug due to differences in drug affinity for that tissue. Therefore, the amount of drug in a given location can be related to its concentration by a proportionality constant that reflects the volume of fluid the drug is dissolved in The volume of distribution represents a volume that must be considered in estimating the amount of drug in the body from the concentration of drug found in the 17 sampling compartment Apparent Volume of Distribution: Mathematics In order to determine the apparent volume of distribution of a drug, it is necessary to have plasma/serum concentration versus time data X0 dose Vd initial conc. C0 18 Apparent volume of distribution estimation 1. Plot log(C) vs. time 2. Plot the best-fit line 3. Extrapolate to the Y-axis intercept (to estimate initial concentration, C0) 4. Estimate Vd: X0 dose Vd initial conc. C0 19 1- Plot log(C) vs. time 7 Log (Conc) 6.8 6.6 6.4 6.2 6 5.8 0 1 2 3 4 5 6 Time 20 2- Plot the best-fit line 7 Log (Conc) 6.8 6.6 6.4 6.2 6 5.8 0 1 2 3 4 5 6 Time 21 3-Extrapolate to the Y-axis intercept (to estimate C0) 7 Log (Conc) 6.8 6.6 6.4 C0 6.2 6 5.8 0 1 2 3 4 5 6 Time 22 4-Estimate Vd 7 X0 dose Vd initial conc. C0 Log (Conc) 6.8 6.6 6.4 Log(C0) 6.2 6 5.8 0 1 2 3 4 5 6 Time 23 The Extent of Distribution and Vd in a 70 kg Normal Man Vd, L % Body Weight Extent of Distribution 5 7 Only in plasma 5-20 7-28 In extracellular fluids 20-40 28-56 In total body fluids. >56 In deep tissues; bound to peripheral tissues >40 24 Elimination rate constant (K) Elimination rate constant represents the fraction of drug removed per unit of time K has a unit of reciprocal of time (e.g. minute-1, hour-1, and day-1) With first-order elimination, the rate of elimination is directly proportional to the serum drug concentration 25 Elimination rate constant estimation 1. Plot log(C) vs. time 2. Plot the best-fit line 3. Calculate the slope using two points on the best-fit line Estimate K: K Slope 2.303 4. 26 1- Plot log(C) vs. time 6.8 6.7 Log (Conc) 6.6 6.5 6.4 6.3 6.2 6.1 6 0 1 2 3 4 5 6 Time 27 2- Plot the best-fit line 6.8 6.7 Log (Conc) 6.6 6.5 6.4 6.3 6.2 6.1 6 0 1 2 3 4 5 6 Time 28 3- Calculate the slope using two points on the best-fit lin 6.8 log( C1 ) log( C2 ) Slope t1 t 2 6.7 Log (Conc) 6.6 6.5 6.4 (Log(C1), t1) 6.3 6.2 (Log(C2), t2) 6.1 6 0 1 2 3 4 5 6 Time 29 4- Estimate K 6.8 K Slope 2.303 6.7 Log (Conc) 6.6 6.5 6.4 6.3 6.2 6.1 6 0 1 2 3 4 5 6 Time 30 Elimination half life (t1/2) The elimination half life is sometimes called ‘‘biological half-life’’ of a drug The elimination half life is defined as the time (h, min, day, etc.) at which the mass (or amount) of unchanged drug becomes half (or 50%) of the initial mass of drug 31 Elimination half life (t1/2) estimation Two methods: From the value of K: t1/ 2 Directly 0.693 K from Conc vs. time plot Select a concentration on the best fit line (C1) Look for the time that is needed to get to 50% of C1 half-life 32 Clearance (Cl) Clearance is a measure of the removal of drug from the body Plasma drug concentrations are affected by the rate at which drug is administered, the volume in which it distributes, and its clearance A drug’s clearance and the volume of distribution determine its half life 33 Clearance (Cl) Clearance (expressed as volume/time) describes the removal of drug from a volume of plasma in a given unit of time (drug loss from the body) Clearance does not indicate the amount of drug being removed. It indicates the volume of plasma (or blood) from which the drug is completely removed, or cleared, in a given time period. Figures in the following two slides represent two ways of thinking about drug clearance: In the first Figure, the amount of drug (the number of dots) decreases but fills the same volume, resulting in a lower concentration Another way of viewing the same decrease would be to calculate the volume that would be drug-free if the concentration were held constant as resented in the 34 second Figure Clearance (Cl) the amount of drug (the number of dots) decreases but fills the same volume, resulting in a lower concentration 35 Clearance (Cl) 36 Clearance (Cl) The most general definition of clearance is that it is ‘‘a proportionality constant describing the relationship between a substance’s rate of elimination (amount per unit time) at a given time and its corresponding concentration in an appropriate fluid at that time.’’ Clearance can also be defined as ‘‘the hypothetical volume of blood (plasma or serum) or other biological fluids from which the drug is totally and irreversibly removed per unit time.’’ 37 Clearance (Cl) estimation For ALL LINEAR pharmacokinetics (including one compartment) , clearance is calculated using: dose Cl AUC where AUC is the area under the concentration curve (it will be discussed later) 38 Clearance (Cl) estimation For One compartment pharmacokinetics , clearance is calculated using: Cl K Vd 39 Clearance (Cl) Drugs can be cleared from the body by different pathways, or organs, including hepatic biotransformation and renal and biliary excretion. Total body clearance of a drug is the sum of all the clearances by various mechanisms. Clt Clr Clh Clother (Cl t , Clr and Clh total, renal, and hepatic Cl) 40 Elimination rate The elimination rate at any time can be calculated using: Elimination rate = K*X(t) OR Elimination rate = Cl*C(t) where X(t) is the amount of drug in the body at time t, C(t) is the concntration of drug at time t 41 Area Under the Conc. Time Curve (AUC) calculation Two methods: Model dependent: can be used only for one compartment IV bolus Model independent: Can be used for any drug with any route of administration 42 AUC calculation: Model dependent With one compartment model, first-order elimination, and intravenous drug administration, the AUC can be calculated using: Dose C0 AUC K Vd K 43 AUC calculation: Model independent 1200 1000 800 600 400 200 0 0 2 4 6 8 10 12 44 AUC calculation: Model independent 1200 1- Divide the area into different parts based on the observed concentration points (parts 1-5) 1000 800 600 1 400 2 200 3 4 5 0 0 2 4 6 8 10 12 45 AUC calculation: Model independent 1200 2- Calculate the area for each part of the parts 1,2,3 and 4 (until the last observed concentration) using trapezoidal rule 1000 800 600 1 400 2 200 3 4 5 0 0 2 4 6 8 10 12 46 Trapezoidal rule (Trapezoid = )شبه المنحرف C1 C2 C 2 C1 area (t 2 t1 ) 2 where C = concentration t = time t1 t2 47 AUC calculation: Model independent 3- For part 5 (area between the last observed concentration and infinity) use the following equation: C* C* area K 48 AUC calculation: Model independent 1200 4- The total AUC (from zero to infinity) is the sum of the areas of parts: 1,2,3,4, and 5 1000 AUC 0 AUC1 AUC 2 AUC 3 AUC 4 AUC 5 800 600 1 400 2 200 3 4 5 0 0 2 4 6 8 10 12 49 Fraction of the dose remaining Fraction of dose remainig (F = X(t)/X0) is given by the following equation: K t Amount at time t X 0 e F dose X0 e K t since t1/2= 0.693/k, the equation can be represented as: t t 0.693 1 t1 / 2 t1 / 2 Fe 2 50 Time to get to certain conc. Time to get to certain concentration (C*) is given by: C* C 0 e K t e C0 K t ln C * C0 ln C * t K K t C0 C* 51 Applications of one compartment model Case 1: Predicting Plasma Concentrations Case 2: Duration of Action Case 3:Value of a Dose to Give a Desired Initial Plasma Concentration 52 Case 1: Predicting Plasma Concentrations A 20-mg dose of a drug was administered as an intravenous bolus injection. The drug has the following pharmacokinetic parameters: k = 0.1 h−1 and Vd = 20 L Calculate the initial concentration (C0 ) 2. Calculate the plasma concentration at 3 h 1. 53 Case 1: Predicting Plasma Concentrations 1. Calculate the initial concentration (C0 ) dose 20 mg C0 1 mg/L Vd 20 L 2. Calculate the plasma conc. at 3 h C C0 e K t 1 e -(0.1)(3) 0.74 mg/L 54 Case 2: Duration of Action The duration of action of a drug may be considered to be the length of time the plasma concentration spends above the MEC. Its determination is best illustrated by example 2. 55 Case 2: Duration of Action Continuing with the drug used in Example 1, if the therapeutic range is between 5 and 0.3 mg/L, how long are the plasma concentrations in the therapeutic range? 56 Case 2: Duration of Action As indicated in the diagram (previous slide) C0 =1 mg/L. Thus, at time zero the plasma concentration is in the therapeutic range. The plasma concentration will remain therapeutic until it falls to the MEC (0.3 mg/L). At what time does this occur? C0 ln C * t K 1 ln / 0.1 12.0 hr 0.3 57 Case 3: Value of a Dose to Give a Desired Initial Plasma Concentration Continuing with the drug used in Examples 1 and 2, If the initial Cp of 1 mg/L is unsatisfactory, Calculate a dose to provide an initial plasma concentration of 5 mg/L. dose dose C0 Vd C0 Vd mg dose 5 20 L 100 mg L 58 Examples 59 Example 1 Ten mg metoclopramide was administered intravenously to a 72 kg patient. The minimum plasma concentration required to cause significant enhancement of gastric emptying is 50 ng/mL. The following plasma concentrations were observed after analysis of the specimen. 60 Example 1 Time (hr) Conc. (ng/ml) 1 90.0 2 68.0 4 40.0 6 21.5 8 12.0 10 7.0 61 Example 1 Calculate the biological half-life of the drug elimination (t½), the overall elimination rate constant (K), the volume (Vd), the coefficient of distribution and the duration of action (td) 62 Example 1 2.5 2 log (Conc) y = -0.1243x + 2.0832 R2 = 0.9995 1.5 1 0.5 0 0 2 4 6 time (hr) 8 10 12 63 Example 1 The elimination rate constant can be obtained from the slope: K Slope 2.303 (0.1243) (2.303) 0.286 hr 1 Another way to calculate the slope is using: log(C1) - log(C2) Slope t1 - t2 64 Example 1 Another way to calculate the slope (if you do not have the ability to do regression) is using: log(C1) - log(C2) Slope t1 - t2 where (C1,t1) and (C2,t2) are two different conc. time points It is important to note that the first method for calculating the slope is more accurate 65 Example 1 Calculating the slope using the second method: log(40) - log(21.5) Slope -0.13481 4-6 Note that the value of the slope is similar to the value estimated using the first method (-0.1243) 66 Example 1 the biological half-life of the drug elimination (t½): t 0.5 0.693 0.693 2.42 hr K 0.286 The volume of distribution (Vd): dose 10 10 Vd 2.0832 C0 10 121.12 mg 10 6 ng L 0.083 3 83 L ng/ml mg 10 ml 67 Example 1 Intercept = log (C0) C0= 10intecept 2.5 2 log (Conc) y = -0.1243x + 2.0832 R2 = 0.9995 1.5 1 y = -0.1243x + 2.0832 R2 = 0.9995 0.5 0 0 2 4 6 time (hr) 8 10 12 68 Example 1 the coefficient of distribution = Vd/wt =83 L/ 72 kg= 1.15 L/kg the duration of action (td). td is the time needed for the conc. To get to 50 ng/ml : C0 ln C * t K 121.12 ln 50 0.286 3.1 hr 69 Example 2 An adult male patient was given the first dose of an antibiotic at 6:00 AM. At 12:00 noon the plasma level of the drug was measured and reported as 5 µg/ml. The drug is known to follow the one compartment model with a half-life of 6 hours. The recommended dosage regimen of this drug is 250 mg q.i.d. the minimum inhibitory concentration is 3 µg/ml. Calculate the following: Apparent volume of distribution Expected plasma concentration at 10 AM. Duration of action of the first dose Total body clearance Fraction of the dose in the body 5 hours after the injection Total amount in the body 5 hours after the injection Cumulative amount eliminated 5 hours after the injection Total amount in the body immediately after injection of a second dose at 12:00 noon Duration of action of first dose only if dose administered at 6:00 AM was 500 70 mg. Example 2 Elimination K 0.693 Initial rate constant: t 0.5 0.693 0.116 hr 1 6 concentration: The conc. at 12:00 noon (6 hrs after the first dose) is 5 µg/ml: C (t 5) C0 e k t C (t 5) 5 C0 0.1166 10 ug/ml k t e e 71 Example 2 Apparent volume of distribution: C(t=6hrs)= 5 ug/ml. Since the half life is 6 hrs, C0 = 10 ug/ml. X0 VD C0 250 mg 25000 ml 25 L -3 μg 10 mg 10 ml μg Expected plasma concentration at 10 AM K 0.693 /t 0.5 0.693 / 6 0.1155 hr -1 C(t 4) C0 e K t 6.3 μg/ml 72 Example 2 Duration of action of the first dose C ln 0 t C * K 10 ln 3 0.1155 10.42 hr Total body clearance Cl K VD 2.89 L/hr Fraction of the dose in the body 5 hours after the injection 5 1 6 F 0.56 2 73 Example 2 Total amount in the body 5 hours after the injection = (0.56)(250 mg) = 140 mg Cumulative amount eliminated 5 hours after the injection = dose – amount in the body = 250 – 140 = 110 mg Total amount in the body immediately after injection of a second dose at 12:00 noon Total amount = amount from the first dose + amount from the second dose = 125 + 250 = 375 mg 74 Example 2 Duration of action of first dose only if dose administered at 6:00 AM was 500 mg t d 10.42 hr 6 hr 16.42 hrs Note that 6 hrs (one t0.5) is needed for the amount in the body to decline from 500 mg to 250 mg 75 Example 3 The therapeutic range of a drug is 20-200 mg/L. After an intravenous bolus injection of 1.0 gm followed by regression analysis of the concentration of the drug in plasma (in units of mg/L) versus time (in hours), the following linear equation was obtained log Cp 2 0.1t Calculate the following Duration of action Total body clearance Rate of elimination at 2 hours 76 Example 3 From the equation: log Cp 2 0.1t log( C0 ) slope t The following were estimated: C0 10 2 100 mg/L K Slope 2.303 (0.1) (2.303) 0.23 hr 1 VD X 0 1000 mg 10 L C 0 100 mg/L 77 Example 3 Duration of action: C ln 0 td C * K 100 ln 20 0.23 7 hr Total body clearance= K∙Vd=(0.23)(10) =2.3 L/hr Rate of elimination at 2 hours: Elimination rate = Cl*C(t=2) = 2.3*63 =145 mg/hr log(Cp(t 2)) 2 (0.1)(2) 1.8 Cp(t 2) 101.8 63 mg/L 78 79