Download Experiment 6 ~ Joule Heating of a Resistor

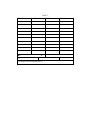
Experiment 6 ~ Joule Heating of a Resistor
Introduction:
The power P absorbed in an electrical resistor of resistance R, current I, and voltage V is given
by P = I2R = V2/R = VI. Despite the fact that it has units of power, it is commonly referred to as
joule heat. A given amount of electrical energy absorbed in the resistor (in units of joules)
produces a fixed amount of heat (in units of calories). The constant ratio between the two has the
value 4.184 J/cal and is numerically equivalent to the specific heat capacity of water. In this lab,
an electric coil will be immersed in water in a calorimeter, and a known amount of electrical
energy will be input to the coil. Measurements of the heat produced will be used to accomplish
the following objectives:
1. Demonstrate that the rise in temperature of the system is proportional to the electrical energy
input.
2. Determination of an experimental value for J and comparison of that value with the known
value.
Theory:
When a resistor of resistance R has a current I at voltage V, the power absorbed in the resistor is
P = I2R = V2/R = VI
(1)
Power is energy per unit time, and if the power is constant, the energy U delivered in time t is
given by:
U = Pt
(2)
Substituting equation 1 into equation 2 gives the following expression for the electrical energy:
U = VIt
(3)
When a resistor absorbs electrical energy, it dissipates this energy in the form of heat Q. If the
resistor is placed in the calorimeter, the amount of heat produced can be measured when it is
absorbed in the calorimeter. Consider the experimental arrangement shown in Figure 5.1, which
a resistor coil (also called and “immersion heater”) is immersed in the water in a calorimeter.
The heat Q produced in the resister is absorbed by the water, calorimeter cup, and the resistor
coil itself. This heat Q produces a rise in temperature ΔT. The heat Q is related to ΔT. The heat
Q is related to ΔT by:
Q = (mwcw + mccc + mrcr) ΔT
(4)
The mc’s are the masses and specific heats of the water, the calorimeter, and the resistor. Let mc
stand for the sum of the product of the mass and the specific heat for the three objects that absorb
the heat. In those terms the heat Q is given by the following:
Q = mcΔT
(5)
The electrical energy absorbed in the resistor is completely converted to heat. The equality of
those two energies is expressed as
U (J) = J (J/cal) Q (cal)
(6)
J represents the conversion factor from joules to calories. Using the expression for U and Q from
equations 3 and 5 in equation 6 leads to
VIt(J) = J(J/cal) mcΔT(cal)
(7)
Figure 1: Experimental arrangement and circuit diagram for the calorimetric
measurement of the heat produced in an immersion heater by an electrical current.
Suppose that a fixed current and voltage are applied to the resistor in a calorimeter, and the
temperature rise ΔT is measured as a measured as a function of the time t. Equation 7 predicts
that a graph with VIt(J) as the y-axis and mcΔT(cal) as the x-axis should produce a straight line
with J as the slope.
Equipment:
Immersion heater coil to fit standard calorimeter
Calorimeter and thermometer
Direct-current power supply (0.5 A)
Ammeter (0-5 A), Voltmeter (0-10V)
Laboratory timer
Laboratory balance
Procedure:
The procedure outlined below is designed to also use Data Studio with a thermometer
attached. The program will take continuous measurements and store the data in a table
with the time. You may save the data and analyze it using Excel. For this part of the lab you
will use the laptop connected to your set up. Save the Data Studio file to the desktop. You will
have to change the file formate to all files and save as a .ds file. The file can be downloaded from
the Physics lab site at:
http://www.umsl.edu/~physics/lab/electricitylab/12-lab6.html.
Once you have the laptop on and the sensors plugged in you can double click on the saved file to
open the Data Studio program. If you need to find it later the program can be found in the
‘Education’ folder under the programs in the start menu. To start taking measurements, click on
the run button on the upper tool bar. The lab TA will provide more instruction. If you make a
mistake with the program you can start over by closing the program without saving and opening
it again from the Desktop.
An empty graph should appear; to start the measurement press the green ‘play’ button at the top
of the screen. To stop the measurement press the ‘stop button’ (the same button).
Determine the mass mc of the calorimeter cup and record it in the Data Table. You may neglect
the mass of the resistor coil since the quantity mrcr∆T is a very small fraction of the total Q in
equation 4.
Place enough water (about 150-200 mL) in the calorimeter cup to immerse the resistor coil
completely. The water temperature should be a few degrees below room temperature. Be sure
that the coil is completely covered by the water, but do not use any more water than is necessary.
Determine the mass of the water plus the calorimeter cup and record it in the Data Table.
Determine the mass of the water by subtraction and record it as mw in the Data Table.
Place the immersion heater in the calorimeter cup and construct the circuit shown in Figure 5.1.
Check again that the immersion heat is below the water level. If it is not, add some more water
and determine the mass of the water again.
Turn on the power supply and adjust the current to .5 A. Do this quickly and then turn off the
supply with the output level still adjusted to the setting that produced the desired current. Do not
allow the supply to stay on long enough to appreciably heat the water. Stir the system several
minutes to allow it to come to equilibrium.
Determine the initial temperature Ti and record it in the Data Table. Estimate the thermometer
readings to the nearest 0.1°C for all temperature measurements.
With the power supply still set to the output level required to produce 0.5 A, turn on the power
supply and simultaneously start the laboratory timer. Record the initial values of the current I and
the voltage V in the Data Table. Let the timer run continuously and stir the system often.
Measure and record the temperature T, the current I, and the Voltage V every 60 s for 8 minutes.
Record all data in the Data Table.
Calculations:
Calculate the quantity mc, where mc = mwcw + mccc and record it in the Calculations Table.
Calculate the temperature rise of ΔT above the initial temperature Ti from ΔT = T – Ti for each
of the measured values of T and record the results in the Calculations Table.
Calculate the quantity mcΔT for each case and record the results in the Calculations table.
For each measurement of the voltage V and current I calculate the product VI and record the
results in the Calculations Table.
Calculate the mean and standard deviation σVI for the values of VI and record the results in the
calculations Table.
Calculate the quantity for each time t and record the results in the Calculations Table.
Perform a linear least squares fit to the data with as the y-axis and mcΔT as the x-axis.
Determine the slope Jexp, the intercept A, and the correlation coefficient R and record them in the
Calculations Table.
Calculate the percentage error in the value of Jexp compared to the known value of J = 4.184
J/cal.
Graphs:
Graph the data with VIt as the ordinate (y-axis) and mcΔT as the abscissa (x-axis). Also show on
the graph the straight line obtained from the linear least squares fit.
Table 1
Mass Calorimeter =
g
Mass Calorimeter + Mass Water =
g
Mass Water =
t(s)
g
V (V)
Ti =
°C
c for calorimeter =
cal/(g °C)
c for water =
cal/(g °C)
I(A)
T(°C)
0
60
120
180
240
300
360
420
480
mc = mwcw + mccc= ______________(cal/°C)
Table 2
ΔT(°C)
mcΔT (cal)
0
0
=
Jexp =
J/cal
VI (W)
VI t (J)
0
W
A=
Percentage error in experimental J =
σVI =
W
J
R=
Questions:
When the electrical power input is approximately constant, the temperature rise of the system
should be proportional to the elapsed time. Does your data confirm this expectation? State the
evidence for your answer.
What is accuracy of your experiment value for J?
Does the correlation coefficient of the least squares fit to the data indicate strong evidence for
linearity in this data?
How long from the original starting time would it have taken to achieve a temperature of 50.0°C
with the experimental arrangement you used? Show your work.
Assuming that one used the same heating coil and that its resistance did not change, how much
would the power be increased if the voltage were increased by 50%? Show your work.
Suppose that some liquid other than water were used in the calorimeter. If the liquid had a
specific heat of 0.25 cal/g-°C, would that tend to improve the results, make them worse, or have
no effect on them? Explain clearly the reasoning behind your answer.