* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Modal_Logics_Eyal_Ariel_151107
Axiom of reducibility wikipedia , lookup
Dynamic logic (modal logic) wikipedia , lookup
Truth-bearer wikipedia , lookup
Meaning (philosophy of language) wikipedia , lookup
Model theory wikipedia , lookup
History of the function concept wikipedia , lookup
Foundations of mathematics wikipedia , lookup
Abductive reasoning wikipedia , lookup
Willard Van Orman Quine wikipedia , lookup
Fuzzy logic wikipedia , lookup
Lorenzo Peña wikipedia , lookup
Structure (mathematical logic) wikipedia , lookup
Sequent calculus wikipedia , lookup
Propositional formula wikipedia , lookup
Saul Kripke wikipedia , lookup
Jesús Mosterín wikipedia , lookup
First-order logic wikipedia , lookup
Combinatory logic wikipedia , lookup
History of logic wikipedia , lookup
Mathematical logic wikipedia , lookup
Quantum logic wikipedia , lookup
Natural deduction wikipedia , lookup
Law of thought wikipedia , lookup
Curry–Howard correspondence wikipedia , lookup
Propositional calculus wikipedia , lookup
Laws of Form wikipedia , lookup
Intuitionistic logic wikipedia , lookup
Ariel Jarovsky and Eyal Altshuler
8/11/07, 15/11/07
1
Today
• A short review
• Multi-Modal Logic
• First Order Modal Logic
• Applications of Modal Logic:
• Artificial Intelligence
• Program Verification
• Summary
2
3
Introduction
Modal Logics are logics of qualified truth.
(From the dictionary)
Modal – of form, of manner, pertaining to
mood, pertaining to mode
Necessary, Obligatory, true after an action,
known, believed, provable, from now on,
since, until, and many more…
4
Syntax – Language
The formal language:
A non-empty set of propositions (as in
classical logic): P { p , p , p , }
1
2
3
{¬, Ù, Ú, , , ,W,, à }
Operators:
Parentheses.
Some define the ◊ as:
The Modal
Operators
à A def ¬W¬A
5
Syntax – Formulas
• Formulas are the only syntactic category of
Propositional Modal Logics, as in CPL.
• Every proposition p is a formula.
• If A, B are formulas, then the following are also
formulas:
•
¬A,
A Ù B,
A Ú B,
A B,
AB
• If A is a formula then the following are also
formulas:
•
WA
àA
6
Modal Logics - Semantics
Possible worlds semantics
(Kripke, 1959)
The different possible worlds represent
the states of a given problem.
7
Semantics - Frame
A frame is a pair (W,R) where W is a non-
empty set and R is a binary relation on W.
W is the set of all possible worlds, or states.
R determines which worlds are accessible
from any given world in W.
We say that b is accessible from a iff (a,b)R.
R is known as the accessibility relation.
8
Semantics – Model
A Model is a triple M=(W,R,V) while (W,R) is a
frame and V is a valuation.
A valuation is a function V : P W {T , F }.
Informally, V(p,w)=T is to be thought as p is
true at world w.
9
Semantics – Semantic Relation
The relation
‘
between a pair (M,w) where
M is a model and w is a world, and a formula
A, is defined recursively as follows:
M , w ‘ p, p P V ( p, w) T
M , w ‘ pA Ù B M , w ‘ A and M , w ‘ B
Similar for the other classical logic connectors.
M , w ‘ WA x W if wRx then M , x ‘ A
M , w ‘ à A x W s.t. wRx Ù M , x ‘ A
10
Logics
Given a language L(P) (P is a set of atoms) a
logic is defined to be any subset of formulas
generated from P that satisfies:
includes all tautologies;
Closure under Modus Ponens.
Closure under uniform substitution.
11
Normal Logic
A logic is said to be normal if it contains the
formula scheme:
K : W( A B) (WA WB)
and if it is provided with the modal
inference necessitation rule:
Λ A
Λ WA
12
Axiomatic Systems
An axiomatic system for a normal logic is
made up of the following three components:
An axiomatic system of CPL (as HPC)
The axiom scheme denoted:
K : W( A B) (WA WB)
The modal inference rule of necessitation:
Λ A
Λ WA
13
14
Multi-Modal Logics
There exist logic languages with more than
one modal operator
Why do you think?
They may use:
Collection of symbols {[i]}
Each modal [i] has its dual, <i>
<i>A= [i]A.
15
Multi-Modal Logics- Syntax
• Very similar to the syntax of uni-modal
logics, that we already know.
•Every proposition p is a formula.
• If A, B are formulas, then the following are also
formulas:
•
¬A,
A Ù B,
A Ú B,
A B,
AB
• If A is a formula then the following are also
formulas:
•
[i ] A
i A
16
Multi-Modal Logics- Semantics
A frame F for multimodal language is define
as follows –
F=(W,{Ri | i})
W is a non-empty set of worlds
For each i, Ri is a binary relation on W.
A model M is a tupple M=(W,{Ri | i},V)
A valuation V is function
V : P W {T , F }
17
The Semantic Relation
The relation
‘
between a pair (M,w) where
M is a model and w is a world, and a formula
A, is defined recursively as follows:
M , w ‘ p, p P V ( p, w) T
M , w ‘ pA Ù B M , w ‘ A and M , w ‘ B
Similar for the other classical logic connectors.
M , w ‘ [i] A x W if (w, x) Ri then M , x ‘ A
M , w ‘ i A x W s.t. (w, x) Ri Ù M , x ‘ A
18
Multi-Modal Logics
A Logic is defined as same as in uni-modal
logics (includes all tautologies and closed
under MP and substitution).
A logic is said to be normal if it contains the
schemata:
Ki : [i]( A B) ([i] A [i]B)
And satisfies the necessitation
rule for each i.
Λ A
Λ [i ] A
The smallest normal logic is generally denoted
Ki.
19
Multi-Modal Logic - Example
([1]A)
Yesterday, Dan had 2 children.
([2]B)
Tomorrow, Dan will have 3 children.
Let us look on the formula –
[1] A Ù[2]B
Intuitively, It has to be true only in the day in
which his third child was born.
20
Example
Formally, we will define a frame to be- F (W , R1 , R2 )
W – the days during the year.
R1 – all the pairs (dayi, dayi-1).
R2 – all the pairs (dayi, dayi+1).
A world w in model M in which [1]A [2]B will
be true is-
R1
A–T
B-F
A–T
B-F
A–T
B-F
R2
A–T
B-T
A–F
B-T
Dan’s 3rd child
birthday
A–F
B-T
A–F
B-T
21
First Order Modal Logic
Motivation:
Every lecturer strikes.
Yossi is a lecturer.
Thus Yossi strikes.
The formal language –
There are two parts –
A common part for all of the languages.
A signature - unique for every language.
22
First Order Modal Logic
The common part –
{¬, Ù, Ú, , ,W, à }
Operators:
{, }
Quantifies:
Parentheses.
Variables: v1,v2,…
• Syntactic Categories –
• formulas
Will be detailed
• terms
23
First Order Modal Logic
Signature: the unique part of every language -
A non-empty set of function symbols.
A (maybe empty) set of constants.
A (maybe empty) set of predicate symbols.
Terms:
Every variable is a term.
Every constant is a term.
If f is a function symbol and t1,…,tn are terms,
then f(t1,…,tn) is also a term.
24
Definition of a formula
If p is a predicate symbol and t1,…,tn are
terms, the p(t1,…,tn) is an atomic formula.
If A, B are formulas then the following are
also formulas:
A, AB, AB, AB, AB
x.A, x.A
A, A
25
First Order Logic- Semantics
Let L(σ) be a first order language.
When is a formula true?
A Structure M is a pair M=<D,I>, such that –
D – (domain) a non-empty set of objects.
I – an interpretation function of σ:
I [c ] D
I[ f ] Dn D
I [ p] D n
26
FOL – Valuations
A valuation is a function from terms do the
domain
V :xD
However, it is generalized to a function V : o D
from terms to the domain and is defined as:
V[c]= I[c]
V[x] – given by V.
V[f(t1,…,tn)]=I[f](V[t1],…,V[tn])
27
Domains in First Order Modal Logic
This is a problematic issue. Why?
“Tomorrow, everyone will be glad”.
We’ve already asked “When is tomorrow?”
A new question is added- “Who is everyone?”
On Sunday- Everyone includes Yossi,Dan and
Moshe.
On Monday- Everyone includes Yossi,Dan,
Moshe, and Gad.
On Tuesday- Everyone includes Dan, Moshe
and Gad.
28
Domain- 3 natural definitions
1) The set of all individuals existing in the
actual world (D = a).
2) The set of all individuals existing in a given
possible world w (D = w).
3) The set of all the individuals existing in any
world (D = *=UwWw).
29
Domain- 3 natural definitions
The quantifiers have different meanings,
according to the definition of the domain1)
a x means- ‘for all x in the actual world’.
a x means- ‘for an x in the actual world’.
2)
w x means- ‘for all x in the world w’.
w x means- ‘for an x in the world w’.
3)
* x means- ‘for all x’.
* x means- ‘for at least one x’.
30
31
Where is modal logic used?
Modal logic is a widely applicable method of
reasoning for many areas of computer
science.
Artificial Intelligence
Database theory
Distributed systems
Program verification
Cryptography theory
32
AI – Epistemic Logic
Epistemic Logic is the modal logic that
reasons about knowledge and belief.
Philosophy, Artificial Intelligence, Distributed
Systems.
Important: our examples in that part will be
about propositional multi-epistemic logic (no
quantifiers, more than one modal)
33
Epistemic Logic – Syntax
Will be minimally defined, more details – next
lecture of the seminar.
Suppose there are n agents.
Let P { p1 , p2 , p3 ,
}
be a non-empty
set of propositions.
Operators: {¬, Ù, Ú, , ,[i ], i }
[i]φ- agent i knows φ.
<i>φ- agent i knows that φ is true at some
state.
34
Epistemic Logic- Syntax
Formulas are defined as usual.
In addition to reasoning about what each
agent knows, it may be helpful to reason
about:
n
Everyone knows:
Eφ Ù[i]φ
Common knowledge:
Cφ Ù Eφ( k ) ,
k
i 1
Eφ(1) Eφ , Eφ( k 1) E( Eφ( k ) )
35
Applications of Epistemic Logic
(semantics)
In a multi-agent system, there are n agents.
Each agent i has it’s local environment, that
consists of information of what i’s local state is in
the system.
In addition there is a global environment, that
includes information that agents might not
necessarily know but is still important for the
system to run (this information is categorized as
seen from a “bird’s eye” view of the system).
36
Examples (1)
A scrabble game:
Agents i’s local environment:
The letters i contained in its hand.
The letters that have been currently played.
Which words were played by each player.
The current score.
The global environment may contains The letters that haven’t been chosen by any
player.
37
Examples (2)
A distributed system.
Each process is an agent.
The local environment of a process might
contain messages i has sent or received, the
values of local variables, the clock time.
The global environment might include the
number of process, a log file of all the
process’ operations, etc.
38
Applying epistemic logic using
possible worlds semantics
The environments defines a global state.
A global state is a set (se,s1,…,sn) of
environments
Se is the global environment.
Each si is the local environment of agent i.
A run is defined as a function from time to
global states.
A point is a pair (r,m) where r is a run at
some time m (assume time to be the natural
numbers).
39
Applying epistemic logic using
possible worlds semantics
A system is defined as a set of runs. Thus, our
description of a system entails a collection of
interacting agents.
Intuitively, a system is the set of all possible
runs.
At point (r,m), system is in some global state
r(m). Let ri(m) be the local environment for
agent i.
40
Applying epistemic logic using
possible worlds semantics
Note that a system can be viewed in terms of
a frame.
W = a set of points.
Ri = the relation for agent i.
Ri {((r , m),(r ', m ')) | ri (m) r 'i (m ')}
This means that agent i considers (r’,m’)
possible at point (r,m) if I has the same local
environment at both point.
This means, intuitively, that if agent i runs in r
at time m, then he could continue running in r’
at time m’.
41
Applying epistemic logic using
possible worlds semantics
Let be a set of propositions.
These propositions describe facts about the
system as “the system is deadlocked” or “the
value of variable x is 5”.
An interpreted system is a tuple (S,V), where
S is a system and V is a function that maps
propositions in , V(p,s){true, false}, where
p is a proposition and s is a state.
42
Applying epistemic logic using
possible worlds semantics
We associate I=(S,V) with the modal structure
M=(W,R1,…,Rn,V). Thus, agents’ knowledge is
determined by their local environment.
What it means for a formula to be true at
point (r,m) in I?
By applying earlier definitions we get:
(I, r , m) ‘ φ ( M , (r , m)) ‘ φ
43
44
Applying epistemic logic
using axiomatic systems
• Martha puts a spot of mud on the forehead of
each child.
•Each child can see the forehead of the otherA knows that B’s forehead is muddy, and
conversely.
•Neither child knows whether their own
forehead is muddy.
45
Applying epistemic logic
using axiomatic systems
• Martha announces, “At least one of you
has a muddy forehead”.
[Martha said] Ka Kb ( A Ú B)
• Then she asks, “does either of you know
whether your own forehead is muddy?”
[b sees a] Ka ( Kb A Ú Kb ¬A)
• Neither child answers. [b doesn't know] Ka ¬Kb B
• She asks the same question again, and
this time both children answer- “I know
mine is”.
[We want] Ka A
• How did it happen?
46
Definitions
In order to proof the conclusion we have to
take an axiomatic system of classical logic (as
HPC) and add some axioms and rules of
inference:
Distributivity
Ka ( X Y ) ( K a X K aY )
Truth
Ka X X
(Semantically, R is reflexive)
Rule N
X
Ka X
X Y
Rule R
K a X K aY
47
Proof
K a Kb (¬A B)
2. Kb (¬A B) ( Kb ¬A Kb B)
3. Ka Kb (¬A B) Ka ( Kb ¬A Kb B)
4. Ka ( Kb ¬A Kb B)
1.
[Martha said]
Distributivity
Rule R 2
MP 1,3
It means that A knows that if B knows that A’s
forehead is not muddy then B knows his
forehead is muddy!
Dist.: K a ( X Y ) ( K a X K aY )
Truth: Ka X X
X Y
Rule R:
K a X 48K aY
Proof
K a Kb (¬A B)
[Martha said]
2. Kb (¬A B) ( Kb ¬A Kb B)
Distributivity
3. Ka Kb (¬A B) Ka ( Kb ¬A Kb B)
Rule R 1
4. Ka ( Kb ¬A Kb B)
MP 1,3
5. ( Kb ¬A Kb B) (¬Kb B ¬Kb ¬A)
CPL theorem
6. Ka ( Kb ¬A Kb B) Ka (¬Kb B ¬Kb ¬A)
Rule R 5
7. Ka (¬Kb B ¬Kb ¬A)
MP 4,6
8. Ka (¬Kb B ¬Kb ¬A) ( Ka ¬Kb B Ka ¬Kb ¬A) Distributivity
9. K a ¬Kb B K a ¬Kb ¬A
MP 7,8
1.
Dist.: K a ( X Y ) ( K a X K aY )
Truth: Ka X X
X Y
Rule R:
K a X 49K aY
Proof (cont’d)
9. K a ¬Kb B K a ¬Kb ¬A
MP 7,8
It means that A knows that if B doesn’t knows
whether his forehead is muddy then A knows
that it is possible in B’s knowledge that A’s
forehead is muddy!
Remember that: [i]A <i>A
Dist.: K a ( X Y ) ( K a X K aY )
Truth: Ka X X
X Y
Rule R:
K a X 50K aY
Proof (cont’d)
9. K a ¬Kb B K a ¬Kb ¬A
10. K a ¬Kb B
11. K a ¬Kb ¬A
MP 7,8
[b doesn’t know]
MP 9,10
It means that A knows that it is possible in B’s
knowledge that A’s forehead is muddy!
Dist.: K a ( X Y ) ( K a X K aY )
Truth: Ka X X
X Y
Rule R:
K a X 51K aY
Proof (cont’d)
Ka ¬Kb B K a ¬Kb ¬A
K a ¬Kb B
K a ¬Kb ¬A
Ka (¬Kb ¬A Kb A)
13. Ka (¬Kb ¬A Kb A) ( Ka ¬Kb ¬A Ka Kb A)
14. K a ¬Kb ¬A K a Kb A
15. K a Kb A
9.
10.
11.
12.
MP 7,8
[b doesn’t know]
MP 9,10
[b sees a]
Distribution
MP 12,13
MP 11,14
It means that A knows that B knows A’s forehead
is muddy!
Dist.: K a ( X Y ) ( K a X K aY )
Truth: Ka X X
X Y
Rule R:
K a X 52K aY
Proof (cont’d)
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
Ka ¬Kb B K a ¬Kb ¬A
K a ¬Kb B
K a ¬Kb ¬A
Ka (¬Kb ¬A Kb A)
Ka (¬Kb ¬A Kb A) ( Ka ¬Kb ¬A Ka Kb A)
K a ¬Kb ¬A K a Kb A
K a Kb A
Kb A A
K a Kb A K a A
Ka A
Dist.: K a ( X Y ) ( K a X K aY )
Truth: Ka X X
MP 7,8
[b doesn’t know]
MP 9,10
[b sees a]
Distribution
MP 12,13
MP 11,14
Truth
Rule R 16
MP 15,17
X Y
Rule R:
K a X 53K aY
[Vaughan Pratt 1974]
54
Dynamic Logic
We will concentrate on:
Propositional Dynamic Logic
(PDL)
[Fischer & Lander 1977]
55
What is Dynamic Logic?
Program verification ensures that a program is
correct, meaning that any possible input/
output combination is expected based on the
specifications of the program.
A modal logic, called dynamic logic, was
developed to verify programs.
56
PDL Syntax
Let ={p1, p2, p3, … } – a non-empty set of
propositions.
An ‘atomic’ program is a smallest basic
program, meaning it does not consist of other
programs.
Let ={a1, a2, a3, … } – a non-empty set of
atomic programs.
57
PDL Formulas
Formulas:
If p, then p is a formula.
If and are formulas, then , , ,
, are formulas.
If is a formula and is a program, then
[], <> are formulas.
58
PDL Programs
Programs:
If a, then a is a program.
If and are programs, then ;(sequential
composition), (nondeterministic choice),
and *(iteration) are programs.
If
is a formula, then ? (test) is a program.
Operators precedence:
Unary operators.
The operator ‘;’, and the operator .
Classical Logic operators.
59
Program Operators Interpretation
;: means “do and then ”.
: means “do either or (non-
deterministically)”.
*: means “repeat some finite number of
times”.
?: means “test : continue if is true,
otherwise ‘fail’”.
60
Modal Operators Interpretation
[] means that “if terminates, then
holds” or in other terms “after every
terminating execution of , holds”.
<> means that “there is an execution of
that terminates with as true”.
61
Programming Statements
We can write some classical programming
statements, such as loop constructs, using
PDL program operators:
‘if then else ’ =def (?;)(?;)
‘while do ’ =def (?;)*;?
‘repeat until ’ =def ;(?;)*;?
62
PDL Semantics
A modal structure is M=(W,{Ra|a},V).
W is a set of program states.
Ra is one or more binary relation(s) that
determines which states are accessible from
any state in W.
V is a function from {W} to {true, false}.
63
Accessibility Relations
We consider (w,w’)Ra as the case that w is
the initial state of program a and w’ is an
ending state.
Developed accessibility relations:
Rα ; β def {( w, w ') | w '' s.t. wRα w '' w '' Rβ w '}
Rα β def Rα Rβ
Rα* def {(u, v) | u0 ,..., un where n 0, u u0 , v un
s.t. (ui , ui 1 ) Rα for 0 i n 1}
We will give the definition of R? after presenting the
definition of .
64
The Semantic Relation
The relation
‘
between a pair (M,w) where
M is a model and w is a state, and a formula
A, is defined recursively as follows:
M , w ‘ p, p Φ V ( p, w) true
M , w ‘ pA Ù B M , w ‘ A and M , w ‘ B
Similar for the other classical logic connectors.
M , w ‘ [[α] A x W if (w, x) Rα then M , x ‘ A
M,w‘ <
α A x W s.t. (w, x) Rα Ù M , x ‘ A
65
The R? relation
R? =def {(u,u) | M,u }
For example, we can define the accessibility
relation for the while-do program (;)*;?:
Rwhile do def {(u , v) | u0 ,..., un where n 0, u u0 , v un
s.t. M , ui ‘ φ, 0 i n 1 and (ui , ui 1 ) Rα
for 0 i n 1, and M , un ‘ φ}
66
Applications of PDL
A correctness specification is a formal
description of how a program is to behave.
A program is correct if its output meets the
correctness specification.
PDL, and hence dynamic logic, is not well-
suited about program behavior at
intermediary states. Other logics that do so
are process logic and temporal logic.
67
Applications of PDL
PDL is better suited to reasoning about program
behavior with respect to only input and output
states.
For example, the accessibility relation for a
program only contains information about an
input and an output state, i.e., (w,w’)R means
that w’ is an output state when program is run
with initial state w.
Thus, a reasonable restriction for dynamic logic is
to only consider programs that halt (so its
correctness specifications are usually in the form
of input/output).
68
A PDL Example
Let a,b be atomic programs.
Let p be an atomic proposition.
Suppose M=(W,Ra,Rb,V)
W = {s,t,u,v}
Ra = {(u,s),(v,t),(s,u),(t,v)}
Rb = {(u,v),(v,u),(s,t),(t,s)}
s
b
a
p
u
t
a
b
V(p,u) = V(p,v) = true
v
70
s
A PDL Example
Prove:
Mp[(ab*a)*]p
b
a
p
u
t
a
b
v
Proof:
M,wp[(ab*a)*]p
(xW.(w,x)R(ab*a)*M,xp) (M,wp)
What is R(ab*a)*?
71
s
A PDL Example
R(ab*a)*:
b
a
p
u
t
a
b
v
Let’s build it from:
Rb*={(u,u), (u,v), (v,u), (v,v), (s,s), (s,t),
(t,s), (t,t)}
Rab*={(u,s), (u,t), (v,s), (v,t), (s,u), (s,v),
(t,u), (t,v)}
Rab*a={(u,u), (u,v), (v,u), (v,v), (s,s), (s,t),
(t,s), (t,t)}
R(ab*a)*={(u,u), (u,v), (v,u), (v,v), (s,s),
(s,t), (t,s), (t,t)}
72
s
A PDL Example
M,wp[(ab*a)*]p
b
a
p
u
t
a
b
v
(xW.(w,x)R(ab*a)*M,xp) (M,wp)
R(ab*a)*={(u,u), (u,v), (v,u), (v,v), (s,s), (s,t), (t,s),
(t,t)}
If M,wp then w{u,v} and so:
For each accessible state x from w (that are u
and v), M,xp.
If M,wp then w{s,t} and so:
There is an accessible state x from w (for
instance, s itself), such that M,xp.
Thus, Mp[(ab*a)*]p.
73
s
A PDL Example
b
a
p
u
t
a
b
v
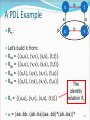
Let: = (aabb(abba)(aabb)*(abba))*
M []
Proof:
M,w []
(xW.(w,x)RM,x) (M,w)
What is R?
74
s
A PDL Example
R:
b
t
a
p
u
a
b
v
Let’s build it from:
Raa = {(u,u), (v,v), (s,s), (t,t)}
Rbb = {(u,u), (v,v), (s,s), (t,t)}
Rab = {(u,t), (v,s), (s,v), (t,u)}
Rba = {(u,t), (v,s), (s,v), (t,u)}
R = {(u,u), (v,v), (s,s), (t,t)}
The
identity
relation RI
= (aabb(abba)(aabb)*(abba))*
75
s
A PDL Example
M,w []
b
a
p
u
t
a
b
v
(xW.(w,x)RM,x) (M,w)
R = {(u,u), (v,v), (s,s), (t,t)}
In conclusion,
The only state accessible from w is w itself.
And so, (xW.(w,x)RM,xp) (M,wp)
Thus, M [].
76
Summary
Modal logic as an extension of classical logic
Possible worlds semantics
Logics and normal logics
Axiomatic systems
Extensions of multi-modal logic.
First order modal logic
Various Applications of modal logic- focus on
artificial intelligence and program verification
77
78