* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Simple Harmonic Motion
Internal energy wikipedia , lookup
Fictitious force wikipedia , lookup
Classical mechanics wikipedia , lookup
Old quantum theory wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Virtual work wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Brownian motion wikipedia , lookup
Heat transfer physics wikipedia , lookup
Jerk (physics) wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Work (thermodynamics) wikipedia , lookup
Thermodynamic system wikipedia , lookup
Equations of motion wikipedia , lookup
Seismometer wikipedia , lookup
Hooke's law wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Centripetal force wikipedia , lookup
Rigid body dynamics wikipedia , lookup
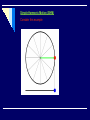
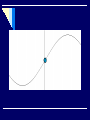
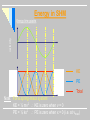
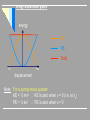
Simple Harmonic Motion Oscillations • Motion is repetitive (Periodic) and the oscillating body moves back and forth around an equilibrium position. • Period: The time required for one full oscillation • • We will focus on constant periods… What are some examples of oscillating bodies/systems? Periodic Motion • Objects that move back and forth periodically are described as oscillating. • These objects move past an equilibrium position, O (where the body would rest if a force were not applied) and their displacement from this position changes with time. • If the time period is independent of the maximum displacement, the motion is isochronous. O E.g. -Oscillating pendulums, watch springs or atoms can all be used to measure time Properties of oscillating bodies A time trace is a graph showing the variation of displacement against time for an oscillating body. Demo: Producing a time-trace of a mass on a spring. Distance sensor connected to computer Amplitude (x0): The maximum displacement (in m) from the equilibrium position (Note that this can reduce over time due to damping). Cycle: One complete oscillation of the body. Period (T): The time (in s) for one complete cycle. Frequency (f): The number of complete cycles made per second (in Hertz or s-1). (Note: f = 1 / T) Angular frequency (ω): Also called angular speed, in circular motion this is a measure of the rate of rotation. In periodic motion it is a constant (with units s-1 or rad s-1) given by the formula… ω = 2π = 2πf T Q. Calculate the angular speed of the hour hand of an analogue watch (in radians per second). Angle in one hour = 2π radians Time for one revolution = 60 x 60 x 12 = 43200s ω = 2π = 1.45 x 10-3 rad s-1 T Simple Harmonic Motion (SHM) Consider this example Hooke’s Law • What is the relationship between the displacement of the spring and the force applied to the spring? • What characteristics of the spring will affect this? • Hooke’s Law: up to its elastic limit, a spring will experience a displacement that is proportional to the force applied to the spring. More on springs… • Restoring Force: • the tension in the spring that works to bring a mass back to its rest position (equilibrium position). • The restoring force is the reaction force to any applied force (i.e. the weight of something hanging from the spring) • This is the force that causes a mass to accelerate around its rest position when it has experienced a displacement away from equilibrium. Simple Harmonic Motion • A special case of periodic oscillations that • • • • can be described by analyzing the forces involved in the motion Hooke’s law can be rewritten as… ma = -k x We are going to define angular frequency as: ω = √ (k / m) Angular frequency has units of Hertz (s-1) Defining relation for SHM: a = -ω2 x • “Simple harmonic motion takes place when a particle that is disturbed away from its fixed equilibrium position experiences an acceleration that is proportional and opposite to its displacement” (from the IB Physics text by Tsokos) Two requirements for SHM: • Must have a fixed equilibrium point • Acceleration, when displaced, must be proportional to the amount of displacement SHM--mathematics • By using calculus, the defining relationship • • • • becomes one that we can put in terms of the angular frequency, the time that has passed, the amplitude of the displacement, and the “phase shift” A = amplitude x = A cos (ωt + Φ) t = time Φ = phase shift ω = angular frequency • Amplitude: the maximum displacement away from the equilibrium (rest) position. • This occurs when the value of the cosine function is equal to 1 • Φ = Phase Shift: recorded in radians; gives an indication of the displacement at t = 0 s. • See diagram on next slide… • Phase difference: ΔΦ = |Φ1 – Φ2| Simple Pendulum… • Is this simple harmonic motion? How do you know? NO! It is not SHM—the acceleration and the displacement are not proportional to each other Period of a pendulum can be found with: T = 2π √(L/g) Q1 Sketch a graph of acceleration against displacement for the oscillating mass shown (take upwards as positive. displacement o a x Q2 Consider this duck, oscillating with SHM… Where is… i. Displacement at a maximum? ii. Displacement zero? C iii. Velocity at a maximum? iv. Velocity zero? v. C A and E Acceleration at a maximum? vi. Acceleration zero? A and E C A and E Damped Oscillations • Any oscillations that are taking place with the presence of one or more resistance forces, such as friction and air resistance. • As a result of resistance forces, oscillations will eventually stop as the energy of its motion is transformed into other forms of energy—primarily thermal energy of both the environment and the system. Types of damping effects: • Under-damping: • Small resistance forces • Oscillations continue, but with a slightly smaller frequency than if force was not there • Amplitude gradually reduces until it approaches 0 and the oscillations stop • The larger the damping force, the longer the period and the faster it will stop oscillating Types of damping effects: • Critical Damping: • The system returns to its equilibrium state as fast as possible without any oscillations • Over-damping: • The system returns to equilibrium without oscillations, but much slower than in critical damping Graphical comparison of damping effects Oscillations and Waves Energy Changes During Simple Harmonic Motion Energy in SHM velocity Energy-time graphs energy KE PE Total Note: For a spring-mass system: KE = ½ mv2 KE is zero when v = 0 PE = ½ kx2 PE is zero when x = 0 (i.e. at vmax) Energy–displacement graphs energy KE PE Total -xo +xo displacement Note: For a spring-mass system: KE = ½ mv2 KE is zero when v = 0 (i.e. at xo) PE = ½ kx2 PE is zero when x = 0 Kinetic energy in SHM We know that the velocity at any time is given by… v = ω √ (xo2 – x2) So if Ek = ½ mv2 then kinetic energy at an instant is given by… Ek = ½ mω2 (xo2 – x2) Potential energy in SHM If a = - ω2 x then the average force applied trying to pull the object back to the equilibrium position as it moves away from the equilibrium position is… F = - ½ mω2x Work done by this force must equal the PE it gains (e.g in the springs being stretched). Thus.. Ep = ½ mω2x2 Total Energy in SHM Clearly if we add the formulae for KE and PE in SHM we arrive at a formula for total energy in SHM: ET = ½ mω2xo2 Summary: Ek = ½ mω2 (xo2 – x2) Ep = ½ mω2x2 ET = ½ mω2xo2 teacherweb.com/CA/.../Berg/SimpleHarmonicMotionweb.ppt sjhs-ibphysics.wikispaces.com/file/view/15+Kinematics+of+SHM.ppt SOURCES