* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Section 1-3: Segments and Their Measures
John Wallis wikipedia , lookup
Functional decomposition wikipedia , lookup
Large numbers wikipedia , lookup
Elementary algebra wikipedia , lookup
Numerical continuation wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Fundamental theorem of algebra wikipedia , lookup
Fundamental theorem of calculus wikipedia , lookup
Cartesian coordinate system wikipedia , lookup
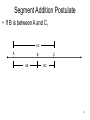
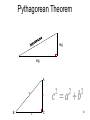
Section 1.3: Segments and Their Measures Goals Use segment postulates Use the Distance Formula to measure distances Anchors •Analyze characteristics and properties of two dimensional geometric shapes and demonstrate understanding of geometric relationship •Find the measure of the side of a right triangle using the Pythagorean Theorem 1 • Postulates Ruler Postulate The points on any line can be matched one to one with the real numbers. The real number that corresponds to a pt is the coordinate of the point. Names of pts A B x1 x2 Coordinates of pts 2 The distance between points A and B on a number line, written as AB, is the absolute value of the difference between the coordinates of A and B. AB is also called the length of AB A B x1 x2 Find the distance between each of the following pairs of points: 12 37 -15 28 3 Segment Addition Postulate • If B is between A and C, AC A B AB C BC 4 Given: R is between A and T. AR = 4x + 2 , RT = 3x , and AT = 8x – 1. Find the length of each segment. A R T •Write a segment addition statement •Substitute algebraic expressions •Solve •Check your answer 5 Given: O is between M and P. MO = x2 - 3 , OP = 4x - 1 , and MP = 8x + 1. Find the length of each segment. M O P •Write a segment addition statement •Substitute algebraic expressions •Solve •Check your answer 6 Using the Distance Formula • Distance Formula • Congruent Segments 7 The Distance Formula • If A(x1, y1) and B(x2, y2) are pts in a coordinate plane, then the distance between A and B is 8 Find the distance between the following pairs of points: 1) A ( 2 , 3 ) B ( 8 , 11 ) 2) C ( 12 , 18 ) D ( 14 , 24 ) No Decimals 9 AB = 10. If A is located at ( 2 ,11) and B is located at ( 8 , y ), what are the possible values of y ? AB ( x2 x1 ) ( y2 y1 ) 2 10 (2 8) 2 (11 y ) 2 10 (6) (11 y ) 2 10 36 (11 y ) 2 100 36 (11 y) 2 2 2 64 (11 y) 2 8 11 y 8 11 y 3 y 8 11 y 19 y 10 CD = 17. If C is located at ( 3 ,1) and D is located at ( x , 16 ), what are the possible values of x ? EF = 15. If E is located at ( -3 ,14) and F is located at ( 6 , y ), which of the following is a possible value of y ? a) -26 b) 14 c) 2 d) -10 11 Pythagorean Theorem leg leg A c B b a C 12