Download Key Stage 2 - WordPress.com

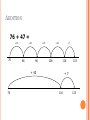
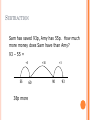
I think of a number and add 6.
My answer is 17, what number did I start with?
11
Well done Chris.
How did you
think that through?
SUMS AND
THINGS FOR
PARENTS!
What can a numerate child do?
By the age of 11 they should :

have a sense of the size of number and
where it fits into the number system

know by heart addition and subtraction
facts to 20, multiplication and division
facts to 10x10, doubles and halves,
complements to 100, multiply and
divide by 10 and 100

use what they know to figure out
answers mentally
What can a numerate child do? (cont.)

calculate accurately and efficiently, both
mentally and on paper, using a range
of strategies

recognise when it is appropriate to use a
calculator- and when it is not- and be
able to use one effectively

explain their methods and reasoning
using correct mathematical terms

judge whether their answers are
reasonable and have strategies for
checking them where necessary
The aim
The aim is for children to do mathematics in
their heads, and if the numbers are too large, to
use pencil and paper to avoid losing track. To do
this children need to learn quick and efficient
methods, including appropriate written
methods.
 All of this relies on knowing number facts to
prevent the need to work out each small stage.
We want children to ask
themselves:
Can I do this in my head?
Can I do this in my head using drawings or
jottings to help?
Do I need to use an expanded/compact
written method?
Do I need a calculator?
ADDITION AND SUBTRACTION
How do you add and subtract?
61 + 45
7800 – 5600
5735 + 3657
5735 + 3990
83 – 68
5002 – 4996
538 - 295
267 + 267
2.5 + 2.7
5.1 - 2.78
ADDITION
2+4=
 My Mum gives me 2
sweets and my Dad
gives me 4 sweets –
how many do I have
altogether?
8+6=
 There are 8 people on
the train then 6 more
get on. How many
people are on the train
now?
||||||||
||||||
ADDITION
76 + 47 =
+10
76
+10
86
+10
96
+10
106
+7
116
+ 40
76
123
+7
116
123
ADDITION
Record steps in addition using partitioning:
14 + 22
14 + 20 = 34
34+ 2 = 36
or
14 + 22
10 + 20 = 30
4+ 2 = 6
80 + 6 = 36
ADDITION
176 + 147 =
100 + 70 + 6
+ 100 + 40 + 7
200 + 110 + 13
= 323
ADDITION

Have a go!

358 + 473 =
SUBTRACTION
Taking away
Finding the difference
8–3=
 Gran baked 8 cakes. I
ate 3 – how many
were left?
2+=5
 I have 2 cats but my
sister has 5. How many
more cats does she
have?
||||||||
||
|||||
SUBTRACTION
We can do subtraction by partitioning:
38 – 14 =
38 – 10 = 28
28 – 4 = 24
SUBTRACTION
Imran has 43 conkers; he gives 24 away to his
friends. How many does he have left?
43 – 24 =
19
23
-4
19 conkers
33
-10
43
-10
SUBTRACTION
Sam has saved 93p, Amy has 55p. How much
more money does Sam have than Amy?
93 – 55 =
+5
55
38p more
+30
60
+3
90
93
SUBTRACTION
8.23 – 4.55 =
+0.45
4.55
3.68
5.00
+3
+0.23
8.00
8.23
SUBTRACTION
A sports stadium holds 9010 spectators. 5643
people attend a football match. How many
empty seats are there?
+ 57
5643
5700
+300
+3010
6000
9010
5643
3367 empty seats
5700
6000
9010
57
+300
+3010
3367
SUBTRACTION

Example: 639 – 424 =
-
600
400
200
+
+
30
20
+
+
9
4
+
10
+
5
=
215
SUBTRACTION

Example: 491 – 155 =
80
-
11
400
+
90
+
1
100
+
50
+
5
300
+
30
+
6
8 11
491
- 155
336
SUBTRACTION

Have a go!

Use a number line:
97 - 68 = 

Use the expanded method:
639 - 291 = 
MULTIPLICATION
MULTIPLICATION

Each child has 2 legs.
How many legs do 4
children have?

There are 6 eggs in a
box. How many in 3
boxes?
|||
|||
|||
|||
|||
|||
2 + 2 + 2 + 2
6
+ 6 + 6
MULTIPLICATION
MULTIPLICATION
MULTIPLICATION


By the end of Key Stage 1, children are expected
to know their x2, x5 and x10 tables.
By the end of Year 4, children should know all
their times tables.
This knowledge is key to them being able to
multiply larger numbers with written methods.
MULTIPLICATION
47 x 8 =
x
8
40
320
7
56 = 376
30
1200
180
7
280
42
37 x 46 =
x
40
6
= 1480
= 222
= 1702
MULTIPLICATION
MULTIPLICATION
MULTIPLICATION

Have a go at using the grid method yourself:
43 x 59 =
x
50
9
40
2000
360
3
150
27
= 2150
= 387
2537
How can you help?
Talk about
how you
do maths
Give praise and
encouragement
Be positive
Ask your
child to
explain
Make sure maths is fun!
FURTHER READING
Recommended reading:
‘Maths for Mums and Dads’
By Rob Eastaway and Mike Askew
ISBN-13: 978-0224086356
.