* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download x - Dalton State
Big O notation wikipedia , lookup
Functional decomposition wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Continuous function wikipedia , lookup
Non-standard calculus wikipedia , lookup
Dirac delta function wikipedia , lookup
History of the function concept wikipedia , lookup
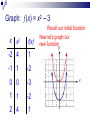
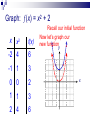
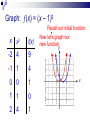
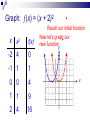
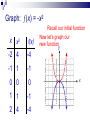
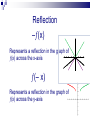
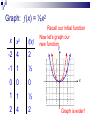
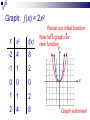
Graphing Transformations It is the supreme art of the teacher to awaken joy in creative expression and knowledge. Albert Einstein Basic Functions Given some fairly simple graphs, we can easily graph more complicated functions by utilizing some specific methods commonly referred to as transformations. Some of the basic functions we will concentrate on are: f(x) = x f(x) = |x| f(x) = x2 f(x) = x3 f(x) =√x IDENTITY FUNCTION (x) = x Domain: (–, ) Range: (–, ) y x f(x) -2 -2 0 0 2 2 x SQUARING FUNCTION (x) = x2 x f(x) Domain: (–, ) Range: [0, ) y -2 4 -1 1 0 0 1 1 2 4 x CUBING FUNCTION (x) = x3 x f(x) Domain: (–, ) Range: (–, ) y -2 -8 -1 -1 0 0 1 1 2 8 x SQUARE ROOT x f(x) (x) = √x Domain: [0, ) Range: [0, ) y 0 0 1 1 4 2 x ABSOLUTE VALUE (x) = |x| x f(x) Domain: (–, ) Range: [0, ) y -2 2 -1 1 0 0 1 1 2 2 x Transformations Let’s investigate what happens when we make slight changes to the basic function. For convenience, we will look at the squaring function (parabola); but the logic will apply to any function. Graph: (x) = x2 – 3 Recall our initial function x x2 f(x) -2 4 1 -1 1 -2 0 0 -3 1 1 -2 2 4 1 Now let’s graph our new functiony x Graph: (x) = x2 – 3 Notice our new function is the same as our initial function, it is just moved down 3 units y Down 3 units x Graph: (x) = x2 + 2 Recall our initial function x x2 f(x) -2 4 6 -1 1 3 0 0 2 1 1 3 2 4 6 Now let’s graph our new functiony x Graph: (x) = x2 + 2 Notice our new function is the same as our initial function, it is just moved up 2 units y x Up 2 units Vertical Shift (x) + c Represents a shift in the graph of (x) up or down c units If c > 0, vertical shift up If c < 0, vertical shift down Graph: (x) = (x – 1)2 Recall our initial function x x2 f(x) -2 4 9 -1 1 4 0 0 1 1 1 0 2 4 1 Now let’s graph our new functiony x Graph: (x) = (x – 1)2 Right 1 unit Notice our new function is the same as our initial function, it is just moved to the right 1 unit y x Notice the 1 to the right is the opposite of -1 applied to the x Graph: (x) = (x + 2)2 Recall our initial function x x2 f(x) -2 4 0 -1 1 1 0 0 4 1 1 9 2 4 16 Now let’s graph our new functiony x Graph: (x) = (x + 2)2 Left 2 units Notice our new function is the same as our initial function, it is just moved to the right 1 unit y x Notice the 2 to the left is the opposite of +2 applied to the x Horizontal Shift (x + c) Represents a shift in the graph of (x) left or right c units If c > 0, shift to the left If c < 0, shift to the right Graph: (x) = -x2 Recall our initial function x x2 f(x) -2 4 -4 -1 1 -1 0 0 0 1 1 -1 2 4 -4 Now let’s graph our new functiony x Graph: (x) = -x2 flipped Notice our new function is the same as our initial function, it is just flipped across the x-axis. y x Reflection –(x) Represents a reflection in the graph of (x) across the x-axis (– x) Represents a reflection in the graph of (x) across the y-axis Graph: (x) = ½x2 Recall our initial function x x2 f(x) -2 4 2 -1 1 ½ 0 0 0 1 1 ½ 2 4 2 Now let’s graph our new functiony x Graph is wider! Graph: (x) = 2x2 Recall our initial function x x2 f(x) -2 4 8 -1 1 2 0 0 0 1 1 2 2 4 8 Now let’s graph our new functiony x Graph is thinner! Vertical Stretching a(x) Represents a stretch in the graph of (x) either toward or away from the y-axis y=4f(x) If |a| < 0 Graph is wider (stretch away form y-axis) If |a| > 0 Graph is thinner (stretch toward form y-axis) y=½f(x) Operations of Functions Given two functions and g, then for all values of x for which both (x) and g(x) are defined, the functions + g, – g, g, and /g are defined as follows. f g x f ( x ) g( x ) Sum f g x f ( x ) g( x ) Difference fg x f ( x ) g( x ) Product f f (x) g x g( x ) , g( x ) 0 Quotient f g x f x g x This just says that to find the sum of two functions, add them together. You should simplify by finding like terms. f x 2 x 3 g x 4 x 1 2 3 f g 2x 3 4x 1 2 3 4x 2x 4 3 2 Combine like terms & put in descending order f g x f x g x To find the difference between two functions, subtract the first from the second. CAUTION: Make sure you distribute the – to each term of the second function. You should simplify by combining like terms. f x 2 x 3 2 g x 4 x 1 3 f g 2x 3 4x 1 2 3 Distribute negative 2 x 3 4 x 1 4 x 2 x 2 2 3 3 2 f g x f x gx To find the product of two functions, put parenthesis around them and multiply each term from the first function to each term of the second function. f x 2 x 3 g x 4 x 1 2 3 f g 2x 3 4x 1 2 3 8 x 2 x 12 x 3 5 2 3 FOIL Good idea to put in descending order but not required. f f x x g x g To find the quotient of two functions, put the first one over the second. f x 2 x 3 2 f 2x 3 3 g 4x 1 2 g x 4 x 1 3 Nothing more you could do here. (If you can reduce these you should). So the first 4 operations on functions are pretty straight forward. The rules for the domain of functions would apply to these combinations of functions as well. The domain of the sum, difference or product would be the numbers x in the domains of both f and g. For the quotient, you would also need to exclude any numbers x that would make the resulting denominator 0. Composition of Functions If and g are functions, then the composite function, or composition, of g and is defined by g f x g f ( x ) . The domain of g f is the set of all numbers x in the domain of such that (x) is in the domain of g. Composition of Functions Composition is simply taking the result of one function and sticking it into the other function x g x g Function Machine f Function Machine f g x f g x f gx This is read “f composition g” and means to copy the f function down but where ever you see an x, substitute in the g function. f x 2 x 3 2 g x 4 x 1 3 2 f g 2 4x 1 3 3 FOIL first and then distribute the 2 32 x 16 x 2 3 32 x 16 x 5 6 3 6 3 g f x g f x This is read “g composition f” and means to copy the g function down but where ever you see an x, substitute in the f function. f x 2 x 3 g x 4 x 1 2 3 3 g f 4 2x 3 1 2 You could multiply this out but since it’s to the 3rd power we won’t