* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Phase Transformations
Viscoelasticity wikipedia , lookup
Bose–Einstein condensate wikipedia , lookup
Superconductivity wikipedia , lookup
Ferromagnetism wikipedia , lookup
Temperature wikipedia , lookup
Heat transfer physics wikipedia , lookup
Crystal structure wikipedia , lookup
Spinodal decomposition wikipedia , lookup
Energy applications of nanotechnology wikipedia , lookup
State of matter wikipedia , lookup
Sol–gel process wikipedia , lookup
Thermodynamic temperature wikipedia , lookup
Dislocation wikipedia , lookup
Colloidal crystal wikipedia , lookup
Paleostress inversion wikipedia , lookup
Freeze-casting wikipedia , lookup
Work hardening wikipedia , lookup
Shape-memory alloy wikipedia , lookup
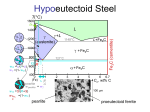
PHASE TRANSFORMATIONS Nucleation Growth APPLICATIONS Transformations in Steel Precipitation Solidification & crystallization Glass transition Recovery, Recrystallization & Grain growth Phase Transformations in Metals and Alloys David Porter & Kenneth Esterling Van Nostrand Reinhold Co. Ltd., New York (1981) PHASE TRANSFORMATIONS Based on Mass transport Diffusional Martensitic PHASE TRANSFORMATIONS Based on order 1nd order nucleation & growth 2nd order Entire volume transforms Bulk Gibbs free energy ↓ Energies involved Interfacial energy ↑ Strain energy ↑ Solid-solid transformation New interface created Volume of transforming material The concepts are illustrated using solidification of a metal 1nd order nucleation & growth Trasformation → = Nucleation of phase + Growth till is exhausted Liquid → Solid phase transformation On cooling just below Tm solid becomes stable But solidification does not start E.g. liquid Ni can be undercooled 250 K below Tm ↑t Solid stable Liquid stable G G → Solid (GS) G → ve T G → +ve Tm T - Undercooling T → Liquid (GL) “For sufficient Undercooling” Solidification Nucleation = Nucleation + Growth Homogenous Nucleation Heterogenous Liquid → solid walls of container, inclusions Solid → solid inclusions, grain boundaries, dislocations, stacking faults The probability of nucleation occurring at point in the parent phase is same throughout the parent phase In heterogeneous nucleation there are some preferred sites in the parent phase where nucleation can occur Neglected in L → S transformations Homogenous nucleation Free energy change on nucleation Reduction in bulk free energy increase in surface energy increase in strain energy ΔG (Volume).( G ) (Surface). ( ) 4 3 ΔG r .(Gv ) 4r 2 .( ) 3 Gv f (T ) r3 r2 1 4 ΔG r 3 .(Gv ) 4r 2 .( ) 3 By setting dG/dr = 0 the critical values (corresponding to the maximum) are obtained (denoted by superscript *) Reduction in free energy is obtained only after r0 is obtained dG 0 dr 2 r Gv As Gv is ve, r*is +ve 2 * * r1 0 r2 Gv Trivial dG 0 dr * G 0 3 r0 Gv G → G 0 3 16 G * 3 Gv2 r* Embryos r0 Supercritical nuclei r → Gv f (T ) The bulk free energy reduction is a function of undercooling Turnbull approximation Tm Tm2 16 3 G 3 T 2 H 2 Decreasing G* G → Decreasing r* r → Rate of nucleation = dN I dt No. of critical sized particles N Nt e * G * kT No. of particles/volume in L x Frequency with which they become supercritical ' s e * H d kT → lattice vibration frequency (~1013 /s) s* atoms of the liquid facing the nucleus Critical sized nucleus Jump taking particle to supercriticality → nucleated (enthalpy of activation = Hd) Critical sized nucleus I Nt s e * G * H d kT G* ↑ I ↓ T↑ I ↑ T = Tm → G* = → I = 0 T (K) → Increasing T Tm 0 I → T=0→I=0 Heterogeneous nucleation Consider the nucleation of from on a planar surface of inclusion Interfacial Energies Created Alens Created Acircle Lost Acircle Cos Surface tension force balance Cos ΔG (Vlens )Gv (A lens ) ( Acircle ) ( Acircle ) Vlens = h2(3r-h)/3 Alens = 2rh h = (1-Cos)r rcircle = r Sin dG 0 dr * hetero r 2 G * hetero Gv G G*hetero / G*homo → * hetero 1 3 4 3 2 3 Cos Cos 2 3 Gv 1 * Ghomo 2 3Cos Cos 3 4 G*hetero (0o) = 0 no barrier to nucleation G*hetero (180o) = G*homo no benefit 0.75 G*hetero (90o) = G*homo/2 0.5 Cos 0.25 Complete wetting No wetting Partial wetting 0 0 30 60 90 120 (degrees) → 150 180 0 I homo I homo e * Ghomo kT = f(number of nucleation sites) I hetero I 0 hetero e * Ghetero kT = f(number of nucleation sites) ~ 1026 ~ 1042 BUT the exponential term dominates Ihetero > Ihomo Choice of heterogeneous nucleating agent Small value of Cos Choosing a nucleating agent with a low value of (low energy interface) (Actually the value of ( ) will determine the effectiveness of the heterogeneous nucleating agent → high or low ) low value of → Crystal structure of and are similar and lattice parameters are as close as possible Seeding rain-bearing clouds → AgI or NaCl → nucleation of ice crystals Ni (FCC, a = 3.52 Å) is used a heterogeneous nucleating agent in the production of artificial diamonds (FCC, a = 3.57 Å) from graphite Trasformation → = Nucleation of phase + Growth till is exhausted Growth At transformation temperature the probability of jump of atom from → (across the interface) is same as the reverse jump Growth proceeds below the transformation temperature, wherein the activation barrier for the reverse jump is higher Hd Hd – vatom Gv phase phase Transforma tion rate f(Nucleati on rate, Growth rate) T dX dt f (I , U ) Tm Increasing T U Xβ 1 e π I U3 t 4 3 Maximum of growth rate usually at higher temperature than maximum of nucleation rate T T (K) → I 0 I, U, T → Xβ 1 e π I U3 t 4 3 1.0 X → 0.5 0 t → Time – Temperature – Transformation (TTT) diagrams A type of phase diagram Small driving force for nucleation 0 Tm T Replot T (rate sec1) → T (K) → T (K) → Tm 0 Time for transformation t (sec) → Growth sluggish TTT diagram → phase transformation T (K) → Increasing % transformation 99% = finish 1% = start t (sec) → Turnbull’s approximation Δh heat of fusion Tm T T G h h Tm Tm Solid (GS) G → G T Liquid (GL) Tm T → 16 3 Tm G 3 hT * 2 APPLICATIONS Phase Transformations in Steel Precipitation Solidification and crystallization Glass transition Recovery recrystallization & grain growth Phase Transformations in Steel Fe-Cementite diagram Peritectic L+→ Eutectic L → + Fe3C L 1493ºC L+ 0.1 %C 1147ºC 2.06 + Fe3C Eutectoid → + Fe3C 723ºC + Fe3C T → 0.025 %C Fe 0.16 0.8 4.3 %C → Fe3C 6.7 Time- Temperature-Transformation (TTT) Curves – Isothermal Transformation Eutectoid steel (0.8%C) 800 723 Eutectoid temperature Austenite Coarse Pearlite 600 Fine Pearlite + Bainite T → 500 400 300 Not an isothermal transformation 200 100 Bainite Ms Austenite Mf Martensite 0.1 1 102 10 t (s) → 103 104 105 Time- Temperature-Transformation (TTT) Curves – Isothermal Transformation Eutectoid steel (0.8%C) 800 723 Eutectoid temperature Austenite Pearlite 600 + Fe3C T → 500 Pearlite + Bainite 400 Bainite 300 200 100 Ms Mf Martensite 0.1 1 102 10 t (s) → 103 104 105 Continuous Cooling Transformation (CCT) Curves Eutectoid steel (0.8%C) 800 723 Austenite Eutectoid temperature 600 Pearlite T → 500 Original TTT lines 400 300 Cooling curves Constant rate 200 100 Ms Mf Martensite 0.1 1 T2 T1 102 10 t (s) → 103 104 105 Different cooling treatments Eutectoid steel (0.8%C) 800 723 M = Martensite 600 P = Pearlite T → 500 400 300 200 Coarse P 100 M 0.1 1 Fine P M +P 102 10 t (s) → 103 104 105 Pearlite [1] [1] → + Fe3C Nucleation and growth Heterogeneous nucleation at grain boundaries Interlamellar spacing is a function of the temperature of transformation Lower temperature → finer spacing → higher hardness [1] Physical Metallurgy for Engineers by Donald S Clark and Wilbur R Varney (Second Edition) Affiliated EastWest Press Pvt. Ltd., New Delhi, 1962 Bainite [1] [1] Bainite formed at 348oC Bainite formed at 278oC → + Fe3C** Nucleation and growth Acicular, accompanied by surface distortions ** Lower temperature → carbide could be ε carbide (hexagonal structure, 8.4% C) Bainite plates have irrational habit planes Ferrite in Bainite plates possess different orientation relationship relative to the parent Austenite than does the Ferrite in Pearlite [1] Physical Metallurgy for Engineers by Donald S Clark and Wilbur R Varney (Second Edition) Affiliated EastWest Press Pvt. Ltd., New Delhi, 1962 Martensite ( FCC ) 0.8 %C Quench ' ( BCT ) 0.8 %C Possible positions of Carbon atoms Only a fraction of the sites occupied FCC Austenite C along the c-axis obstructs the contraction FCC Austenite Alternate choice of Cell 20% contraction of c-axis 12% expansion of a-axis Tetragonal Martensite Austenite to Martensite → 4.3 % volume increase In Pure Fe after the Matensitic transformation c=a Refer Fig.9.11 in textbook Martensite The martensitic transformation occurs without composition change The transformation occurs by shear without need for diffusion The atomic movements required are only a fraction of the interatomic spacing The shear changes the shape of the transforming region → results in considerable amount of shear energy → plate-like shape of Martensite The amount of martensite formed is a function of the temperature to which the sample is quenched and not of time Hardness of martensite is a function of the carbon content → but high hardness steel is very brittle as martensite is brittle Steel is reheated to increase its ductility → this process is called TEMPERING Hardness (Rc) → 60 Harness of Martensite as a function of Carbon content 40 20 % Carbon → 0.2 0.4 0.6 Properties of 0.8% C steel Hardness (Rc) Tensile strength (MN / m2) Coarse pearlite 16 710 Fine pearlite 30 990 Bainite 45 1470 Martensite 65 - Martensite tempered at 250 oC 55 1990 Constituent Tempering ' ( BCT ) Martensite Temper ( BCC ) Fe3C (OR ) Ferrite Cementite Heat below Eutectoid temperature → wait→ slow cooling The microstructural changes which take place during tempering are very complex Time temperature cycle chosen to optimize strength and toughness Tool steel: As quenched (Rc 65) → Tempered (Rc 45-55) MARTEMPERING To avoid residual stresses generated during quenching Austenized steel is quenched above Ms for homogenization of temperature across the sample The steel is then quenched and the entire sample transforms simultaneously 800 Tempering follows Eutectoid temperature 723 Austenite Pearlite 600 + Fe3C 500 Pearlite + Bainite 400 Bainite T → Martempering 300 Austempering AUSTEMPERING Ms 200 Mf 100 Martensite 0.1 1 10 To avoid residual stresses generated during quenching Austenized steel is quenched above Ms Held long enough for transformation to Bainite 102 t (s) → 103 104 105 ALLOY STEELS Various elements like Cr, Mn, Ni, W, Mo etc are added to plain carbon steels to create alloy steels The alloys elements move the nose of the TTT diagram to the right → this implies that a slower cooling rate can be employed to obtain martensite → increased HARDENABILITY The ‘C’ curves for pearlite and bainite transformations overlap in the case of plain carbon steels → in alloy steels pearlite and bainite transformations can be represented by separate ‘C’ curves ROLE OF ALLOYING ELEMENTS Interstitial Segregation / phase separation Solid solution Substitutional Element Added Compound (new crystal structure) Plain Carbon Steel Alloying elements • + Simplicity of heat treatment and lower cost • Low hardenability • Loss of hardness on tempering • Low corrosion and oxidation resistance • Low strength at high temperatures • ↑ hardenability • Provide a fine distribution of alloy carbides during tempering • ↑ resistance to softening on tempering • ↑ corrosion and oxidation resistance • ↑ strength at high temperatures • Strengthen steels that cannot be quenched • Make easier to obtain the properties throughout a larger section • ↑ Elastic limit (no increase in toughness) • Alter temperature at which the transformation occurs • Alter solubility of C in or Iron • Alter the rate of various reactions TTT diagram for Ni-Cr-Mo low alloy steel 800 Pearlite Austenite 600 T → 500 400 300 200 100 Bainite Ms Mf Martensite ~1 min t → Precipitation The presence of dislocation weakens the crystal → easy plastic deformation Putting hindrance to dislocation motion increases the strength of the crystal Fine precipitates dispersed in the matrix provide such an impediment Strength of Al → 100 MPa Strength of Duralumin (Al + 4% Cu + other alloying elements) → 500 MPa Al rich end of the Al-Cu phase diagram L T (ºC) → 600 400 200 Al Sloping Solvus line high T → high solubility low T → low solubility of Cu in Al 15 30 % Cu → 45 60 + →+ Slow equilibrium cooling gives rise to coarse precipitates which is not good in impeding dislocation motion.* 4 % Cu ( FCC) ( FCC) CuAl2 (Tetragonal ) slowcool 0.5 % Cu 52 % Cu 4 % Cu 550o C RT RT *Also refer section on Double Ended Frank-Read Source in the chapter on plasticity: max = Gb/L To obtain a fine distribution of precipitates the cycle A → B → C is used Note: Treatments A, B, C are for the same composition B A C + 4 % Cu A Heat (to 550oC) → solid solution supersaturated solution B C Quench (to RT) → Increased vacancy concentration Age (reheat to 200oC) → fine precipitates Hardness → 100oC 180oC 20oC Log(t) → Higher temperature less time of aging to obtain peak hardness Lower temperature increased peak hardness optimization between time and hardness required Hardness → 180oC Peak-aged Dispersion of fine precipitates (closely spaced) Coarsening of precipitates with increased interparticle spacing Overaged Underaged Log(t) → Region of solid solution strengthening (no precipitation hardening) Region of precipitation hardening (but little solid solution strengthening) Peak-aged CRSS Increase → Hardness → 180oC Log(t) → Particle shearing Particle By-pass 1 r r Particle radius (r) → 1 2 r f (t ) Due to large surface to volume ratio the fine precipitates have a tendency to coarsen → small particles dissolve and large particles grow Coarsening ↓ in number of particles ↑ in interparticle spacing reduced hindrance to dislocation motion (max = Gb/L) Solidification and Crystallization Metals G* Thermodynamic ↑ Hfusion 1 H 2fusion High → (10-15) kJ / mole Crystallization favoured by Kinetic ↓ Hd Log [Viscosity ()] Low → (1-10) Poise Enthalpy of activation for diffusion across the interface Difficult to amorphize metals Very fast cooling rates ~106 K/s are used for the amorphization of alloys → splat cooling, melt-spinning. Fine grain size bestows superior mechanical properties on the material High nucleation rate and slow growth rate fine grain size ↑ Cooling rate lesser time at temperatures near Tm , where the peak of growth rate (U) lies ↑ nucleation rate Cooling rates ~ (105 – 106) K/s are usually employed Grain refinement can also be achieved by using external nucleating agents Single crystals can be grown by pulling a seed crystal out of the melt T (K) → Tm 0 U I I, U → Silicates Thermodynamic ↑ Hfusion low Crystallization favoured by Kinetic ↓ Hd Log [Viscosity ()] High → (1000) Poise Enthalpy of activation for diffusion across the interface Easily amorphized Certain oxides can be added to silica to promote crystallization In contrast to metals silicates, borates and phosphates tend to form glasses Due to high cation-cation repulsion these materials have open structures In silicates the difference in total bond energy between periodic and aperiodic array is small (bond energy is primarily determined by the first neighbours of the central cation within the unit Glass-ceramic (pyroceram) A composite material of glass and ceramic (crystals) can have better thermal and mechanical properties But glass itself is easier to form (shape into desired geometry) Heterogenous nucleating agents (e.g. TiO2) added (dissolved) to molten glass Shaping of material in glassy state TiO2 is precipitated as fine particles Held at temperature of maximum nucleation rate (I) Heated to temperature of maximum growth rate Growth Tmaximum U Nucleation T → Tmaximum I Glass t → Partially crystallized Glass Even at the end of the heat treatment the material is not fully crystalline Fine crystals are embedded in a glassy matrix Crystal size ~ 0.1 m (typical grain size in a metal ~ 10 m) Ultrafine grain size good mechanical properties and thermal shock resistance Cookware made of pyroceram can be heated directly on flame Glass Transition Volume → “All materials would amorphize on cooling unless crystallization intervenes” Or other extensive thermodynamic property → S, H, E Glass Crystal T → Tg Tm Glass transition temperature Volume → Change in slope T → Tf Fictive temperature (temperature at which glass is metastable if quenched instantaneously to this temperature) → can be taken as Tg Effect of rate of cooling Volume → T1 T2 As more time for atoms to arrange in closer packed configuration T1 T2 Slower cooling T → Lower volume Slower cooling Higher density Lower Tg On crystallization the viscosity abruptly changes from ~100 → ~1020 Pa s A solid can be defined a material with a viscosity > 1012 Poise Log (viscosity) → Crystal Glass Supercooled liquid T → Tg Tm Cool liquid Heat glass Tg Tx Often metallic glasses crystallize before Tg Please read up paragraph on glassy polymers → p228 in text book Recovery, Recrystallization & Grain Growth Plastic deformation in the temperature range (0.3 – 0.5) Tm → COLD WORK ↑ point defect density Cold work ↑ dislocation density Point defects and dislocations have strain energy associated with them (1 -10) % of the energy expended in plastic deformation is stored in the form of strain energy Annealed material dislocation ~ (10 10 ) 6 9 Cold work Stronger material dislocation ~ (1012 1014 ) ↑ point defect density Anneal Cold work Material tends to lose the stored strain energy ↑ dislocation density Increase in strength of the material Low temperature Cold work Softening of the material Recovery Anneal High temperature Recrystallization Cold work Anneal Recovery Recrystallization Grain growth ↑ Strength ↑ Hardness Cold work ↑ Electrical resistance ↓ Ductility Changes occur to almost all physical and mechanical properties X-Ray diffration ► Laue patterns of single crystals show pronounced asterism → due to lattice curvatures ► Debye-Scherrer photographs show line broadning → Residual stresses + deformations Recovery Recovery takes place at low temperatures of annealing “Apparently no change in microstructure” Excess point defects created during Cold work are absorbed: ► at surface or grain boundaries ► by dislocation climb Random dislocations of opposite sign come together and annihilate each other Dislocations of same sign arrange into low energy configurations: ► Edge → Tilt boundaries ► Screw → Twist boundaries POLYGONIZATION Overall reduction in dislocation density is small POLYGONIZATION Bent crystal Low angle grain boundaries Recrystallization Trecrystallization (0.3 – 0.5) Tm “Nucleation” and growth of new, strain free crystals Nucleation of new grains in the usual sense may not be present and grain boundary migrates into a region of higher dislocation density G (recrystallization) = G (deformed material) – G (undeformed material) TRecrystallization is the temperature at which 50 % of the material recrystallizes in 1 hour Region of higher dislocation density Direction of grain boundary migration Region of lower dislocation density Further points about recrystallization Deformation ↑ recrystallization temperature (Trecrystallization) ↓ Initial grain size ↓ recrystallization temperature ↓ High cold work + low initial grain size finer recrystallized grains ↑ cold work temperature lower strain energy stored ↑ recrystallization temperature Rate of recrystallization = exponential function of temperature Trecrystallization = strong function of the purity of the material Trecrystallization (very pure materials) ~ 0.3 Tm Trecrystallization (impure) ~ (0.5 – 0.6) Tm ► Trecrystallization (99.999% pure Al) ~ 75oC Trecrystallization (commercial purity) ~ 275oC The impurity atoms segregate to the grain boundary and retard their motion → Solute drag (can be used to retain strength of materials at high temperatures) The impurity atoms seggregate to the grain boundary and retard their motion → Solute drag (can be used to retain strength of materials at high temperatures) Second phase particles also pin down the grain boundary during its migration Hot Work and Cold Work Hot Work Plastic deformation above TRecrystallization Hot Work Cold Work Plastic deformation below TRecrystallization Cold Work Recrystallization temperature (~ 0.4 Tm) Grain growth Globally ► Driven by reduction in grain boundary energy Locally ► Driven by bond maximization (coordination number maximization) Bonded to 4 atoms Bonded to 3 atoms Direction of grain boundary migration Boundary moves towards its centre of curvature JUMP Electical conductivity Internal stress Ductility Tensile strength Cold work Recovery Recrystallization Grain growth