* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download AÙp löïc chuû ñoäng vaø bò ñoäng cuûa ñaát rôøi Thay ñoåi tyû
Survey
Document related concepts
Transcript
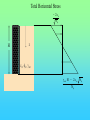
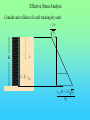
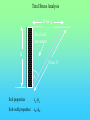
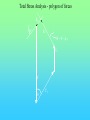
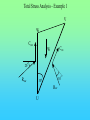
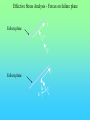
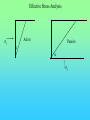
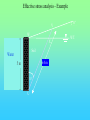
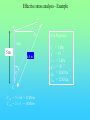
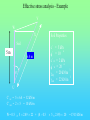
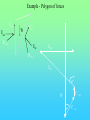
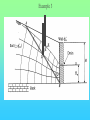
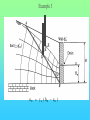
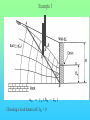
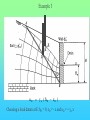
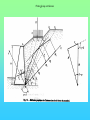
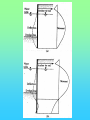
Chöông 5 AÙp löïc ñaát – TÖÔØNG CHAÉN Earth Pressures on Retaining walls Rankine’s Method Modes of failure F Modes of failure F The force F may be provided by • friction at the base (gravity retaining walls) Modes of failure F The force F may be provided by • friction at the base (gravity retaining walls) • founding the wall into the ground (sheet retaining walls) Modes of failure F The force F may be provided by • friction at the base (gravity retaining walls) • founding the wall into the ground (sheet retaining walls) • anchors and struts Modes of failure F The force F may be provided by • friction at the base (gravity retaining walls) • founding the wall into the ground (sheet retaining walls) • anchors and struts • external loads Modes of failure 1. ACTIVE Failure If the force F is too small failure of the wall will occur with soil pushing the wall out. F direction of soil movement Modes of failure 1. ACTIVE Failure If the force F is too small failure of the wall will occur with soil pushing the wall out. F direction of soil movement For most retaining walls active failure is the primary concern. Modes of failure 1. PASSIVE Failure If the force F is too large failure of the wall will occur with the wall pushing into the soil. F direction of soil movement Modes of failure 1. PASSIVE Failure If the force F is too large failure of the wall will occur with the wall pushing into the soil. F direction of soil movement This mode of failure is usually only relevant when large external forces are being applied. Modes of failure 1. PASSIVE Failure If the force F is too large failure of the wall will occur with the wall pushing into the soil. F direction of soil movement This mode of failure is usually only relevant when large external forces are being applied. However, local passive conditions may occur if any part of the wall moves towards the soil. Rankine’s theory • Assume that the wall is frictionless • The normal stress acting on the wall will thus be a principal stress • If the wall is vertical and the soil surface horizontal the vertical and horizontal stresses throughout the retained soil mass will be the principal stresses • The vertical stress may then be calculated in the usual way Rankine’s theory • Assume that the wall is frictionless • The normal stress acting on the wall will thus be a principal stress • If the wall is vertical and the soil surface horizontal the vertical and horizontal stresses throughout the retained soil mass will be the principal stresses • The vertical stress may then be calculated in the usual way d1 d2 g1 g2 z The vertical total stress at depth z is given by v g 1 d1 g 2 ( z d1 ) Rankine’s theory • Assume that the horizontal stress can be calculated from the failure criterion. That is the retained soil is assumed to be everywhere at failure. Rankine’s theory • Assume that the horizontal stress can be calculated from the failure criterion. That is the retained soil is assumed to be everywhere at failure. • From the Mohr-Coulomb failure criterion we have 1 N 3 2 c N Rankine’s theory • Assume that the horizontal stress can be calculated from the failure criterion. That is the retained soil is assumed to be everywhere at failure. • From the Mohr-Coulomb failure criterion we have 1 N 3 2 c N • For active failure the horizontal stress will reduce to its minimum value. That is h = 3 the minimum principal stress, and v = 1 . Rankine’s theory • Assume that the horizontal stress can be calculated from the failure criterion. That is the retained soil is assumed to be everywhere at failure. • From the Mohr-Coulomb failure criterion we have 1 N 3 2 c N • For active failure the horizontal stress will reduce to its minimum value. That is h = 3 the minimum principal stress, and v = 1 . • The minimum (Active) horizontal stress is then h min v 2 c N N Rankine’s theory • For passive failure the horizontal stress will increase to its maximum value. That is h = 1 the maximum principal stress, and v = 3. Rankine’s theory • For passive failure the horizontal stress will increase to its maximum value. That is h = 1 the maximum principal stress, and v = 3. • The maximum (Passive) horizontal stress is then h max N v 2 c N Rankine’s theory • For passive failure the horizontal stress will increase to its maximum value. That is h = 1 the maximum principal stress, and v = 3. • The maximum (Passive) horizontal stress is then h max N v 2 c N • If the vertical stress stays constant the horizontal stress is bounded by the active and passive values. Rankine’s theory • For passive failure the horizontal stress will increase to its maximum value. That is h = 1 the maximum principal stress, and v = 3. • The maximum (Passive) horizontal stress is then h max N v 2 c N • If the vertical stress stays constant the horizontal stress is bounded by the active and passive values. • In the Rankine method a stress state is found that is in equilibrium with the applied loads and has the soil at failure. In plasticity theory this approach is referred to as a lower bound method, a method which can be shown to produce safe, conservative solutions. Rankine’s theory The relation between the active and passive pressures may be shown graphically by considering Mohr circles. t t c tan h v Rankine’s theory The relation between the active and passive pressures may be shown graphically by considering Mohr circles. t t c tan hmin v Rankine’s theory The relation between the active and passive pressures may be shown graphically by considering Mohr circles. t t c tan hmin v hmax Total Stress Analysis The Mohr-Coulomb failure criterion must be expressed in terms of total stress, using undrained parameters cu, u. Total Stress Analysis The Mohr-Coulomb failure criterion must be expressed in terms of total stress, using undrained parameters cu, u. A total stress analysis is only appropriate if soil remains undrained. It can only be used in the short term for soils with low permeabilities. Total Stress Analysis The Mohr-Coulomb failure criterion must be expressed in terms of total stress, using undrained parameters cu, u. A total stress analysis is only appropriate if soil remains undrained. It can only be used in the short term for soils with low permeabilities. For the undrained active failure of a wall we have h v 2 cu N N Total Stress Analysis The Mohr-Coulomb failure criterion must be expressed in terms of total stress, using undrained parameters cu, u. A total stress analysis is only appropriate if soil remains undrained. It can only be used in the short term for soils with low permeabilities. For the undrained active failure of a wall we have h where N = v 2 cu N N 1 + sin u 1 - sin u and for a homogeneous soil layer v = gsat z Total Horizontal Stress 2 cu N H z cu, u, gsat g sat H 2 c u N N Total Horizontal Stress 2 cu N H z cu, u, gsat g sat H 2 c u N N If u is non-zero this implies that the undrained strength varies with depth. The soil must be saturated to use a total stress (undrained) analysis. Tension cracks • The analysis indicates negative, tensile, stresses at the surface. • Soil particles cannot provide tension • The negative stresses have to come from suctions in the pore water • It is difficult to rely on the tensile forces and they are usually ignored • The tensile stresses reduce the force required for stability of the wall. Ignoring the tensile stresses therefore gives a more conservative solution. Tension cracks The horizontal stress distribution becomes z0 z H cu, u gsat g sat H 2 c u N N Tension cracks The horizontal stress distribution becomes z0 z H cu, u gsat g sat H 2 c u N The depth of the tensile region z0 may be determined from h = 0 v 2 cu N 2 cu N z0 g sat g sat z 0 N Tension cracks In the tensile region a crack can develop. Tension cracks In the tensile region a crack can develop. If water is available it can fill the crack, and reduce the stability of the wall. The horizontal stresses on the wall become. Tension cracks In the tensile region a crack can develop. If water is available it can fill the crack, and reduce the stability of the wall. The horizontal stresses on the wall become. Water z0 gw z0 Soil g sat H 2 c u N N Effective Stress Analysis The Mohr-Coulomb failure criterion must be expressed in terms of effective stress, using effective parameters c’, ’. Effective Stress Analysis The Mohr-Coulomb failure criterion must be expressed in terms of effective stress, using effective parameters c’, ’. An effective stress analysis is always appropriate, irrespective of the drainage conditions. To perform an effective stress analysis the pore water pressures must be known. This usually limits effective stress analysis to investigation of long term stability. Effective Stress Analysis The Mohr-Coulomb failure criterion must be expressed in terms of effective stress, using effective parameters c’, ’. An effective stress analysis is always appropriate, irrespective of the drainage conditions. To perform an effective stress analysis the pore water pressures must be known. This usually limits effective stress analysis to investigation of long term stability. For active failure of a wall we have h v 2 c N N Effective Stress Analysis The Mohr-Coulomb failure criterion must be expressed in terms of effective stress, using effective parameters c’, ’. An effective stress analysis is always appropriate, irrespective of the drainage conditions. To perform an effective stress analysis the pore water pressures must be known. This usually limits effective stress analysis to investigation of long term stability. For active failure of a wall we have h where and N = v 2 c N N 1 + sin 1 - sin ’v = v - u Effective Stress Analysis Consider active failure of a wall retaining dry sand 2 c N H z c’, ’, gdry g dry H 2 c N N Effective Stress Analysis • The use of values of c’, ’ associated with peak failure leads to the prediction of impossible tensile stresses. • It is generally more appropriate and safer to use ultimate or critical state parameters, c’ = 0, ’ = ’ult • Using the critical state parameters a larger active force is required for wall stability, and hence a safer estimate is obtained Effective Stress Analysis • The use of values of c’, ’ associated with peak failure leads to the prediction of impossible tensile stresses. • It is generally more appropriate and safer to use ultimate or critical state parameters, c’ = 0, ’ = ’ult • Using the critical state parameters a larger active force is required for wall stability, and hence a safer estimate is obtained c’ , ’ c’ = 0, ’ = ’ult Effective Stress Analysis • For passive failure the horizontal stresses on a wall retaining dry sand are given by h g dry z N 2 c N Effective Stress Analysis • For passive failure the horizontal stresses on a wall retaining dry sand are given by h g dry z N 2 c N • In this case the critical state parameters c’ = 0, ’ = ’ult give a smaller force. However, this is a safe, conservative, estimate of the maximum force the soil can support. Effective Stress Analysis • For passive failure the horizontal stresses on a wall retaining dry sand are given by h g dry z N 2 c N • In this case the critical state parameters c’ = 0, ’ = ’ult give a smaller force. However, this is a safe, conservative, estimate of the maximum force the soil can support. • It is important to use effective vertical stresses, v’ = v - u to calculate the effective horizontal stresses, h’. Then the total horizontal stress is given by h = h’ - u Effective Stress Analysis • For passive failure the horizontal stresses on a wall retaining dry sand are given by h g dry z N 2 c N • In this case the critical state parameters c’ = 0, ’ = ’ult give a smaller force. However, this is a safe, conservative, estimate of the maximum force the soil can support. • It is important to use effective vertical stresses, v’ = v - u to calculate the effective horizontal stresses, h’. Then the total horizontal stress is given by h = h’ - u • If the water level is not the same on both sides of a wall, water will flow. The pore pressures must then be determined from a flow net before calculating v’. Example A 10 m high retaining wall retains 5 m of clay which overlays 3 m of sand which overlays 2 m of clay. The water table is at the surface of the retained soil. Calculate the limiting active pressure immediately after construction. 5m Clay cu = 20 kPa u = 5o gsat = 15 kN/m3 3m Sand c’ = 0 ’= 35o gsat =20kN/m3 Clay cu = 50 kPa u = 0o gsat = 15 kN/m3 2m Example - Short term analysis Layer 1: A clay layer so will be undrained in the short term. Will require a total stress (undrained) analysis Example - Short term analysis Layer 1: A clay layer so will be undrained in the short term. Will require a total stress (undrained) analysis c c u 20 kPa N 1 sin u 119 . 1 sin u Example - Short term analysis Layer 1: A clay layer so will be undrained in the short term. Will require a total stress (undrained) analysis c c u 20 kPa N 1 sin u 119 . 1 sin u Active failure thus 1 = v and 3 = h Example - Short term analysis Layer 1: A clay layer so will be undrained in the short term. Will require a total stress (undrained) analysis c c u 20 kPa N 1 sin u 119 . 1 sin u Active failure thus 1 = v and 3 = h From the Mohr-Coulomb failure criterion h v 2 cu N N v 43.6 119 . Example - Short term analysis Layer 1: A clay layer so will be undrained in the short term. Will require a total stress (undrained) analysis c c u 20 kPa N 1 sin u 119 . 1 sin u Active failure thus 1 = v and 3 = h From the Mohr-Coulomb failure criterion h v 2 cu At surface N N v 43.6 119 . z = 0, v = 0, h = - 36.6 kPa At base of layer z = 5 m, v = 5x15, h = 26.4 kPa Example - Short term analysis -36.6 z0 = 2.91 m Analysis predicts tensile stresses between the soil and the wall. These are not possible, and a tension crack may develop. 26.4 Example - Short term analysis -36.6 z0 = 2.91 m Analysis predicts tensile stresses between the soil and the wall. These are not possible, and a tension crack may develop. 26.4 Because the water table is at the surface the crack will fill with water, and a more pessimistic pressure distribution will be Example - Short term analysis -36.6 z0 = 2.91 m Analysis predicts tensile stresses between the soil and the wall. These are not possible, and a tension crack may develop. 26.4 gw z 9.81 x 2.91 26.4 Because the water table is at the surface the crack will fill with water, and a more pessimistic pressure distribution will be Example - Short term analysis Layer 2: Sand so excess pore pressures will dissipate rapidly. Cannot use total stress analysis. Example - Short term analysis Layer 2: Sand so excess pore pressures will dissipate rapidly. Cannot use total stress analysis. For sand in short term assume fully drained. Must use effective stress analysis. c c 0 N 1 sin 3.69 1 sin Example - Short term analysis Layer 2: Sand so excess pore pressures will dissipate rapidly. Cannot use total stress analysis. For sand in short term assume fully drained. Must use effective stress analysis. c c 0 N 1 sin 3.69 1 sin Active failure so ’1 = ’v and ’3 = ’h and from the Mohr-Coulomb criterion h v 2 c N N v 3.69 Example - Short term analysis Layer 2 z v u ´v = v - u ´h = ´v/3.69 u h = ´h + u 5 75 49 26 7 49 56 8 135 78.4 56.6 15.3 78.4 93.7 Example - Short term analysis Layer 2 z v u ´v = v - u ´h = ´v/3.69 u h = ´h + u 5 75 49 26 7 49 56 8 135 78.4 56.6 15.3 78.4 93.7 Note that most of horizontal pressure is due to water Example - Short term analysis Layer 3: Clay, therefore total stress (undrained) analysis for short term c c u 50 kPa N 1 sin u 1 1 sin u Example - Short term analysis Layer 3: Clay, therefore total stress (undrained) analysis for short term c c u 50 kPa N 1 sin u 1 1 sin u When u = 0 the Mohr-Coulomb criterion reduces to 1 = 3 + 2 c u Example - Short term analysis Layer 3: Clay, therefore total stress (undrained) analysis for short term c c u 50 kPa N 1 sin u 1 1 sin u When u = 0 the Mohr-Coulomb criterion reduces to 1 = 3 + 2 c u z v h 8 135 35 10 165 65 Example - Short term analysis The final pressure distribution is 2.91 28.5 26.4 2.09 56 3 93.7 35 2 65 Example - Short term analysis The final pressure distribution is 2.91 The force required to prevent active failure can be determined from the pressure diagram 2.09 F = 0.5x28.5x2.91 28.5 26.4 56 + 0.5x26.4x2.09 3 + 56x3 + 0.5x(93.7-56)x3 93.7 + 35x2 + 0.5x(65-35)x2 35 2 65 = 393.7 kN/m Example 2 A 5m high retaining wall retains a clayey soil, which overlies a highly permeable sandstone. If the water level remains at the surface of the clay in the retained soil, and is level with the top of the sandstone determine the minimum force required to maintain the stability of the wall for short and long term. The soil parameters are: c u 37 kPa , u 5o , c 0, ult 25o , g sat 19 kN / m 3 Clayey soil Sandstone 5m Example 2 - Short term Short term undrained - total stress analysis Example 2 - Short term Short term undrained - total stress analysis Minimum force for stability - active failure Example 2 - Short term Short term undrained - total stress analysis Minimum force for stability - active failure h v 2 cu N N v 67.8 119 . Example 2 - Short term Short term undrained - total stress analysis Minimum force for stability - active failure h v 2 cu N N v 67.8 119 . At surface h = - 67.8 kPa, at 5 m h = 11.9 kPa Example 2 - Short term Short term undrained - total stress analysis Minimum force for stability - active failure h v 2 cu N N v 67.8 119 . At surface h = - 67.8 kPa, at 5 m h = 11.9 kPa Allowing for tension crack filling with water, pressures acting on the wall will be zo = 4.25 m 4.25x 9.81 11.9 Example 2 - Short term Short term undrained - total stress analysis Minimum force for stability - active failure h v 2 cu N N v 67.8 119 . At surface h = - 67.8 kPa, at 5 m h = 11.9 kPa Allowing for tension crack filling with water, pressures acting on the wall will be zo = 4.25 m F 4.25x 9.81 11.9 1 1 9.81 4.252 11.9 0.75 931 . kN / m 2 2 Example 2 - Long term Long term - Effective stress analysis Pore pressures required - To be determined from a flow net Example 2 - Long term Long term - Effective stress analysis Pore pressures required - To be determined from a flow net 5m Example 2 - Long term Long term - Effective stress analysis Pore pressures required - To be determined from a flow net 5m u gw (h z) Example 2 - Long term Long term - Effective stress analysis Pore pressures required - To be determined from a flow net X 5m u gw (h z) Take datum at base of clay, then at X h = ho - Dh = 5 - (5/3)x1 = 10/3 Example 2 - Long term Long term - Effective stress analysis Pore pressures required - To be determined from a flow net X 5m u gw (h z) Take datum at base of clay, then at X h = ho - Dh = 5 - (5/3)x1 = 10/3 z = (2/3)x5 = 10/3 u=0 Example 2 - Long term Effective stress analysis with c’ = 0, ’ = 25o h v 2 c N N Now u = 0, so ’v = v = gsat z At wall base h = ’h = 38.6 kPa Hence F = 0.5 x 38.6 x 5 = 96.4 kN/m v 2.46 Coulomb’s Method Failure mechanism In Coulomb’s method a mechanism of failure has to be assumed soil movement wall movement Assumed failure plane Failure mechanism In Coulomb’s method a mechanism of failure has to be assumed soil movement wall movement Assumed failure plane If this is the failure mechanism then the Mohr-Coulomb failure criterion must be satisfied on the assumed failure planes Limit equilibrium method • The application of the failure criterion to assumed mechanisms of failure is widely used in geotechnical engineering. This is generally known as the limit equilibrium method. • It is not a rigorous theoretical method but is used because it gives simple and reasonable estimates of collapse. • The method has advantages over Rankine’s method – it can cope with any geometry – it can cope with applied loads – friction between soil and retaining walls (and other structural elements) can be accounted for Failure criterion For any point on the failure plane we have t = c + tan Failure criterion For any point on the failure plane we have t = c + tan If analysis is of undrained stability then the failure criterion must be expressed in terms of total stress using undrained parameters cu and u t = c u + tan u Failure criterion For any point on the failure plane we have t = c + tan If analysis is of undrained stability then the failure criterion must be expressed in terms of total stress using undrained parameters cu and u t = c u + tan u If the pore pressures are known or the soil is dry an effective stress analysis can be conducted and the failure criterion must be expressed in terms of effective stress and effective strength parameters c’, ’ t = c + tan Failure criterion direction of soil movement t Assumed failure plane Failure criterion direction of soil movement t Forces on the failure plane Shear Force T = t ds Assumed failure plane Failure criterion direction of soil movement t Forces on the failure plane Shear Force T = Normal Force N = t ds ds Assumed failure plane Failure criterion direction of soil movement t Forces on the failure plane Shear Force T = Normal Force N = Cohesive Force C = t ds ds c ds Assumed failure plane Failure criterion If the soil properties are constant T = C + N tan Failure criterion If the soil properties are constant T = C + N tan The forces acting on the failure plane are T N Failure criterion If the soil properties are constant T = C + N tan The forces acting on the failure plane are T N which may be more convieniently represented by C R Failure criterion For a wedge of soil failing as shown below there has to be relative movement between the wall and the soil, and the soil must be failing on this plane. soil movement wall movement Assumed failure planes Failure criterion For a wedge of soil failing as shown below there has to be relative movement between the wall and the soil, and the soil must be failing on this plane. soil movement wall movement Assumed failure planes The failure criterion between the wall and the soil may be written t = c w + tan w Failure criterion For a wedge of soil failing as shown below there has to be relative movement between the wall and the soil, and the soil must be failing on this plane. soil movement wall movement Assumed failure planes The failure criterion between the wall and the soil may be written t c w + tan w = or in terms of forces Tw = C w + N w tan w Total Stress Analysis • A total stress analysis is only valid if the soil is saturated and does not drain • In practice this generally means total stress analysis is limited to assessment of the short term stability of clayey soils • Must use total stresses and undrained parameters cu, u Total Stress Analysis H tan q dir. of soil movement H H sec q q Soil properties cu, u Soil-wall properties cw, w Total Stress Analysis - forces consistent with mechanism C2 W C1 w u R2 q R1 C 1 = c u H sec q C2 = c w H 2 W = ½ H tan q g Total Stress Analysis - polygon of forces W q C2 C1 Total Stress Analysis - polygon of forces w 90 q W q C2 C1 u Total Stress Analysis - polygon of forces w R2 R1 90 q W q C2 C1 u Total Stress Analysis - polygon of forces In the polygon of forces arrows must all be in the same direction as you move around the polygon. A check must be made that the indicated directions are consistent with the failure mechanism w R2 R1 90 q W q C2 C1 u Total Stress Analysis - polygon of forces R2 w R1 90 q u C2 W q C1 Total Stress Analysis - polygon of forces R2 w R1 90 q u Direction of R2 is not consistent with assumed mechanism. Therefore the mechanism is not valid. C2 W q C1 Total Stress Analysis - forces on the wall The polygon gives the forces acting on the soil wedge. Equal and opposite forces act on the wall. The forces acting on the wall will be Total Stress Analysis - forces on the wall The polygon gives the forces acting on the soil wedge. Equal and opposite forces act on the wall. The forces acting on the wall will be w R2 F total C2 Total Stress Analysis - forces on the wall The polygon gives the forces acting on the soil wedge. Equal and opposite forces act on the wall. The forces acting on the wall will be H w R2 F total F total C2 V Total Stress Analysis - forces on the wall The polygon gives the forces acting on the soil wedge. Equal and opposite forces act on the wall. The forces acting on the wall will be H w R2 F total F total C2 V For retaining walls the horizontal component of force is usually of most concern. For the active failure condition different values of q need to be tried to determine the maximum value of H. Total Stress Analysis - tension cracks As with Rankine’s method allowance must be made for tension cracks, and if water is present the possibility that these cracks may fill with water. Total Stress Analysis - tension cracks As with Rankine’s method allowance must be made for tension cracks, and if water is present the possibility that these cracks may fill with water. The depth, z, of the region affected by tension cracks can be determined from Rankine’s method. For active failure this gives h g z 2 cu N N 0 Total Stress Analysis - tension cracks As with Rankine’s method allowance must be made for tension cracks, and if water is present the possibility that these cracks may fill with water. The depth, z, of the region affected by tension cracks can be determined from Rankine’s method. For active failure this gives h z g z 2 cu N N = 2 cu N g 0 Total Stress Analysis - tension cracks z H q Total Stress Analysis - tension cracks W1 C2 * W2 C1 w * R2 q * R1 u * Total Stress Analysis - tension cracks If the tension cracks fill with water this has no influence on the polygon of forces. Total Stress Analysis - tension cracks If the tension cracks fill with water this has no influence on the polygon of forces. The water will provide an additional horizontal force on the wall U * R2 * C2 F total Total Stress Analysis - Example 1 V 10 o W Soil Properties dir of soil movement 5m 6.4 m 30 U o c u = 10 kPa o u = 10 c w = 2 kPa o = 20 w g = 20 kN/m 3 Total Stress Analysis - Example 1 V W Cuw Cuv W o 20 Ruw o 10 o 30 Ruv U Total Stress Analysis - Example 1 20 o Ruw = 60 kN/m 50 o 160 10 30 o 64 Effective Stress Analysis An effective stress analysis can be performed whenever the pore pressures are known. Effective Stress Analysis An effective stress analysis can be performed whenever the pore pressures are known. In practice this usually means that effective stress analysis can only be used to assess the long term stability Effective Stress Analysis An effective stress analysis can be performed whenever the pore pressures are known. In practice this usually means that effective stress analysis can only be used to assess the long term stability The failure criterion must be written in terms of effective stress, that is t = c + tan Effective Stress Analysis An effective stress analysis can be performed whenever the pore pressures are known. In practice this usually means that effective stress analysis can only be used to assess the long term stability The failure criterion must be written in terms of effective stress, that is t = c + tan In terms of forces this becomes T = C + N tan Effective Stress Analysis An effective stress analysis can be performed whenever the pore pressures are known. In practice this usually means that effective stress analysis can only be used to assess the long term stability The failure criterion must be written in terms of effective stress, that is t = c + tan In terms of forces this becomes T = C + N tan where N’ = N - U U = force due to water pressure on failure plane Effective Stress Analysis - Forces on failure plane T Failure plane N´ U Effective Stress Analysis - Forces on failure plane T Failure plane N´ U C´ Failure plane ´ R´ U Effective Stress Analysis • When performing effective stress stability calculations the critical state parameters c’ = 0, ’ = ’ult should be used • When the soil is dry the pore pressures everywhere will be zero, and the effective stresses will equal the total stresses. However, only an effective stress analysis is appropriate. • If sliding occurs between the soil and a wall appropriate effective stress failure parameters must be used. The effective parameters between any interface (eg. a wall) and the soil should be based on the ultimate conditions so that c´w = 0, ´w= ´wult Effective Stress Analysis • In using Coulomb’s method you have to assume a failure mechanism. However, this may not be the most critical (least safe) mechanism. Therefore, you need to investigate a number of mechanisms (values of q) to determine which will be the most critical. • For Active failure the Maximum force is needed (Maximum of Minimum) • For Passive failure the Minimum force is needed (Minimum of Maximum) • The most critical mechanism is unlikely to give an accurate estimate of the failure load, because observation of real soil shows failure rarely occurs on planar surfaces. Effective Stress Analysis • To select a q value for the assumed failure plane in the soil it is helpful to remember that the failure plane is inclined at an angle (p/4 - /2) to the direction of the minor principal stress 3. Effective Stress Analysis • To select a q value for the assumed failure plane in the soil it is helpful to remember that the failure plane is inclined at an angle (p/4 - /2) to the direction of the minor principal stress 3. t F 2 3 Effective Stress Analysis 3 Active Effective Stress Analysis 3 Active Passive 3 Effective Stress Analysis 3 Active Passive 3 • In the presence of steady state seepage it may be necessary to draw a flow net to determine the pore water Forces U acting on the soil wedge. Active failure W V C´uw C´uv W U uw ´w R´uw q U ´ R´uv U uv Direction of movement of soil wedge Passive failure V W R´ uw U uw W ´ w R´uv ´ C´ uw q U C´ uv U uv Effective stress analysis - Example V W X Soil Water Water m 55 m 6.4 m 30 U o 10 o W.T. Effective stress analysis - Example V W X Soil 5m 6.4 m 30 U o Effective stress analysis - Example V W X Soil 5m 6.4 m 30 U o Soil Properties c´ = 5 kPa o ´ = 10 c´ w = 2 kPa o ´ = 20 w gdry = 20 kN/m gsat = 22 kN/m 3 3 Effective stress analysis - Example V W X Soil 5m 6.4 m 30 o U C´ uv = 5 6.4 = 32 kN/m C´ uw = 2 5 = 10 kN/m Soil Properties c´ = 5 kPa o ´ = 10 c´ w = 2 kPa o ´ = 20 w gdry = 20 kN/m gsat = 22 kN/m 3 3 Effective stress analysis - Example V W X Soil 5m 6.4 m 30 o Soil Properties c´ = 5 kPa o ´ = 10 c´ w = 2 kPa o ´ = 20 w gdry = 20 kN/m gsat = 22 kN/m 3 3 U C´ uv = 5 6.4 = 32 kN/m C´ uw = 2 5 = 10 kN/m W = 0.5 5 2.89 22 + (8 - 0.5 5 2.89) 20 = 174.5 kN/m Example - Water pressures on soil wedge V W X U u 5 9.81 Example - Water pressures on soil wedge V W X U u 5 9.81 U uv 0.5 5 9.81 5.77 1415 . kN / m U uw 0.5 5 9.81 5 122.5 kN / m Example - Forces on soil wedge C´uw Uuw W C´uv R´uw Uuv R´uv Example - Polygon of forces Cúw Uuw R´uw W Cúv Uuv U uw R´uv U uv 60 o C´ uw W 30 o C´ uv Example - Polygon of forces Cúw Uuw R´uw W Cúv Uuv U uw 60 o R´uv U uv 60 o C´ uw W 30 o C´ uv Example - Polygon of forces o 20 Cúw Uuw R´uw W Cúv Uuv Uuw o 60 R´uv Uuv o 60 C´ uw W o 30 C´ uv Example - Forces on the wall R´uw U uw C´uw Example - Forces on the wall R´uw U uw C´uw The vertical and horizontal components of the force on the wall are Vertical T uw = R´ uw sin ´ w + C´ uw = 5.8 + 10 = 15.8 kN/m Example - Forces on the wall R´uw U uw C´uw The vertical and horizontal components of the force on the wall are Vertical T uw = R´ uw sin ´ w + C´ uw = 5.8 + 10 = 15.8 kN/m Horizontal N uw = R´ uw cos ´ w + U uw = 15.97 + 122.5 = 138.5 kN/m Example - Forces on the wall R´uw U uw C´uw The vertical and horizontal components of the force on the wall are Vertical T uw = R´ uw sin ´ w + C´ uw = 5.8 + 10 = 15.8 kN/m Horizontal N uw = R´ uw cos ´ w + U uw = 15.97 + 122.5 = 138.5 kN/m Note that N uw is largely due to water pressure. However, due to water on the other side of the wall the net resistance required for stability is only 15.97 kN/m Example 3 Example 3 uD g w ( hD zD ) Example 3 uD g w ( hD zD ) Choosing a local datum at E: hD = 0 Example 3 x uD g w ( hD zD ) Choosing a local datum at E: hD = 0, zD = - x and uD = + gw x Example 3 The pore pressure at several points along the failure plane needs to be determined to evaluate the force due to the water pressures. Example 3 The pore pressure at several points along the failure plane needs to be determined to evaluate the force due to the water pressures. The forces on the assumed failing soil wedge are then W 2 U w = 0.5 g w H w ´ cs U From flow net ´ w R´ R´ w K a tg 2 450 2 K p tg 2 450 2 AÙp löïc chuû ñoäng vaø bò ñoäng cuûa ñaát rôøi Thay ñoåi tyû soá aùp löïc ñaát ngang vaø ñöùng theo bieán daïng ngang trong thí nghieäm neùn ba truïc K a tg 2 450 2 K p tg 2 450 2 Heä soá aùp löïc ñaát trong tröôøng hôïp maët ñaát nghieâng Heä soá aùp löïc ñaát trong tröøong hôïp löng töôøng nhaùm Aùp löïc chuû ñoäng vaø bò ñoäng theo lyù thuyeát Coulomb Ka Kp sin 2 sin sin sin 2 sin 1 sin sin sin 2 2 sin sin sin 2 sin 1 sin sin 2 Phöông phaùp veõ Culmann Aùp löïc ñaát theo lyù thuyeát Rankine Toång aùp löïc taùc ñoäng leân töôøng F = ½ (gw +Ka g’)H2 Caùc phöông phaùp thöôøng söû duïng Tröøong hôïp coù nöôùc chaûy Töôøng baûn coù doøng nöôùc Xeùt taûi troïng ñoäng Ea [1 / 2]g H 2 (1 kv ) K a cos 2 ( q ) Ka sin( ) cos( q ) cos q cos 2 cos( q ) 1 cos( q ) cos( ) kh 1 k v q arctg Ñaøo töôøng ñuùc beâ toâng taïi choå Chuyeån vò töôøng vaø traïng thaùi giôùi haïn cuûa ñaát Traïng thaùi moment trong caùc giai ñoaïn thi coâng Aùp löïc ñaát coù xeùt ñeán söï ñaàm chaët ñaát treân maët HEÄ SOÁ AN TOAØN CHOÁNG TUOÄT 2leg z tg a 2le tg a FS p g zK a SV S H K a SV S H HEÄ SOÁ AN TOAØN CHOÁNG ÑÖÙT FSb t f y g HK a SV S H THÍ DUÏ: moät töôøng chaén cao 8m. Ñaát ñaép sau löng töôøng coù g = 16,6 KN/m2; = 300. Theùp Galvani ñöôïc söû duïng ñeå xaây töôøng chaén.Tính heä gia cöôøng vôùi FS9p) = FS(B) = 3 Caùc ñaëc tröng khaùc a = 200 vaø löïc chòu keùo cuûa theùp fy = 2,4105 KN/m2. GIAÛI: Choïn SV = 0,5m; SH = 1m; maët thanh theùp = 75mm. Töø = 300 Ka = 1/3 Tmax = gHKaSVSH =16,6 8 (1/3) 0,5 1 = 22,14 KN Beà daày taám theùp g HK a S v S H FSb 22,14 3 t 0,00369m 5 fy 0,075 2,4 10 Neáu theùp coù ñoä ró seùt 0,025mm/naêm vaø tuoåi thoï coâng trình laø 50 naêm Chieàu daày caàn thieát cuûa thanh theùp laø 3,69+0,025 50= 4,94mm choïn t= 5mm CHIEÀU DAØI CAÀN THIEÁT THANH GIA CÖÔØNG 0 FS p K a SV S H L H tg 45 13,78m 2 2 tg a Slide 29 of 36 Slide 23 of 36 Slide 24 of 36 Slide 25 of 36 Slide 26 of 36 Slide 27 of 36 Slide 28 of 36