Download Equivalent Algebraic Equations

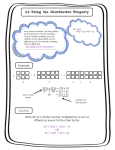
Equivalent Algebraic
Equations
•
•
•
•
•
Learn and use the distributive property
Rewrite equations to determine whether they
are equivalent
Formalize algebraic properties
Identify properties as they are used in solving
equations
Introduce factoring as a reverse of the
distributive property
 In the previous lesson you learned to write
the equation of line using the point-slope
form. You were given the slope and a
point.
 But remember that a line goes through
many points. Will the equation be
equivalent if it written using another point?
 In this lesson you will learn how to identify
different equations that describe the same
line.
 If a line with slope 2
that passes through
the point (-4,3) can
be described by the
equation y = 3 +
2(x+4).
 This line also passes
through (1, 13), so
it can also be
described by the
equation
y=13+2(x-1).
 If we place both of these equations in Y1
and Y2 in our graphing calculator, we see
they produce the same line when graphed.
 When a table is produced you can see that
the same set of values is produced.
 There are many equivalent equations that
can be used to describe a given line.
The Distributive
Property








Place the Distributive
Property Template in your
Communicator®.
Let’s picture 2(7) on grid
paper.
One way to describe its
area is to say it is 2(4+3).
Another way is to think of
it as 2(4) + 2(3), by
separating the rectangle
into two parts.
Notice that 2(7)=2(4+3)=
2(4)+2(3)=14
This is called the
distributive property.
Model another distributive
property on the grid paper
Write the distributive
property on your
Communicator®
The Distributive
Property








Place the Distributive
Property Template in your
Communicator®.
Let’s picture 2(x+4) on the
multiplication rectangle.
Place 2 units on the left.
Place x + 4 across the top.
Fill in the multiplication.
We see that another way is
to think of2(x+4) is 2(x) +
2(4).
This is called the
distributive property.
Model another 3(x-1) on
the multiplication
rectangle.
Write the distributive
property on your
Communicator®
 We can use the distributive property to






rewrite some of our equations.
Suppose y = 3 + 2(x + 4).
Using the distributive property gives us
y=3 + 2(x) + 2(4) or y = 3 + 2x + 8
Or this can be rewritten as y = 11 + 2x.
Point Slope form: y = 3 + 2(x+4)
Slope Intercept form: y = 11 + 2x.
Describe what each tells us.
 Complete steps 1-5 with your group. Be
prepared to explain your thinking on each
step.
a.
b.
c.
d.
e.
f.
y
y
y
y
y
y
=
=
=
=
=
=
3 - 2(x - 1)
-5 - 2(x - 5)
9 - 2(x + 2)
0 - 2(x - 2.5)
7 - 2(x + 1)
-9 - 2(x - 7)
 Complete steps 6-7 with your group.
a.
b.
c.
d.
e.
f.
g.
y = 2(x-2.5)
y=18+2(x-8)
y=52-6(x+8)
y=-6+2(x+4)
y=21-6(x+4)
y=-14-6(x-3)
y=-10+2(x+6)
h. 6x+y = 4
i. y=11+2(x-8)
j. 12x + 2y=-6
k. y=2(x-4)+10
l. y=15-2(10-x)
m. y=7+2(x-6)
n. y=-6(x+0.5)
o. y=-6(x+2)+16
Writing equation in different
forms
 Intercept Form:
 Point-Slope Form:
y = a + bx
y = y1 + b(x - x1)
 An equation of the form ax + by = c are
said to be in standard form
Properties of Arithmetic
 Distributive Property
 Commutative Property of Addition
 Commutative Property of Multiplication
 Associative Property of Addition
 Associative Property of Multiplication
Properties of Equality
 Given that a = b, for any number c
 a+c=b+c
Addition Property of Equality
 a-c=b-c
Subtraction Property of Equality
 ac=bc
Multiplication Property of Equality
 a/c =b/c (c≠0) Division Property of Equality
Show two equations are
equivalent
 y = 2 + 3(x - 1)
 Original Equation
 y = 2 + 2x - 3
 Distributive
 y = -1 + 3x
Property
 Combine Like
Terms
So y = 2 + 3(x - 1) is
equivalent to the equation
y = -1 + 3x.
Show two equations are
equivalent
 6x -2y = 2
 -2y = 2 - 6x
 Original Equation
 Subtraction Property
 y = (2 - 6x)/-2
 y = -1 + 3x
 Division Property
 Distributive Property
So 6x – 2y = 2 is equivalent to
the equation y = -1+3x.
Checking for Equivalency
 You can enter the intercept form and the
point-slope form in the calculator to verify
they are equivalent.
 The Standard Form (ax + by = c) cannot
be entered in the calculator for verification.
 By using properties of equality solve the
equation
3x  4
5  7
6
 Identify the properties you use on each
step.