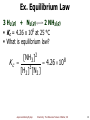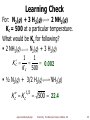* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download wiley_ch6_Chemical_Equilibrium
Condensed matter physics wikipedia , lookup
Drug discovery wikipedia , lookup
Lewis acid catalysis wikipedia , lookup
Multi-state modeling of biomolecules wikipedia , lookup
Thermomechanical analysis wikipedia , lookup
California Green Chemistry Initiative wikipedia , lookup
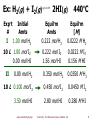
Colloidal crystal wikipedia , lookup
Freshwater environmental quality parameters wikipedia , lookup
Chemical reaction wikipedia , lookup
Nuclear chemistry wikipedia , lookup
Size-exclusion chromatography wikipedia , lookup
Institute of Chemistry Ceylon wikipedia , lookup
Pseudo Jahn–Teller effect wikipedia , lookup
History of chemistry wikipedia , lookup
Inorganic chemistry wikipedia , lookup
Process chemistry wikipedia , lookup
Analytical chemistry wikipedia , lookup
Molecular dynamics wikipedia , lookup
Thermodynamics wikipedia , lookup
Thermodynamic equilibrium wikipedia , lookup
Stability constants of complexes wikipedia , lookup
Chemical thermodynamics wikipedia , lookup
George S. Hammond wikipedia , lookup
Rate equation wikipedia , lookup
Green chemistry wikipedia , lookup
Click chemistry wikipedia , lookup
Bioorthogonal chemistry wikipedia , lookup
Stoichiometry wikipedia , lookup
Computational chemistry wikipedia , lookup
Physical organic chemistry wikipedia , lookup
Transition state theory wikipedia , lookup
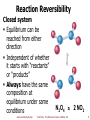
Chapter 6 Chemical Equilibrium Chemistry: The Molecular Nature of Matter, 6E Jespersen/Brady/Hyslop Dynamic Equilibrium in Chemical Systems Chemical equilibrium exists when Rates of forward and reverse reactions are equal Reaction appears to stop [reactants] and [products] don't change over time Remain constant Both forward and reverse reaction never cease Equilibrium signified by double arrows ( or equal sign (=) Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E ) 2 Dynamic Equilibrium N2O4 2 NO2 Initially forward reaction rapid As some reacts [N2O4] so rate forward Initially Reverse reaction slow No products As NO2 forms Reverse rate Ions collide more frequently as [ions] Eventually rateforward = ratereverse Equilibrium Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 3 Dynamic Equilibrium (Fig. 15.1) Almost all systems come to equilibrium Where equilibrium lies depends on system Some systems’ equilibrium hard to detect Essentially no reactants or no products present Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 4 Reaction Reversibility Closed system Equilibrium can be reached from either direction Independent of whether it starts with “reactants” or “products” Always have the same composition at equilibrium under same conditions Jespersen/Brady/Hyslop N 2O 4 Chemistry: The Molecular Nature of Matter, 6E 2 NO2 5 Reactants Equilibrium N2O4 Products 2 NO2 For given overall system composition Always reach same equilibrium concentrations Whether equilibrium is approached from forward or reverse direction Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 6 Equilibrium Simple relationship among [reactants] and [products] for any chemical system at equilibrium Called = mass action expression Derived from thermodynamics Forward reaction: A B k Reverse reaction: A B At equilibrium: A B kf r rate forward = rate reverse rearranging: Jespersen/Brady/Hyslop Rate = kf[A] Rate = kr[B] kf[A] = kr[B] [B] k f constant [A] k r Chemistry: The Molecular Nature of Matter, 6E 7 Ex: H2(g) + I2(g) 2HI(g) 440°C Exp’t Initial # Amts I 1.00 mol H2 Equil’m Amts 0.222 mol H2 Equil’m [M] 0.0222 M H2 10 L 1.00 mol I2 0.00 mol HI 0.222 mol I2 1.56 mol HI 0.0222 M I2 0.156 M HI 0.00 mol H2 0.350 mol H2 0.0350 M H2 10 L 0.100 mol I2 0.450 mol I2 0.0450 M I2 3.50 mol HI 2.80 mol HI 0.280 M HI II Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 8 Ex: H2(g) + I2(g) Exp’t Initial Amts # 2HI(g) 440°C Equil’m Amts Equil’m [M] III 0.0150 mol H2 0.150 mol H2 0.0150 M H2 10 L 0.00 mol I2 0.135 mol I2 0.0135 M I2 1.27 mol HI 1.00 mol HI 0.100 M HI IV 0.00 mol H2 0.442 mol H2 0.0442 M H2 10 L 0.00 mol I2 0.442 mol I2 0.0442 M I2 4.00 mol HI 3.11 mol HI 0.311 M HI Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 9 Mass Action Expression (MAE) Uses stoichiometric coefficients as exponent for each reactant For reaction: aA + bB cC + dD c d [C] [D] Q b a [A] [B] Reaction quotient Numerical value of mass action expression Equals “Q” at any time, and Equals “K” only when reaction is known to be at equilibrium Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 10 Mass Action Expression 2 [HI] Q = same for all data sets at equilibrium [H2 ][I 2 ] Equilibrium Concentrations (M) Exp’t [H2] [I2] [HI] I 0.0222 0.0222 0.156 II 0.0350 0.0450 0.280 III 0.0150 0.0135 0.100 IV 0.0442 0.0442 0.311 [HI]2 Q [H2 ][I 2 ] (0.156 )2 49.4 (0.0222 )(0.0222 ) (0.280 )2 49.8 (0.0350 )(0.0450 ) (0.100 )2 49.4 (0.0150 )(0.0135 ) (0.311)2 49.5 (0.0442 )(0.0442 ) Average = 49.5 Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 11 Equilibrium Law For reaction at equilibrium write the following Equilibrium Law (at 440 °C) Kc 2 [HI] 49.5 [H2 ][I 2 ] Equilibrium constant = Kc = constant at given T Use Kc since usually working with concentrations in mol/L For chemical equilibrium to exist in reaction mixture, reaction quotient Q must be equal to equilibrium constant, Kc Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 12 Predicting Equilibrium Law For general chemical reaction: dD + eE fF + gG Where D, E, F, and G represent chemical formulas d, e, f, and g are coefficients f Mass action expression = [F] [G] g [D]d [E]e Note: Exponents in mass action expression are stoichiometric coefficients in balanced equation. [F] f [G]g K c Equilibrium law is: [D]d [E]e Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 13 Ex. Equilibrium Law 3 H2(g) + N2(g) 2 NH3(g) Kc = 4.26 x 108 at 25 °C What is equilibrium law? Kc [NH3 ] 3 2 [H2 ] [N 2 ] Jespersen/Brady/Hyslop 4.26 10 8 Chemistry: The Molecular Nature of Matter, 6E 14 Learning Check Write mass action expressions for the following: 2 NO2 (g) N2O4 (g) [N2O4] Q 2 [NO2] 2CO (g) + O2 (g) 2 CO2 (g) 2 [CO2] Q 2 [CO] [O2] Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 15 Your Turn! Which of the following is the correct mass action expression (MAE) for the reaction: Cu2+(aq) + 4NH3(aq) [Cu(NH3)42+](aq)? A. B. C. Q [Cu(NH3 ) 24 ] [Cu2 ][NH3 ]4 Q [Cu(NH3 ) 24 ] Q [Cu2 ][NH3 ]4 [Cu2 ][NH3 ] [Cu(NH3 ) 24 ] D. none of these Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 16 Manipulating Equations for Chemical Equilibria Various operations can be performed on equilibrium expressions 1. When direction of equation is reversed, new equilibrium constant is reciprocal of original [C][D] Kc A+B C+D [A][B] C +D A+B Jespersen/Brady/Hyslop [A][B] 1 K c [C][D] K c Chemistry: The Molecular Nature of Matter, 6E 17 Ex. Manipulating Equilibria 1 1. When direction of equation is reversed, new equilibrium constant is reciprocal of original 3 H2(g) + N2(g) Kc [NH3 ] [H2 ]3 [N 2 ] 2 NH3(g) K c 2 4.26 10 at 25°C 8 3 H2(g) + N2(g) 3 [H2 ] [N2 ] [NH3 ] 2 NH3(g) 2 Jespersen/Brady/Hyslop 1 Kc 1 4.26 10 8 at 25°C 2.35 10 Chemistry: The Molecular Nature of Matter, 6E 9 18 Manipulating Equilibria 2 2. When coefficients in equation are multiplied by a factor, equilibrium constant is raised to a power equal to that factor. A+B 3A + 3B K c Kc C+D 3 [C][D] [A][B] 3C + 3D 3 [C] [D] [A]3 [B] 3 [C][D] [C][D] [C][D] 3 Kc [A][B] [A][B] [A][B] Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 19 Manipulating Equilibria 2 2. When coefficients in equation are multiplied by factor, equilibrium constant is raised to power equal to that factor 3 H2(g) + N2(g) 2 NH3(g) at 25°C Kc [NH3 ] 2 4.26 10 8 [H2 ]3 [N 2 ] multiply by 3 9 H2(g) + 3 N2(g) 6 NH3(g) K c [NH3 ]6 9 [H2 ] [N 2 ] Jespersen/Brady/Hyslop 3 3 Kc Chemistry: The Molecular Nature of Matter, 6E 20 Manipulating Equilibria 3 3. When chemical equilibria are added, their equilibrium constants are multiplied [C ][D ] A+B C + D Kc 1 [A ][B ] C+E [F ][G ] K c2 [C ][E ] D+F+G F+G A+B+E [C ][D ] [F ][G ] [D ][F ][G ] K c3 K c1 K c 2 [A ][B ] [C ][E ] [A ][B ][E ] Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 21 Manipulating Equilibria 3 3. When chemical equilibria are added, their equilibrium constants are multiplied 2 NO2(g) NO3(g) + NO(g) NO3(g) + CO(g) NO2(g) + CO2(g) NO2(g) + CO(g) NO(g) + CO2(g) [NO][NO 3 ] K c1 [NO][NO3 ] [NO 2 ]2 K c2 [NO2 ][CO2 ] [NO3 ][CO] K c3 [NO][CO2 ] [NO 2 ][CO] [NO 2 ][CO 2 ] [NO][CO2 ] [NO2 ][CO] [NO 3 ][CO] [NO 2 ]2 K c1 K c 2 K c 3 Therefore Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 22 Learning Check For: N2(g) + 3 H2(g) 2 NH3(g) Kc = 500 at a particular temperature. What would be Kc for following? 2 NH3(g) N2(g) + 3 H2(g) K c 1 Kc 1 0.002 500 ½ N2(g) + 3/2 H2(g) K c K c 12 NH3(g) 500 22.4 Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 23 Equilibrium Constant, Kc Constant value equal to ratio of product concentrations to reactant concentrations raised to their respective exponents [products]f Kc d [reactants ] Changes with temperature (van’t Hoff Equation) Depends on solution concentrations Assumes reactants and products are in solution Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 24 Equilibrium Constant, Kp Based on reactions in which substances are gaseous Assumes gas quantities are expressed in atmospheres in mass action expression Use partial pressures for each gas in place of concentrations Ex. N2 (g) + 3 H2 (g) 2 NH3 (g) KP Jespersen/Brady/Hyslop 2 PNH 3 PN2 PH3 2 Chemistry: The Molecular Nature of Matter, 6E 25 How are Kp and Kc Related? Start with Ideal Gas Law PV=nRT Rearranging gives n P RT MRT V Substituting P/RT for molar concentration into Kc results in pressure-based formula ∆n = moles of gas in product – moles of gas in reactant Kp Kc (RT )n Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 26 Learning Check Consider the reaction: 2NO2(g) N2O4(g) If Kp = 0.480 for the reaction at 25°C, what is value of Kc at same temperature? n = nproducts – nreactants = 1 – 2 = –1 Δn Kp Kc(RT) Kc Kp (RT) Kc = 11.7 n Jespersen/Brady/Hyslop 0.480 (0.0821 298K ) Chemistry: The Molecular Nature of Matter, 6E 1 27 Your Turn! Consider the reaction A(g) + 2B(g) 4C(g) If the Kc for the reaction is 0.99 at 25ºC, what would be the Kp? A. 0.99 Δn=(4 – 3)=1 B. 2.0 C. 24. Kp = Kc(RT)Δn Kp= 0.99*(0.082057*298.15)1 D. 2400 Kp = 24 E. None of these Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 28 Homogeneous reaction/equilibrium All reactants and products in same phase Can mix freely Heterogeneous reaction/equilibrium Reactants and products in different phases Can’t mix freely Solutions are expressed in M Gases are expressed in M Governed by Kc Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 29 Heterogeneous Equilibria 2NaHCO3(s) Na2CO3(s) + H2O(g) + CO2(g) Equilibrium Law = [Na 2CO 3 (s )][H 2O ( g )][CO 2 ( g )] K [NaHCO 3 (s )]2 Can write in simpler form For any pure liquid or solid, ratio of moles to volume of substance (M) is constant Ex. 1 mol NaHCO3 occupies 38.9 cm3 2 mol NaHCO3 occupies 77.8 cm3 M 1 mol NaHCO3 M 25.7M 0.0389 L Jespersen/Brady/Hyslop 2 mol NaHCO3 25.7M 0.0778 L Chemistry: The Molecular Nature of Matter, 6E 30 Heterogeneous Equilibria 2NaHCO3(s) Na2CO3(s) + H2O(g) + CO2(g) Ratio (n/V) or M of NaHCO3 is constant (25.7 mol/L) regardless of sample size Likewise can show that molar concentration of Na2CO3 solid is constant regardless of sample size So concentrations of pure solids and liquids can be incorporated into equilibrium constant, Kc [Na2 CO3 (s )] Kc K [H2 O( g )][CO2 ( g )] 2 [NaHCO3 (s )] Equilibrium law for heterogeneous system written without concentrations of pure solids or liquids Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 31 Interpreting KC Large K (K>>1) Means product rich mixture Reaction goes far toward completion Ex. 2SO2(g) + O2(g) 2SO3(g) Kc = 7.0 1025 at 25 ° C Kc [SO 3 ] 2 7.0 10 2 1 [SO 2 ] [O 2 ] Jespersen/Brady/Hyslop 25 Chemistry: The Molecular Nature of Matter, 6E 32 Interpreting KC Small K (K<<1) Means reactant rich mixture Only very small amounts of product formed Ex. H2(g) + Br2(g) 2HBr(g) Kc = 1.4 10–21 at 25 °C 2 21 [HBr] 1.4 10 Kc [H2 ][Br2 ] 1 Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 33 Interpreting KC K 1 Means product and reactant concentrations close to equal Reaction goes only ~ halfway Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 34 Size of K gives measure of how reaction proceeds K >> 1 K=1 K << 1 [products] >> [reactants] [products] = [reactants] [products] << [reactants] Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 35 Learning Check Consider the reaction of 2NO2(g) N2O4(g) If Kp = 0.480 at 25°C, does the reaction favor product or reactant? K is small (K < 1) Reaction favors reactant Since K is close to 1, significant amounts of both reactant and product are present Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 36 Equilibrium Positions and “Shifts” Equilibrium positions Combination of concentrations that allow Q = K Infinite number of possible equilibrium positions Le Châtelier’s principle System at equilibrium (Q = K) when upset by disturbance (Q ≠ K) will shift to offset stress System said to “shift to right” when forward reaction is dominant (Q < K) System said to “shift to left” when reverse direction is dominant (Q > K) Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 37 Relationship Between Q and K Q=K Q<K reaction at equilibrium reactants products Too many reactants Must convert some reactant to product to move reaction toward equilibrium Q>K reactants products Too many products Must convert some product to reactant to move reaction toward equilibrium Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 38 Examples of Le Châtelier’s Principle Let’s see how this works with changes in 1. Concentration 2. Pressure and volume 3. Temperature 4. Catalysts 5. Adding inert gas to system at constant volume Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 39 Effect of Change in Concentration 2SO2(g) + O2(g) → 2SO3(g) Kc = 2.4 x 10-3 at 700 oC Which direction will the reaction move if 0.125 moles of O2 is added to an equilibrium mixture ? A. Towards the products B. Towards the reactants C. No change will occur Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 40 Effect of Change in Concentration When changing concentrations of reactants or products Equilibrium shifts to remove reactants or products that have been added Equilibrium shifts to replace reactants or products that have been removed Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 41 Effect of Pressure and Volume Changes Consider gaseous system at constant T and n 2 3H2(g) + N2(g) 2NH3(g) PNH 3 K P If reduce volume (V) PN2 PH3 2 Expect Pressure to increase (P) To reduce pressure, look at each side of reaction Which has less moles of gas Reactants = 3 + 1 = 4 moles gas Products = 2 moles gas Reaction favors products (shifts to right) Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 42 Effect of P and V Changes Consider gaseous system at constant T and n Ex. H2(g) + I2(g) 2 HI(g) 2 PHI KP PH2 PI2 If pressure is increased, what is the effect on equilibrium? nreactant = 1 + 1 = 2 nproduct = 2 Predict no change or shift in equilibrium Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 43 Effect of P and V Changes 2NaHSO3(s) NaSO3(s) + H2O(g) + SO2(g) K P PH2OPSO2 If you decrease volume of reaction, what is the effect on equilibrium? Reactants: no moles gas = all solids Products: 2 moles gas V, causes P Reaction shifts to left (reactants), as this has fewer moles of gas Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 44 Effect of P and V Changes Reducing volume of gaseous reaction mixture causes reaction to decrease number of molecules of gas, if it can Increasing pressure Moderate pressure changes have negligible effect on reactions involving only liquids and/or solids Substances are already almost incompressible Changes in V, P and [X] effect position of equilibrium (Q), but not K Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 45 Effect of Temperature Changes H2O(s) H° =+6 kJ (at 0 °C) H2O(ℓ) Energy + H2O(s) H2O(ℓ) Energy is reactant Add heat, shift reaction right 3H2(g) + N2(g) 3 H2(g) + N2(g) 2NH3(g) Hf°= –47.19 kJ 2 NH3(g) + energy Energy is product Add heat, shift reaction left Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 46 Effect of Temperature Changes T shifts reaction in direction that produces endothermic (heat absorbing) change T shifts reaction in direction that produces exothermic (heat releasing) change Changes in T change value of mass action expression at equilibrium, so K changed K depends on T T of exothermic reaction makes K smaller More heat (product) forces equilibrium to reactants T of endothermic reaction makes K larger More heat (reactant) forces equilibrium to products Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 47 Catalysts And Equilibrium Catalyst lowers Ea for both forward and reverse reaction Change in Ea affects rates kr and kf equally Catalysts have no effect on equilibrium Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 48 Effect of Adding Inert Gas Inert gas One that does not react with components of reaction Ex. Argon, Helium, Neon, usually N2 Adding inert gas to reaction at fixed V (n and T), P of all reactants and products Since it doesn’t react with anything No change in concentrations of reactants or products No net effect on reaction Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 49 Your Turn! The following are equilibrium constants for the reaction of acids in water, Ka. Which is the most efficient reaction? A. Ka = 2.2×10–3 B. Ka = 1.8×10–5 C. Ka = 4.0×10–10 D. Ka = 6.3×10–3 Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 50 Equilibrium Calculations For gaseous reactions, use either KP or KC For solution reactions, must use KC Either way, two basic categories of calculations 1. Calculate K from known equilibrium concentrations or partial pressures 2. Calculate one or more equilibrium concentrations or partial pressures using known KP or KC Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 51 Calculating KC from Equilibrium Concentrations When all concentrations at equilibrium are known Use mass action expression to relate concentrations to KC Two common types of calculations A. Given equilibrium concentrations, calculate K B. Given initial concentrations and one final concentration Calculate equilibrium concentration of all other species Then calculate K Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 52 Calculating KC Given Equilibrium Concentrations Ex. 1 N2O4(g) 2NO2(g) If you place 0.0350 mol N2O4 in 1 L flask at equilibrium, what is KC? [N2O4]eq = 0.0292 M [NO2]eq = 0.0116 M 2 [NO 2 ] Kc [N 2O 4 ] 2 [0.0116] Kc [0.0292] KC = 4.61 10–3 Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 53 Your Turn! For the reaction: 2A(aq) + B(aq) 3C(aq) the equilibrium concentrations are: A = 2.0 M, B = 1.0 M and C = 3.0 M. What is the expected value of Kc at this temperature? A. 14 [C]3 Kc 2 B. 0.15 [A] [B] C. 1.5 [3.0]3 D. 6.75 Kc 2 [2.0] [1.0] Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 54 Calculating KC Given Initial Concentrations and One Final Concentration Ex. 2 2SO2(g) + O2(g) 2SO3(g) 1.000 mol SO2 and 1.000 mol O2 are placed in a 1.000 L flask at 1000 K. At equilibrium 0.925 mol SO3 has formed. Calculate KC for this reaction. 1st calculate concentrations of each Initial 1.00mol [SO 2 ] [O 2 ] 1.00M 1.00L Equilibrium 0.925mol [SO 3 ] 0.925M 1.00L Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 55 How to Solve: Set up Concentration Table Based on the following: Changes in concentration must be in same ratio as coefficients of balanced equation Set up table under balanced chemical equation Initial concentrations Controlled by person running experiment Changes in concentrations Controlled by stoichiometry of reaction Equilibrium concentrations Equilibrium Change in Initial = – Concentration Concentration Concentration Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 56 Next Set up Concentration Table 2SO2(g) + O2(g) Initial Conc. (M) 1.000 Changes in Conc. (M) –0.925 Equilibrium Conc. (M) 0.075 1.000 –0.462 0.538 2SO3(g) 0.000 +0.925 0.925 [SO2] consumed = Amt of SO3 formed = [SO3] at equilibrium = 0.925 M [O2] consumed = ½ amt SO3 formed = 0.925/2 = 0.462 M [SO2] at equilibrium = 1.000 – 0.975 = 0.075 [O2] at equilibrium = 1.00 – 0.462 = 0.538 M Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 57 Ex. 2 Finally calculate KC at 1000 K Kc Kc [SO 3 ]2 [SO 2 ]2 [O 2 ] 2 [0.925] 2 [0.075] [0.538] Kc = 2.8 × 102 = 280 Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 58 Summary of Concentration Table Used for most equilibrium calculations (Ch 15, 17, and 18) 1. Equilibrium concentrations are only values used in mass action expression Values in last row of table 2. Initial value in table must be in units of mol/L (M) [X]initial = those present when reaction prepared No reaction occurs until everything is mixed Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 59 Summary of Concentration Table 3. Changes in concentrations always occur in same ratio as coefficients in balanced equation 4. In “change” row be sure all [reactants] change in same directions and all [products] change in opposite direction. If [reactant]initial = 0, its change must be + () because [reactant]final negative If [reactants] , all entries for reactants in change row should have minus sign and all entries for products should be positive Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 60 Calculate [X]equilibrium from Kc and [X]initial When all concentrations but one are known Use mass action expression to relate Kc and known concentrations to obtain missing concentrations Ex. 3 CH4(g) + H2O(g) CO(g) + 3H2(g) At 1500 °C, Kc = 5.67. An equilibrium mixture of gases had the following concentrations: [CH4] = 0.400 M and [H2] = 0.800M and [CO] =0.300M. What is [H2O] at equilibrium ? Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 61 Calculate [X]equilibrium from Kc and [X]initial Ex. 3 CH4(g) + H2O(g) CO(g) + 3H2(g) Kc = 5.67 [CH4] = 0.400 M; [H2] = 0.800M; [CO] =0.300M What is [H2O] at equilibrium? First, set up equilibrium 3 [CO][H2 ]3 [H2O] [CH4 ]K c [CO][H2 ] Kc [CH4 ][H2O] Next, plug in equilibrium concentrations and Kc [0.300][0. 800]3 0.154 [H2O] [0.400](5.67) 2.27 [H2O] = 0.0678 M Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 62 Calculating [X]Equilibrium from Kc When Initial Concentrations Are Given Write equilibrium law/mass action expression Set up Concentration table Allow reaction to proceed as expected, using “x” to represent change in concentration Substitute equilibrium terms from table into mass action expression and solve Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 63 Calculate [X]equilibrium from [X]initial and KC Ex. 4 H2(g) + I2(g) 2HI(g) at 425 °C KC = 55.64 If one mole each of H2 and I2 are placed in a 0.500 L flask at 425 °C, what are the equilibrium concentrations of H2, I2 and HI? Step 1. Write Equilibrium Law 2 [HI ] Kc 55.64 [H 2 ][I 2 ] Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 64 Ex. 4 Step 2. Concentration Table Conc (M) H2(g) + I2(g) 2HI (g) Initial Change Equil’m 2.00 2.00 0.000 –x –x +2x +2x 2.00 – x 2.00 – x Initial [H2] = [I2] = 1.00 mol/0.500L =2.00M Amt of H2 consumed = Amt of I2 consumed = x Amt of HI formed = 2x (2x ) 2 (2x ) 2 55.64 (2.00 x )(2.00 x ) (2.00 x ) 2 Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 65 Ex. 4 Step 3. Solve for x Both sides are squared so we can take square root of both sides to simplify (2x ) 2 K 55.64 (2.00 x ) 2 2x 7.459 (2.00 x ) 7.459(2.00 x ) 2x 14.918 7.459x 2x 14.918 9.459x 14.918 x 1.58 9.459 Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 66 Ex. 4 Step 4. Equilibrium Concentrations Conc (M) H2(g) + Initial 2.00 Change – 1.58 Equil’m 0.42 I2(g) 2.00 – 1.58 0.42 2HI (g) 0.00 +3.16 +3.16 [H2]equil = [I2]equil = 2.00 – 1.58 = 0.42 M [HI]equil = 2x = 2(1.58) = 3.16 Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 67 Calculate [X]equilibrium from [X]initial and KC Ex. 5 H2(g) + I2(g) 2HI(g) at 425 °C KC = 55.64 If one mole each of H2, I2 and HI are placed in a 0.500 L flask at 425 °C, what are the equilibrium concentrations of H2, I2 and HI? Now have product as well as reactants initially Step 1. Write Equilibrium Law 2 [HI ] Kc 55.64 [H 2 ][I 2 ] Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 68 Ex. 5 Step 2. Concentration Table Conc (M) H2(g) + I2(g) 2HI (g) Initial Change Equil’m 2.00 2.00 2.00 –x –x 2.00 – x 2.00 – x +2x 2.00 + 2x (2.00 2x ) 2 (2.00 2x ) 2 55.64 (2.00 x )(2.00 x ) (2.00 x ) 2 K 55.64 (2.00 2x ) 2 (2.00 x ) 2 Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 69 Ex. 5 Step 3. Solve for x 2.00 2x 7.459 (2.00 x ) 7.459(2.00 x ) 2.00 2x 14.918 7.459x 2.00 2x 12.918 9.459 x 12.918 x 1.37 9.459 Jespersen/Brady/Hyslop [H2]equil = [I2]equil = 2.00 – x = 2.00 – 1.37 = 0.63 M [HI]equil = 2.00 + 2x = 2.00 + 2(1.37) = 2.00 + 2.74 = 4.74 M Chemistry: The Molecular Nature of Matter, 6E 70 Your Turn! N2(g) + O2(g) → 2NO(g) Kc = 0.0123 at 3900 oC If 0.25 moles of N2 and O2 are placed in a 250 mL container, what are the equilibrium concentrations of all species ? A. 0.0526 M, 0.947 M, 0.105 M B. 0.947 M, 0.947 M, 0.105 M C. 0.947 M 0.105 M, 0.0526 M D. 0.105 M, 0.105 M, 0.947 M Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 71 Your Turn! - Solution Conc (M) Initial Change Equil N2(g) +O2(g) 1.00 1.00 –x –x 1.00 – x 1.00 – x 2NO (g) 0.00 + 2x + 2x 0.250 mol [N2 ] [O2 ] 1.00M 0.250 L (2x )2 2x 0.0123 0.0123 2 1x (1 x ) x 0.0526M Jespersen/Brady/Hyslop [NO] = 2x = 0.105M Chemistry: The Molecular Nature of Matter, 6E 72 Calculate [X]equilibrium from [X]initial and KC Ex. 6 CH3CO2H(aq) + C2H5OH(aq) acetic acid ethanol CH3CO2C2H5(aq) + ethyl acetate H2O(l) KC = 0.11 An aqueous solution of ethanol and acetic acid, each with initial concentration of 0.810 M, is heated at 100 °C. What are the concentrations of acetic acid, ethanol and ethyl acetate at equilibrium? Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 73 Calculate [X]equilibrium from [X]initial and KC When KC is very small Ex. 7 2H2O(g) 2H2(g) + O2(g) At 1000 °C, KC = 7.3 10–18 If the initial H2O concentration is 0.100M, what will the H2 concentration be at equilibrium? Step 1. Write Equilibrium Law Kc [H2 ]2 [O 2 ] 2 [H2 O] Jespersen/Brady/Hyslop 7.3 10 18 Chemistry: The Molecular Nature of Matter, 6E 74 Ex. 7 Step 2. Concentration Table Conc (M) 2H2O(g) Initial 0.100 Change – 2x Equil’m 0.100 – 2x 7.3 10 18 2H2(g) + O2(g) 0.00 0.00 +2x +x +x +2x (2x )2 x 2 (0.100 2x ) 4x 3 (0.100 2x )2 Cubic equation – tough to solve Make approximation KC very small, so x will be very small Assume we can neglect x must prove valid later Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 75 Ex. 7 Step 3. Solve for x Assume (0.100 – 2x) 0.100 Conc (M) 2H2O (g) 2H2 (g) + O2 (g) Initial Change Equil’m 0.100 0.00 0.00 – 2x +2x 0.100 +2x +x +x Now our equilibrium expression simplifies to 2 3 (2x ) x 4x 18 7.3 10 (0.100)2 0.010 4x 3 0.010(7.3 10 18 ) = 7.3 × 10–20 Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 76 Ex. 7 Step 3. Solve for x 20 7 . 3 10 x3 1.8 10 20 4 Now take cubic root 3 x 1.8 10 20 2.6 10 7 x is very small 0.100 – 2(2.610–7) = 0.09999948 Which rounds to 0.100 (3 decimal places) [H2] = 2x = 2(2.610–7) = 5.210–7 M Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 77 Simplifications: When Can You Ignore x in Binomial (Ci – x)? If equilibrium law gives very complicated mathematical problems And if K is small Change to reach equilibrium (x term) is also small Compare initial concentration Ci in binomial to value of K Ci 400 K Use proof to show that dropped x term was sufficiently small dropped x term ? 0.05 Ci Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 78 Learning Check For the reaction 2A(g) B(g) given that Kp = 3.5×10–16 at 25°C, and we place 0.2 atm A into the container, what will be the pressure of B at equilibrium? PN2O4 Q 2A ↔ B 2 PNO I C E 0.2 0 atm x 16 –2x +x 3.5 10 2 ( 0 . 2 ) 0.2 – 2x ≈0.2 x –17 0 x = 1.4×10 Q 0 2 (0.2) [B]= 1.4×10–17 M Q K shifts right proof: 1.4×10–17/0.2<0.05 Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 79 Your Turn! In the reaction shown, K = 1.8 × 10–5 HC2H3O2(aq) + H2O(l) ↔ H3O+(aq) + C2H3O2–(aq) If we start with 0.3M HC2H3O2, what will be the equilibrium concentration of C2H3O2 –? A. 0.3 M B. 0.002 M C. 0.04 M D. 0.5 M Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 80 Calculating KC Given Initial Concentrations and One Final Concentration Ex. 2a H2(g) + I2(g) 2HI(g) @ 450 °C Initially H2 and I2 concentrations are 0.200 mol each in 2.00L (= 0.100M); no HI is present At equilibrium, HI concentration is 0.160 M Calculate KC To do this we need to know 3 sets of concentrations: initial, change and equilibrium Jespersen/Brady/Hyslop Chemistry: The Molecular Nature of Matter, 6E 81