* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Unit 11 GHP
Rook polynomial wikipedia , lookup
Eigenvalues and eigenvectors wikipedia , lookup
Dessin d'enfant wikipedia , lookup
Quadratic equation wikipedia , lookup
Gröbner basis wikipedia , lookup
Cubic function wikipedia , lookup
Polynomial greatest common divisor wikipedia , lookup
Root of unity wikipedia , lookup
Horner's method wikipedia , lookup
Cayley–Hamilton theorem wikipedia , lookup
Quartic function wikipedia , lookup
Factorization of polynomials over finite fields wikipedia , lookup
Polynomial ring wikipedia , lookup
System of polynomial equations wikipedia , lookup
Eisenstein's criterion wikipedia , lookup
Remainder and Factor
Theorems
Unit 11
Definitions
The real number, r, is a zero of f(x) iff:
r is a solution, or root, of f(x)=0
x-r is a factor of the expression that
defines f (f(r)=0)
when the expression is divided by xr, the remainder is 0
r is an x-intercept of the graph of f.
Remainder Theorem
If the polynomial expression that
defines the function of P is divided by
x-r, then the remainder is the number
P(r).
Factor Theorem
x-r is a factor of the polynomial
expression that defines the function P
iff r is a solution of P(x)=0. That is, if
P(r)=0.
Integer Roots
Unit 11
Page 464, #42-44
42)
43)
44)
Warm Up
Find the polynomial P(x) in the standard
form that has roots of x = {-3, -1, 1}
and P(0) = 9.
Quiz
Factor & Remainder Theorem
.
Example
As the first step in creating a graph of the
polynomial, find all x-intercepts of the
polynomial:
.
Rational Root Theorem
Let P be a polynomial function with integer
coefficients in standard form. If
is a
root of P(x) = 0, then
p is a factor of the constant term of P and
q is a factor of the leading coefficient of P.
Determine the number of roots.
List all factors of the constant term.
List all factors of the leading coefficient.
List all the possible roots.
Test each possible root to find the zeros of each
polynomial.
Examples
1.)
2.)
Examples
3.)
4.)
Assignment
Worksheet #1, 1-5
Show What You Know
Rational Roots
Unit 11
Warm Up
List all possible roots and use them to
find the zeros of the polynomial:
Worksheet #1, 1-5
1)
2)
3)
4)
5)
-6, -1, 1
-3, -2, 2
-4, 2 (multiplicity 2)
-1 (multiplicity 2), 2
-3, -1, 2, 3
Rational Root Theorem
Let P be a polynomial function with integer
coefficients in standard form. If
is a
root of P(x) = 0, then
p is a factor of the constant term of P and
q is a factor of the leading coefficient of P.
Determine the number of roots.
List all factors of the constant term.
List all factors of the leading coefficient.
List all the possible roots.
Test each possible root (using substitution or
synthetic division) to find the zeros of each
polynomial.
Examples
1.)
2.)
Assignment
Worksheet #2, 1-16
Show What You Know
Rational Roots
Unit 11
Warm Up
List all possible roots and use them to
find the zeros of the polynomial:
Worksheet #2, 1-16
1)
2)
3)
4)
5)
6)
7)
8)
1,
1,
1,
1,
1,
1,
1,
1,
1/3
2, 4, 8, 16, 32, 64
2, 5, 10
2, 4, 8, 1/5, 2/5, 4/5, 8/5
5, 25, ½, 5/2, 25/2, ¼, 5/4, 25/4
3, 7, 21, 1/5, 3/5, 7/5, 21/5
3, 9, 27
7, ½, 7/2
Worksheet #2, 1-16
9) x={1 (multiplicity 2), -3}
10) x={1 (multiplicity 2), 11}
11) x={-1 (multiplicity 2), -2}
12) x={-1, 1/5, -5}
13) x={1 (multiplicity 2), ¼}
14) x={-1, 1/3, -3}
15) x={1 (multiplicity 2), 1/5, 7}
16) x={-1 (multiplicity 2), 1/3, 5}
Quiz
Integer and Rational Roots
Graphing Polynomials
Unit 11
Warm Up
Determine the number of roots. Then find the
roots of the polynomial.
Critical Thinking
In the process of solving
you test 1, 2, 5, and 10 as possible zeros and
determine that none of them are actual zeros.
You then discover that -5/2 is a zero. You
calculate the depressed polynomial to be
Do you need to test 1, 2, 5, and 10 again?
Why or why not?
End Behavior
What happens to a
polynomial
function as its xvalues get very
small and very
large is called the
end behavior of
the function.
End Behavior
f(x)=axn+…
a>0
a<0
left right left right
n is even
n is odd
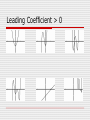
Leading Coefficient > 0
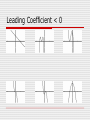
Leading Coefficient < 0
End Behavior
f(x)=axn+…
a>0
a<0
left right left right
n is even
increase
decrease
n is odd
increase
decrease
Highest Exponent is Odd
Highest Exponent is Even
End Behavior
f(x)=axn+…
a>0
a<0
left right left right
n is even increase
increase decrease decrease
n is odd decrease increase
increase decrease
Examples
Sketch the graph of each polynomial.
1.)
2.)
3.)
Assignment
Worksheet 3, #1-8
Exit Survey
Which of the following is the graph of
B.
?
A.
B.
C.
D.
Polynomial Review
Unit 11
Warm Up
Sketch a graph of the polynomial:
2x 2x 16x 24
3
2
Example #1
A=True
B=False
a) If f(-5)=0, then (x-5) is a factor of f(x).
b) If x=9 is a root of f(x), then (x-9) is a
factor of f(x).
c) If the polynomial f(x) is synthetically
divided by (x-4) and the remainder is 0,
then f(4)=0.
Example #2
Determine if (x+1) is a factor of
3
2
the polynomial: 2x 3x x 6
A=Yes
B=No
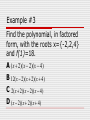
Example #3
Find the polynomial, in factored
form, with the roots x={-2,2,4}
and f(1)=18.
A (x 2)(x 2)(x 4)
B 12(x 2)(x 2)(x 4)
C 2(x 2)(x 2)(x 4)
D (x 2)(x 2)(x 4)
Example #4
2x 13x 17x 12
3
2
•How many roots will the function have?
•List all the possible rational roots.
•Perform the synthetic division.
•Write the polynomial in its factored form with
each factor having only integer coefficients.
•Write the roots of the polynomial.
•Sketch the graph.
Assignment
Review Sheet