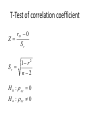* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture Slides
Sufficient statistic wikipedia , lookup
Psychometrics wikipedia , lookup
Foundations of statistics wikipedia , lookup
Bootstrapping (statistics) wikipedia , lookup
History of statistics wikipedia , lookup
Taylor's law wikipedia , lookup
Gibbs sampling wikipedia , lookup
Misuse of statistics wikipedia , lookup
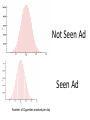
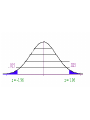
Inferential Statistics Coin Flip • How many heads in a row would it take to convince you the coin is unfair? • 1? • 10? Number of Tosses Approx Probability of All Heads 1 (½)1=.5 2 (½)2=.25 3 (½)3=.125 4 (½)4=.063 5 (½)5=.031 6 (½)6=.016 7 (½)7=.008 8 (½)8=.004 9 (½)9=.002 10 (½)10=.001 100 (½)100=7.88-e31 Not Seen Ad Seen Ad Number of Cigarettes smoked per day Inferential Statistics • To draw inference from a sample about the properties of a population • Population distribution: The distribution of a given variable(parameter) for the entire population • Sample distribution: A sample of size n, is drawn from the population and the variable’s distribution is called the sample distribution. • Sampling distribution: This refers to the properties of a particular test statistic. The sampling distribution draws the distribution of the test statistic if it were calculated from a sample of size n, then resample using n observation to calculate another test statistic. Collect these into the sampling distribution. • http://onlinestatbook.com/stat_sim/sampling _dist/index.html • Law of Large Numbers and Central Limit Theorem • How can we use this information? We can use our knowledge of the sampling distribution of a test statistic, a single realization of that test statistic to infer the probability that it came from a certain population One Sample T-test of mean x Z Sx • • • If the calculate Z statistic is large than the critical value (C.L.) then we reject the null hypothesis, we can also use p-values. That is the exactly probability of drawing a this sample from a population as is hypothesized under the null distribution. If the p-value is large (generally larger than .05 (5%)), we fail to reject the null, if it is small we reject the null. Z distribution (standard normal) vs. t-distribution (students t) The t distribution is used in situations where the population variance is unknown and the sample size is less than 30. Hypothesis testing • Develop a hypothesis about the population, then ask does the data in our sample support the hypothesized population characteristic. • Ho: Null hypothesis • Ha: Alternative hypothesis • Significance level. The a critical point where the probability of realizing this sample when pulled from a population as hypothesized under the under the • Type I and II Errors (Innocent until proven Guilty) • What if Ho = innocent State of Ho in pop Ho is true Ho is false Accept Ho Correct Type II error Reject Ho Type I error Correct • alpha = the nominal size of the test (probability of a type I error) • Beta = probability of a type II error • 1-beta= the power of a test (ability to reject a false null) Confidence Intervals • Confidence intervals for the mean/proportion CI x Z C.L. S x Where Z C.L. is the appropriate std. normal value for the associate confidence level. 95% C.L. = 1.96 99% C.L. = 2.57 90% C.L. = 1.65 and Sx S the standard error of the mean (based on the C.L.T) n The population mean lies within the range. Z(T-Test) of proportion p Z Sp where Sp p(1 p) n • Example: – Males represent 47.9% of the population over the age of 18. Ho: Ha: .479 .479 Categorical/Categorical • Crosstabulations (2 way frequency tables, Crosstabs, Bivariate distributions) Smoke\Gender Male Female Row total Yes 30 25 55 No 20 25 45 column total 50 50 100 Chi-squared test of independence • categorical/categorical 2 O ij Eij 2 Eij • with degrees of freedom (R-1)(C-1) where R = number of rows and C= number of columns Ri C j Eij n Smoke\Gender Male Female Row total Yes 30 (27.5) 25 (27.5) 55 No 20 (22.5) 25 (22.5) 45 column total 50 50 100 • χ2=1.01 and the critical value with 1 degree of freedom at the 5% level is 3.84 fail to reject • H0: The variables are independent, that is to say knowledge of one will not help to predict the outcome of the other HOW OFTEN DOES R READ NEWSPAPER * RESPONDENTS SEX Crosstabulation HOW OFTEN DOES R READ NEWSPAPER EVERYDAY FEW TIMES A WEEK ONCE A WEEK LESS THAN ONCE WK NEVER Total Count Expected Count Count Expected Count Count Expected Count Count Expected Count Count Expected Count Count Expected Count RESPONDENTS SEX MALE FEMALE 208 221 189.2 239.8 97 129 99.7 126.3 79 98 78.1 98.9 37 62 43.7 55.3 24 54 34.4 43.6 445 564 445.0 564.0 Chi-Square Tests Pearson Chi-Square Value 10.933 a df 4 As ymp. Sig. (2-sided) .027 a. 0 cells (.0%) have expected count less than 5. The minimum expected count is 34.40. Total 429 429.0 226 226.0 177 177.0 99 99.0 78 78.0 1009 1009.0 Categorical/Continuous • Any statistic that applied to cont. variables done for each category – Mean, median, mode. – Variance, Std dev, skewness, kurtosis Comparison of Means • Z test (T-test) comparison of means. Null hypothesis is that the mean difference is 0 x1 x 2 Z S x1 x2 H 0 : 1 2 0; 1 2 H a : 1 2 0; 1 2 • Where S is the pooled estimate of the standard error of the mean, assuming the underlying population variances are equal. x1 x 2 S x1 x2 S S12 S 22 n1 n2 n1 1S12 n2 1S 22 n1 1 n2 1 • Pooled estimate of the standard error (population variances equal) Group Statistics how often r reads news AGE OF RESPONDENT 1 Never 0 At Least less than once a week Std. Error Mean Std. Deviation Mean 46.31 20.512 2.323 N 78 931 45.73 17.001 .557 Independent Samples Test t-test for Equality of Means t AGE OF RESPONDENT Equal variances assumed df .286 1007 Sig. (2-tailed) Mean Difference Std. Error Difference .775 .583 2.039 95% Confidence Interval of the Difference Lower Upper -3.418 4.583 Continuous/Continuous • Simple Correlation coefficient (Pearson’s product-moment correlation coefficient, Covariance) rxy ryx ( x x )( y y ) ( x x ) ( y y) i i 2 i • this ranges from +1 to -1 i 2 T-Test of correlation coefficient Z Sr rxy 0 Sr 1 r2 n2 H 0 : xy 0 H a : xy 0 Four sets of data with the same correlation of 0.816