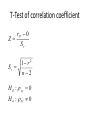Download Lecture Slides

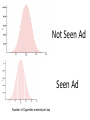
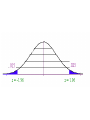
Inferential Statistics
Coin Flip
• How many heads in a row would it take to
convince you the coin is unfair?
• 1?
• 10?
Number of Tosses
Approx Probability of All Heads
1
(½)1=.5
2
(½)2=.25
3
(½)3=.125
4
(½)4=.063
5
(½)5=.031
6
(½)6=.016
7
(½)7=.008
8
(½)8=.004
9
(½)9=.002
10
(½)10=.001
100
(½)100=7.88-e31
Not Seen Ad
Seen Ad
Number of Cigarettes smoked per day
Inferential Statistics
• To draw inference from a sample about the properties of a
population
• Population distribution: The distribution of a given
variable(parameter) for the entire population
• Sample distribution: A sample of size n, is drawn from the
population and the variable’s distribution is called the sample
distribution.
• Sampling distribution: This refers to the properties of a particular
test statistic. The sampling distribution draws the distribution of
the test statistic if it were calculated from a sample of size n, then
resample using n observation to calculate another test statistic.
Collect these into the sampling distribution.
• http://onlinestatbook.com/stat_sim/sampling
_dist/index.html
• Law of Large Numbers and Central Limit
Theorem
• How can we use this information? We can use
our knowledge of the sampling distribution of
a test statistic, a single realization of that test
statistic to infer the probability that it came
from a certain population
One Sample T-test of mean
x
Z
Sx
•
•
•
If the calculate Z statistic is large than the critical value (C.L.) then we reject the
null hypothesis, we can also use p-values. That is the exactly probability of
drawing a this sample from a population as is hypothesized under the null
distribution. If the p-value is large (generally larger than .05 (5%)), we fail to reject
the null, if it is small we reject the null.
Z distribution (standard normal) vs. t-distribution (students t)
The t distribution is used in situations where the population variance is unknown
and the sample size is less than 30.
Hypothesis testing
• Develop a hypothesis about the population, then ask
does the data in our sample support the hypothesized
population characteristic.
• Ho: Null hypothesis
• Ha: Alternative hypothesis
• Significance level. The a critical point where the
probability of realizing this sample when pulled from a
population as hypothesized under the under the
• Type I and II Errors (Innocent until proven Guilty)
• What if Ho = innocent
State of Ho in pop
Ho is true
Ho is false
Accept Ho
Correct
Type II error
Reject Ho
Type I error
Correct
• alpha = the nominal size of the test (probability of a
type I error)
• Beta = probability of a type II error
• 1-beta= the power of a test (ability to reject a false
null)
Confidence Intervals
• Confidence intervals for the mean/proportion
CI  x  Z C.L. S x
Where
Z C.L. is the appropriate std. normal value for the associate confidence level.
95% C.L. = 1.96
99% C.L. = 2.57
90% C.L. = 1.65
and
Sx 
S
the standard error of the mean (based on the C.L.T)
n
The population mean lies within the range.
Z(T-Test) of proportion
p 
Z
Sp
where
Sp 
p(1  p)
n
• Example:
– Males represent 47.9% of the population over the
age of 18.
Ho: 
Ha: 
 .479
 .479
Categorical/Categorical
• Crosstabulations (2 way frequency tables,
Crosstabs, Bivariate distributions)
Smoke\Gender
Male
Female
Row total
Yes
30
25
55
No
20
25
45
column total
50
50
100
Chi-squared test of independence
• categorical/categorical
2  
O
ij
 Eij 
2
Eij
• with degrees of freedom (R-1)(C-1) where R =
number of rows and C= number of columns
Ri C j
Eij 
n
Smoke\Gender
Male
Female
Row total
Yes
30 (27.5)
25 (27.5)
55
No
20 (22.5)
25 (22.5)
45
column total
50
50
100
• χ2=1.01 and the critical value with 1 degree of
freedom at the 5% level is 3.84 fail to reject
• H0: The variables are independent, that is to say
knowledge of one will not help to predict the
outcome of the other
HOW OFTEN DOES R READ NEWSPAPER * RESPONDENTS SEX Crosstabulation
HOW OFTEN DOES
R READ
NEWSPAPER
EVERYDAY
FEW TIMES A WEEK
ONCE A WEEK
LESS THAN ONCE WK
NEVER
Total
Count
Expected Count
Count
Expected Count
Count
Expected Count
Count
Expected Count
Count
Expected Count
Count
Expected Count
RESPONDENTS SEX
MALE
FEMALE
208
221
189.2
239.8
97
129
99.7
126.3
79
98
78.1
98.9
37
62
43.7
55.3
24
54
34.4
43.6
445
564
445.0
564.0
Chi-Square Tests
Pearson Chi-Square
Value
10.933 a
df
4
As ymp. Sig.
(2-sided)
.027
a. 0 cells (.0%) have expected count less than 5. The
minimum expected count is 34.40.
Total
429
429.0
226
226.0
177
177.0
99
99.0
78
78.0
1009
1009.0
Categorical/Continuous
• Any statistic that applied to cont. variables
done for each category
– Mean, median, mode.
– Variance, Std dev, skewness, kurtosis
Comparison of Means
• Z test (T-test) comparison of means. Null
hypothesis is that the mean difference is 0
x1  x 2
Z
S x1  x2
H 0 : 1   2  0; 1   2
H a : 1   2  0; 1   2
• Where S is the pooled estimate of the
standard error of the mean, assuming the
underlying population variances are equal.
x1  x 2
S x1  x2 
S 
S12 S 22

n1 n2
n1  1S12  n2  1S 22
n1  1  n2  1
• Pooled estimate of the standard error
(population variances equal)
Group Statistics
how often r reads news
AGE OF RESPONDENT 1 Never
0 At Least less than
once a week
Std. Error
Mean Std. Deviation Mean
46.31
20.512
2.323
N
78
931
45.73
17.001
.557
Independent Samples Test
t-test for Equality of Means
t
AGE OF RESPONDENT Equal variances
assumed
df
.286
1007
Sig. (2-tailed)
Mean
Difference
Std. Error
Difference
.775
.583
2.039
95% Confidence
Interval of the
Difference
Lower
Upper
-3.418
4.583
Continuous/Continuous
• Simple Correlation coefficient (Pearson’s
product-moment correlation coefficient,
Covariance)
rxy  ryx 
 ( x  x )( y  y )
 ( x  x )  ( y  y)
i
i
2
i
• this ranges from +1 to -1
i
2
T-Test of correlation coefficient
Z 
Sr 
rxy  0
Sr
1 r2
n2
H 0 :  xy  0
H a :  xy  0
Four sets of data with the same correlation of 0.816