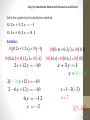Download 8.2 Solving Systems of Linear Equations by Substitution

8.2 Solving Systems
of Linear Equations
by Substitution
Objective 1
Solve linear systems by substitution.
Slide 8.2-3
Solve linear systems by substitution.
Graphing to solve a system of equations has a serious drawback. It is difficult
5
1
,


to find an accurate solution, such as  3 6  ,from a graph. One algebraic
method for solving a system of equations is the substitution method.
This method is particularly useful for solving systems in which one equation
is already solved, or can be solved quickly, for one of the variables.
Slide 8.2-4
CLASSROOM
EXAMPLE 1
Using the Substitution Method
Solve the system by the substitution method.
2 x  7 y  12
x  2 y
Solution:
2  2 y   7 y  12
4 y  7 y  12
3 y 1 2

3
3
y  4
x  2 y
x  2  4
x 8
8, 4
The solution set found by the substitution method will be the same as the
solution found by graphing. The solution set is the same; only the method is
different. A system is not completely solved until values for both x and y are
found.
Slide 8.2-5
CLASSROOM
EXAMPLE 2
Using the Substitution Method
Solve the system by the substitution method.
2 x  7 y  12
x  3 2y
Solution:
2  3  2 y   7 y  12
6  4 y  7 y  12
6  3 y  6  12  6
3 y 1 8

3
3
y  6
x  3  2  6
x  3 12
x  15
15, 6
Be careful when you write the ordered-pair solution of a system. Even though we found y
first, the x-coordinate is always written first in the ordered pair.
Slide 8.2-6
Solve linear systems by substitution. (cont’d)
Solving a Linear System by Substitution
Step 1: Solve one equation for either variable. If one of the
variables
has coefficient 1 or −1, choose it, since it usually makes the
substitution method easier.
Step 2: Substitute for that variable in the other equation. The
should be an equation with just one variable.
result
Step 3: Solve the equation from Step 2.
Step 4: Substitute the result from Step 3 into the equation
to find the value of the other variable.
from Step 1
Step 5: Check the solution in both of the original equations. Then write the
solution set.
Slide 8.2-7
CLASSROOM
EXAMPLE 3
Using the Substitution Method
Use substitution to solve the system.
x  1  4 y
2 x  5 y  11
Solution:
x  1  1  4 y  1
x  4 y  1
x  4  1 1
x  4 1
x 3
2  4 y 1  5 y  11
8 y  2  5 y  2  11  2
13 y 13

13 13
y  1
3, 1
Slide 8.2-8
Objective 2
Solve special systems by substitution.
Slide 8.2-9
Solve special systems by substitution.
Recall from Section 8.1 that systems of equations with graphs that are
parallel lines have no solution. Systems of equations with graphs that are the
same line have an infinite number of solutions.
Slide 8.2-10
CLASSROOM
EXAMPLE 4
Solving an Inconsistent System by Substitution
Use substitution to solve the system.
y  8x  4
16 x  2 y  8
Solution:
16 x  2 8x  4  8
16x 16x  8  8
8  8
Since the statement is false, the solution set is Ø.
It is a common error to give “false” as the solution of an inconsistent system. The
correct response is Ø.
Slide 8.2-11
CLASSROOM
EXAMPLE 5
Solving a System with Dependent Equations by Substitution
Solve the system by the substitution method.
x  3 y  7
4 x  12 y  28
Solution:
x  3 y  3 y  7  3 y
x  7  3 y
4  7  3 y   12 y  28
28  12 y  12 y  28
28  28
Since the statement is true every solution of one equations is also
a solution to the other, so the system has an infinite number of
solutions and the solution set is {(x,y)|x + 3y = −7}.
It is a common error to give “true” as the solution of a system of dependent
equations. Remember to give the solution set in set-builder notation using the
equation in the system that is in standard form with integer coefficients that have
no common factor (except 1).
Slide 8.2-12
Objective 3
Solve linear systems with fractions and
decimals by substitution.
Slide 8.2-13
CLASSROOM
EXAMPLE 6
Using the Substitution Method with Fractions as Coefficients
Solve the system by the substitution method.
1
1
1
x
y 
2
3
3
1
x  2 y  2
2
1 
1
1
 6  x  y     6
3 
3
2
3 x  2 y  2
3  4  4 y   2 y  2
Solution:
12  12 y  2 y  12  2  12
1

2
x

2
y
 
10 y
10
  2  2 
2



10
10
x  4 y  4 y  4  4 y
y  1
x  4  4 y
x  4  4  1
x  4  4
x0
 0, 1
Slide 8.2-14
CLASSROOM
EXAMPLE 7
Using the Substitution Method with Decimals as Coefficients
Solve the system by the substitution method.
0.2 x  1.2 y  1
0.1x  0.3 y  0.1
Solution:
10  0.2 x  1.2 y   10  1
10  0.2 x   10 1.2 y   10  1
2 x  12 y  10
2(1  3 y )  12 y  10
2  6 y  12 y  10
6 y  12
y  2
10  0.1x  0.3 y   10  0.1
10  0.1x   10  0.3 y   10 .01
x  3y  1
x  1 3y
x  1  3  2 
x7
 7, 2
Slide 8.2-15